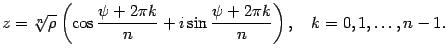СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ:

5) Умножение комплексных чисел.Свойства умножения.Деление.

Умножение комплексных чисел.

Определеие произведения комплексных чисел устанавливается с таким расчетом, чтобы числа a + b·i и a′ + b′·i можно было перемножать как алгебраические двухчлены, и чтобы число i обладало свойством i^2=−1. Произведение комплексных чисел a + b·i, и a′ + b′·i равно:

(a+bi)·(a′+b′i) = (a·a′−b·b′)+(a·b′+b·a′)i.

Деление комплексных чисел.

Устанавливается следующее определение. Разделить комплексное число a + b·i (делимое) на комплексное число a′ + b′·i (делитель) - значит найти такое число x + y·i (частное), которое, будучи помножено на делитель, даст делимое.

Если делитель не равен нулю, то деление всегда возможно и частное единственно.

Частное комплексных чисел a + b·i, и a′ + b′·i вычисляется по формуле:

a+b·i/a′+b′·i = a·a′−b·b′/a′^2+b′^2 + (a′·b−b′·a)*i/a′^2+b′^2.

6)Решение уравнения .

Мнимая единица — комплексное число, квадрат которого равен отрицательной единице.

В математике мнимая единица обозначается как латинская i или j. Она позволяет расширить поле вещественных чисел до поля комплексных чисел. Точное определение зависит от способа этого расширения.

Основной причиной введения мнимой единицы является то, что не каждое уравнение f(x) = 0 с вещественными коэффициентами имеет решения в поле вещественных чисел. Например, уравнение не имеет вещественных корней. Однако если предположить, что корнями являются комплексные числа, тогда это уравнение, как и любое другое уравнение, имеет решение.

Утверждение о том, что мнимая единица — это «квадратный корень из −1», не совсем корректно, т.к. −1 имеет два арифметических квадратных корня, один из которых можно обозначить как i, а другой как − i. Какой именно корень принимать за мнимую единицу — неважно, все математические равенства сохраняют свою силу при одновременной замене всех i на − i и − i на i.

Мнимая единица — число, квадрат которого равен −1. Таким образом i — это решение уравнения или

Если мы определим i таким образом и будем считать ее неизвестной («воображаемой», «мнимой») переменной, тогда вторым решением уравнения будет − i, что можно проверить подстановкой.

7)ГЕОМЕТРИЧЕСКАЯ ИНТЕРПЕРТАЦИЯ КОМПЛ. 4ИСЕЛ.

Сложение и вычитание.

Сложение и вычитание двух комплексных чисел определяются таким способом:

то есть надо сложить (или вычесть) отдельно вещественные и мнимые части чисел:

.

Умножение.

Умножение двух комплексных чисел производится как умножение обычных чисел, надо лишь помнить, что :

8) Деление.

Для деления комплексных чисел полезно запомнить следующее правило: чтобы разделить два комплексных числа друг на друга надо числитель и знаменатель умножить на число, комплексно сопряженное знаменателю. Тогда легко получить, что

.

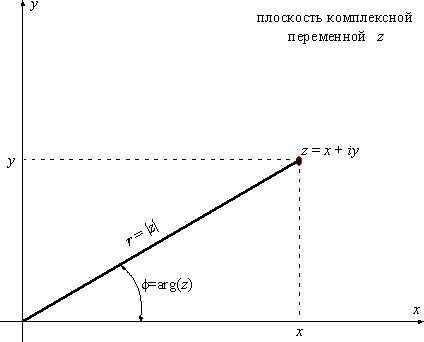
9) Пусть имеется комплексное число . Возьмем на плоскости декартову систему координат и комплексному числу z поставим в соответствие точку на этой плоскости с координатами (x, y). Таким образом, геометрически комплексные числа – это точки на плоскости. Саму плоскость называют плоскостью комплексной переменной z.

10) Нера́венство треуго́льника - это одно из свойств расстояния. Оно утверждает, что длина любой стороны треугольника всегда не превосходит сумму длин двух его других сторон. Неравенство треугольника включается как аксиома в определение нормы(нормированного пространства).

Пусть - нормированное векторное пространство, где X — произвольное множество, а — определённая на X норма. Тогда по определению последней справедливо:

Нормированным векторным пространством называется пара , где V — векторное пространство, а норма в V.

Норма — функция, заданная на векторном пространстве и обобщающая понятие длины вектора или абсолютного значения числа.

Извлечение корня из комплексного числа.

Рассмотрим уравнение где неизвестным служит , а - известное комплексное число.

Если , то . Пусть . Запишем число в тригонометрической форме :

.

Здесь и - известные величины. Запишем неизвестное число в тригонометрической форме: . Здесь и - не известные. По формуле Муавра :

Таким образом ,

Если два комплексных числа равны, то их модули должны быть равны. Поэтому .В этом соотношении и - положительные числа, следовательно , где справа стоит обычный арифметический корень из положительного числа. Если два комплексных числа равны, то аргументы у них могут различаться только на величину, кратную . Поэтому

. Отсюда находим, что

В итоге получаем :