Тема 1 Общие сведения о системах и сетях электросвязи

Лекция 1.1 Основы понятия о системах электросвязи

Потребителями информации являются люди, а обмен информацией является общественной потребностью сообщества людей. Физиологические возможности человека не позволяют обеспечить непосредственную передачу больших объёмов информации на значительные расстояния без использования специальных средств, одним из видов которых являются телекоммуникационные системы. Телекоммуникационная система (система электросвязи) – это комплекс технических (аппаратно-программных) средств, обеспечивающих обмен информацией на значительных расстояниях.

Основные закономерности обмена информацией на расстоянии, её обработка, эффективная передача и помехоустойчивый приём в системах электросвязи являются предметом исследований общей теории связи. В связи с этим, задача дисциплины «Теория электрической связи» состоит в том, чтобы ознакомить студентов с современными методами анализа и синтеза систем передачи и приёма аналоговых и цифровых сигналов в условиях мешающих воздействий, а также с вопросами оптимизации телекоммуникационных систем и устройств на основе вариационных и статистических методов. В процессе изучения дисциплины студенты сталкиваются с новыми для себя понятиями, терминами и определениями.

1. Основные термины и определения

Следует оговориться, что из всех известных видов связи (почтовая, сигнальная, голубиная и т.п.) предметом изучения ТЭС является только специальный вид связи, т.е. связь с использованием электрических, оптических и электромагнитных сигналов.

В общем случае связь (communication) – это обмен информацией или посылками информации с помощью средств, функционирующих в соответствии с согласованными правилами (называемыми в конкретных условиях протоколами). Международная конвенция по электросвязи (Найроби, 1982 год) определила «электросвязь» как «...передачу, получение и приём знаков, сигналов, письменного текста, изображения и звуков или сообщений любого рода по проводной, радио и оптической или другим электромагнитным системам...». Примерно аналогичное определение электросвязи дано в «Основных положениях развития Взаимоувязанной сети связи РФ» (в настоящее время Единая сеть электросвязи РФ – ЕСЭ РФ): «Электросвязь (telecommunication) – передача или приём знаков, сигналов, текстов, изображений, звуков по проводным, оптическим или другим электромагнитным системам».

Общий принцип обмена информацией с использованием систем и сетей электросвязи иллюстрируется на рисунке 1.1.1

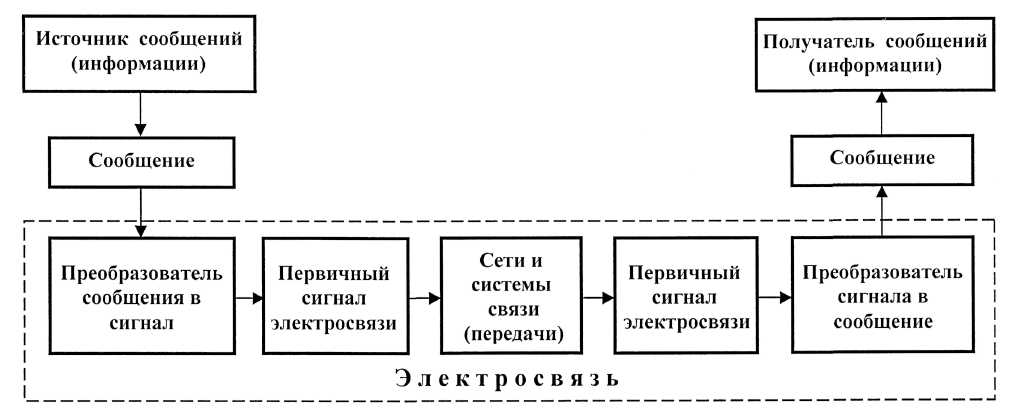
Рисунок 1.1.1 – Принцип обмена сообщений на основе систем

электросвязи

Приведенный рисунок иллюстрирует цепочку последовательных преобразований информации (объекта обмена) в сообщения и сигналы (средства обмена) и передачи последних.

Слово «информация» происходит от латинского слова informatio – разъ­яснение, ознакомление, осведомлённость. Имеется множество определений понятия информации от наиболее общего философского (информация есть отражение реального мира) до наиболее узкого практического (информация есть все сведения, являющиеся объектом хранения, передачи и преобразования). Таким образом, под информацией следует понимать не сами предметы и процессы, а их представительные характеристики, отражения или отображения в виде чисел, формул, рисунков, символов, образов и других абстрактных характеристик.

Сама по себе информация может быть отнесена к области аб­страктных категорий, подобных, например, математическим фор­мулам. Однако её хранение и передача всегда осуществляется в материально-энергетиче­ской форме.

Первым результатом преобразования информации из абстрактной категории в материально-энергетическую форму является сообщение. Всякое сообщение отображает некоторую совокупность сведений о состоянии какой-либо материальной системы, которые передаются человеком (или устройством), наблюдающим эту систему, другому человеку (или устройству), обычно не имеющему возможности получить эти сведения из непосредственных наблюдений. Эта материальная система, вместе с наблюдателем, представляет собой источник сообщения (информации). Таким образом, сообщения являются материальным носителем информации.

Представление информации в сообщении, независимо от его вида, определяет структурированную совокупность кодов (конструкцию знаков, символов или иных элементов) из определенного алфавита, которые отображают содержание передаваемого сообщения. Такие кодовые конструкции могут образовываться звуками, словами и фразами, интонацией, тембром, ритмом человеческой речи, буквами, цифрами, математическими знаками и другими элементами печатного текста, телеграммами, жестами, мимикой, изменяющимися во времени эле­ментами изображения при передаче видеоинформации и т.п. Следует отметить, что и источник и получатель информации должны пользоваться одинаковыми способами представления информации в сообщении (например, говорить на одном и том же языке, использовать один и тот же код).

Для передачи сообщения от источника получателю, независимо от величины расстояния между ними, необходимо воспользоваться каким-либо физическим процессом, который отображал бы (материализовал) информационные элементы за счет изменения некоторых своих характеристик – физических величин и обладал свойствами их наблюдения в различных точках пространства. Изменяющаяся физическая величина, например, ток в проводе, электромагнитное поле, звуковая волна и т. п., отображающая сообщение, в общем случае называется сигналом. В этом смысле естественно рассматривать сигнал как результат некоторых измерений, проводимых над физической системой в процессе её наблюдения Вид сигнала – переносчика информационных элементов сообщения в пространстве определяется видом физического процесса, используемого для материализации сообщения. Такой сигнал назовём сигналом сообщения. В зависимости от вида физического процесса сообщения могут быть:

- акустическими (речевые, музыкальные, специальные звуковые сигнальные и т.п.);

- оптическими: рукописными и машинописными (письма, телеграммы и т.п.), графическими (картины, чертежи и т.п.), визуальными (фотографии, видеоизображения и т.п.);

- телеметрическими (данные датчиков и различные сигналы управления в технических системах);

- с широким внедрением вычислительной техники получили самостоятельное значение электронные виды представления сообщений – данные.

Отображение сообщения в сигнале происходит путем изменения каких либо параметров сигнала в соответствии с изменением значений параметров структурных элементов сообщения. Так в акустическом сигнале таким параметром является мгновенное значение звукового давления на определенных частотах звукового диапазона, для изображений – коэффициент отражения в оптическом диапазоне частот и т.д.

Параметр сигнала, подвергаемый изменению в соответствии со значением структурных элементов сообщений, называют информационным параметром (ИП) сигнала сообщения.

Общая методологическая схема формирования сигнала сообщения представлена на рис.1.1.2.

Таким образом, сообщение это материальная форма представления информации для передачи её на расстояние от источника информации к получателю, определяемая способом кодирования информационных элементов и соответствующим ему видом физического процесса отображения и переноса их в пространстве.

Рисунок 1.1.2 – Методологическая схема формирования и

материализации информации

Форма сообщений, в общем случае, непосредственно не учитывает закономерности функционирования телекоммуникационных систем. Поэтому непосредственная передача сигналов сообщений по каналам электросвязи, как правило, не возможна и их необходимо тождественно преобразовать в другой сигнал, соответствующий используемым телекоммуникационным технологиям. Для этих целей в современных телекоммуникационных системах используют электрические сигналы. Как правило, поступающий от источника сигнал сообщения с помощью преобразователя сообщений преобразуется в электрический сигнал b(t), являющийся переносчиком сообщений в системах электросвязи. Этот сигнал называется первичным сигналом электросвязи. Физи­ческой величиной, определяющей такой сигнал, является ток или напряжение. Сигналы формируются путём изменения тех или иных параметров физического носителя (амплитуды, частоты или фазы сигнала или их комбинаций) в соответствии с изменением ИП сигнала передаваемого сообщения. Этот процесс изменения параметров носителя в общем случае называется модуляцией.

Сигналы и сообщения формируются и передаются во времени. Следовательно, они всегда являются функцией времени.

Параметр первичного сигнала электросвязи, изменение величины которого отображает изменение ИП сигнала сообщения, называется информационным параметром сигнала электросвязи. Значения параметров этих сигналов должны находиться в строгих пределах, определяемых соответствующими свойствами сигналов сообщения, а также стандартами и нормами электросвязи.

В большинстве случаев первичный сигнал электросвязи является комбинацией низкочастотных колебаний (сигнал тональной частоты или видеосигнал). В некоторых случаях первичные сигналы непосредственно передают по линии связи, но, как правило, они являются исходными для формирования других – высокочастотных сигналов электросвязи – специальных сигналов систем передачи, предназначенных для передачи на большие расстояния по линиям связи (кабелю или радиоканалу). Последние называются вторичными или линейными (транспортными) сигналами электросвязи. Процесс перехода от одного вида сигналов к другому должен обязательно сопровождаться модуляцией (в данном случае – параметров транспортных сигналов параметрами первичных сигналов электросвязи). В зависимости от сложности системы связи между источником и получателем сообщения такая процедура может производиться, в общем случае, неоднократно. Необходимым условием правильной доставки сообщения потребителю является попарное соответствие состава и параметров процедур модуляции и демодуляции.

1.1.2 Классификация сигналов

Сигналы электросвязи отличаются достаточно большим разнообразием, как физических свойств, так и методов описания. В общем случае те и другие взаимосвязаны. В связи с этим выбор метода описания сигналов, т. е. их математических моделей, наиболее полно учитывающих их основные физические свойствам (информационные параметры), во многом определяет качество последующих результатов анализа и синтеза телекоммуникационных систем и их отдельных элементов. Учитывая взаимосвязь методов описания и физических свойств сигналов рассмотрим их классификацию.

Сигналы классифицируются по следующим признакам.

1) По степени априорной информации.

По степени полноты априорной информации о сигнале различают детерминированные, случайные и квазидетерминированные сигналы.

Сигналы, заранее известные для любого момента времени, описываемые заданной функцией времени u(t), называются детерминированными. Детерминированные сигналы подразделяются на периодические и непериодические. Периодическим называется сигнал, удовлетворяющий условию u(t) = u(t + kT), где период Т является конечным отрезком, a k – любое целое число. Непериодическим детерминированным сигналом называется любой детерминированный сигнал, не удовлетворяющий условию u(t) = u(t + kT). Как правило, непериодический сигнал ограничен во времени.

Случайные сигналы характеризуются тем, что значения их параметров в любой момент времени заранее непредсказуемы с требуемой точностью. Случайный сигнал является частным случаем случайного процесса, представляющего изменение какой-либо случайной физической величины во времени по непредсказуемому закону. В качестве основных характеристик случайных сигналов принимают закон распределения вероятностей и спектральное распределение мощности сигнала. На основе первой характеристики можно найти относительное время пребывания величины сигнала в определенном интервале уровней, (среднее значение, мощность и ряд других важных параметров сигнала). Вторая характеристика даёт распределение средней мощности сигнала по частоте.

Наряду с полезными случайными сигналами, в теории и практике приходится иметь дело со случайными мешающими сигналами – помехами или шумами. Уровень шумов является основным фактором, ограничивающим качество и скорость передачи информации при заданном сигнале.

Разновидностью случайных сигналов являются квазидетерминированные сигналы, реализации которых описываются функциями заданного вида, но содержат один или несколько случайных параметров ..., не зависящих от времени. Реализации квазидетерминированного сигнала полностью определяются значениями случайных параметров ...

Часто встречающейся разновидностью случайных сигналов являются сигналы с медленно меняющимися случайными параметрами. В отличие от квазидетерминированных сигналов в этом случае параметры являются не случайными величинами, а случайными функциями времени, изменяющимися гораздо медленнее, чем сам сигнал при фиксированных значениях этих параметров. На коротких отрезках времени сигнал ведет себя как квазидетерминированный. При более протяжённых интервалах наблюдения его параметры должны уже рассматриваться как случайные функции времени.

В системах связи имеют дело только со случайными и квазидетерминированными сигналами.

2) По форме представления зависимости уровня от времени.

По форме представления зависимости сигнала от времени все сигналы подразделяются на три основных вида:

а) аналоговые (непрерывные сигналы непрерывного времени) – сигналы, заданные во всех точках временной оси; их реализации непрерывные функции времени (рис. 1.1.3, а);

б) дискретные:

- дискретные по уровню сигналы непрерывного времени – сигналы, заданные на дискретном множестве уровней {u_i} во всех точках временной оси (рис. 1.1.3, б);

- непрерывные по уровню сигналы дискретного времени –сигналы, заданные на дискретном множестве {t_i} точек времен­ной оси; их реализации в точках опре­деления могут принимать любое значение в пределах области его изменения (рис. 1.1.3, в);

в) дискретные сигналы дискретного времени (цифровые) – сигналы, являющиеся частным случаем дис­кретных сигналов, когда реализа­ции 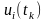в точках определения сигнала t_k принимают одно из фиксированных дискретных значений, определяемых числами с ограниченным количеством разрядов (рис. 1.1.3, г).

Рисунок 1.1.3 – Основные виды сигналов: а) непрерывный, б) дискретный по уровню непрерывного времени, в) непрерывный по уровню дискретного времени, г) дискретный по времени и уровню

Способы математического описания сигналов (сообщений и электросвязи) и их параметры определяются в ТЭС исходя из требуемых полноты и точности отображения свойств физических процессов, используемых для формирования и передачи сообщений с требуемым качеством. Поскольку все способы формирования и передачи сообщений основаны на волновых процессах распространения энергии, модели сигналов должны характеризовать взаимосвязь их частотных и энергетических свойств и закономерности их изменения во времени и в пространстве с учётом взаимодействия с техническими средствами, средой распространения и другими сигналами.

1.1.3 Основные параметры сигналов

Наиболее полным описанием конкретного сигнала, дающим представление об изменениях его формы во времени, является некоторая функция времени x(t), а о распределении его энергии по спектральным (частотным) составляющим – его спектральная функция Х(f). Однако та­кое полное описание сигнала не всегда требуется. Так количество информации, которое можно передать с помощью некоторого сигнала, зависит от его длительности, ширины спектра, мощности и некоторых других характеристик. Таким образом, для решения ряда задач достаточно более общего описания в виде нескольких параметров, характери­зующих основные свойства сигнала, важных с точки зрения его передачи и приёма. Такими параметрами являются длитель­ность сигнала Т_с, его динамический диапазон D_с и ширина спектра F_с.

Длительность сигнала T_с определяет интервал времени, в пределах которого сигнал существует.

Динамический диапазон D_с – это отношение наибольшей мгновенной мощ­ности сигнала P_{с max} к той наименьшей мощности P_{с min}, которую необходимо отличать от нуля (например, уровень шума) при заданном качестве передачи. D_с выражается обычно в децибелах:

D = 10lg(P_{с max}/P_{с min}) = 10lg(П²P_с/P_{с min}), дБ,

где П² = P_{с max}/P_с – пик-фактор сигнала по мощности,

P_с – мощность сигнала, усреднённая за достаточно большой интервал времени.

Ширина спектра сигнала F_с – диапазон частот, в пределах которого сосредоточена основная энергия сигнала. Ширина спектра сиг­нала, в принципе, может быть неограниченной. Однако для любого сигнала можно указать диапазон частот, в пределах которого сосредоточена основ­ная доля его энергия (например, более 90%). Элементы системы и линия связи имеют ограниченную полосу пропускания, поэтому спектр сигнала часто сознательно ограничивают с учётом допустимых искажений сигнала.

Весьма важной обобщенной характеристикой сигнала, позволяющей оценить трудности, связанные с его передачей, является его объём:

V_c характеризует, чаще всего, весь ансамбль используемых в данной системе связи сигналов, т. е. описывает сигнал как случайный процесс.

Наряду с объёмом сигнала используют ещё одну интегральную характеристику сигнала – базу сигнала:

В_c = 2T_cF_c.

При В_c ≤ 1 сигнал называется узкополосным, при В_с >> 1 – широкополосным.

Лекция 1.2 Системы электросвязи

1.2.1 Классификация систем электросвязи

В предыдущей лекции дано общее определение «связи» как процесса обмена информацией или посылками информации с помощью средств, функционирующих в соответствии с согласованными правилами. Совокупность технических средств и среды распространения, обеспечивающая передачу сообщений от источника к получателю, называется системой электросвязи.

При передаче сообщений системой электросвязи выполняются следующие операции:

- преобразование сообщения, поступающего от источника сообщения (ИС) в первичный сигнал электросвязи (в дальнейшем просто «первичный сигнал»);

- преобразование первичных сигналов в линейные сигналы с характеристиками, согласованными с характеристиками среды распространения (линией связи);

- выбор маршрута передачи и коммутация;

- передача сигналов по выбранному маршруту;

- преобразование сигналов в сообщение.

Обобщённая структурная схема системы электросвязи представлена на рис. 1.2.1, где приняты следующие обозначения:

ИС – источник сообщения (информации);

ПР₁ (ПР^-1) – преобразователь (обратный преобразователь) сообщения в первичный сигнал;

СК – станция коммутации, представляющая совокупность коммутационной и управляющей аппаратуры, обеспечивающей установление различного вида соединений (местные, междугородные, международные, входящие, исходящие и транзитные) и реализующей определенный метод коммутации (коммутация каналов, коммутация сообщений или коммутация пакетов);

ОС₁ (ОС^-1) – оборудование сопряжения, осуществляющее прямое (обратное) преобразование первичных сигналов в линейные сигналы (вторичные сигналы), физические характеристики которых согласуются с параметрами среды распространения (СР).

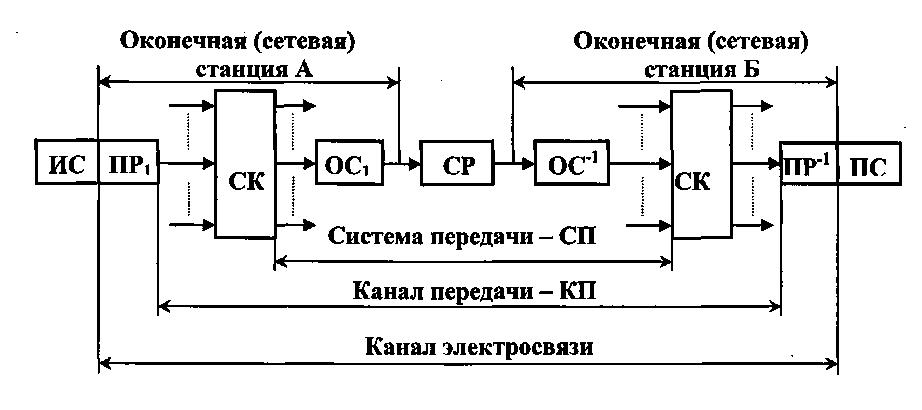
Рисунок 1.2.1 – Обобщенная структурная схема системы

электросвязи

Каналом электросвязи называется комплекс технических средств, обеспечивающий передачу сообщений между его источником и получателем. Каналу электросвязи присваивают название в зависимости от вида сети связи (телефонный, телеграфный, передачи данных). По территориальному признаку они разделяются на междугородные, зоновые и местные.

Каналом передачи называется комплекс технических средств и среды распространения, обеспечивающий передачу первичного сигнала электросвязи в определенной полосе частот или с определенной скоростью передачи между прямым и обратным преобразователем (канал передачи типовой, параметры которого соответствуют требованиям ЕСЭ РФ; тональной частоты – типовой аналоговый канал передачи с полосой частот от 0,3 до 3,4 кГц; цифровой канал основной, первичный, вторичный, третичный, четверичный).

Системой передачи называется комплекс технических средств и среды распространения, обеспечивающий передачу первич­ного сигнала в определенной полосе частот или с определен­ной скоростью передачи между коммутационными станциями.

Каналы и системы связи, использующие искусственную среду распространения (металлические провода, оптическое волокно), называются проводными или кабельными, а каналы и системы связи, в которых сигналы передаются через открытое пространство – радиоканалами и радиосистемами.

Классификация систем электросвязи весьма разнообразна, но в основном определяется видами передаваемых сообщений, сре­дой распространения сигналов электросвязи и способами распределения (коммутации) сообщений в сети (рис. 1.2.2).

Рисунок 1.2.2 – Классификация систем электросвязи по видам

передаваемых сообщений и среды распространения

По виду передавае­мых сообщений различают следующие системы связи: телефонные (передачи речи), телеграфные (передачи текста), факсимильные (передачи неподвижных изображе­ний), теле и звукового вещания (передачи подвижных изображений и звука), теле­измерения, телеуправления и передачи данных.

По назначению телефонные и телевизионные системы делятся на вещательные, отличающиеся высокой степе­нью художественности воспроизведения сообщений, и профессиональные, имеющие специальное применение (служебная связь, промышленное телеви­дение и т.п.). В системе телеизмерения измеряемая физическая величина (температура, давление, скорость и т.п.) с помощью датчиков преоб­разуется в первичный электрический сигнал, поступающий в передатчик. На приёмном конце переданную физическую величину или её изменения выделя­ют из сигнала и наблюдают или регистрируют с помощью записывающих при­боров. В системе телеуправления осуществляется передача команд для автома­тического выполнения определённых действий.

Системы передачи данных, обеспечивающие обмен информацией между вычислительными средствами и объектами автоматизированных систем управ­ления, отличаются от телеграфных более высокими скоростями и верностью передачи информации.

В зависимости от среды распространения сигналов разли­чают системы (линии) проводной связи (воздушные, кабельные, волоконно-оптиче­ские и др.) и радио­связи. Кабельные системы связи являются основой магистральных сетей дальней связи, по ним осуществля­ется передача сигналов в диапазоне частот от десятков кГц до со­тен МГц. Весьма перспективными являются волоконно-оптические линии связи (ВОЛС). Они позволяют в диапазоне от 600 до 900 ГГц (0,5...0,3 мкм) обеспечить очень большую пропускную способность (сотни телевизионных или сотни тысяч телефонных каналов). Наряду с проводными линиями связи широко используются радиолинии различных диапазонов (от сотен кГц до десятков ГГц). Эти линии более эконо­мичны и неза­менимы для связи с подвижными объектами. Наибольшее распро­странение для многоканальной радиосвязи получили радиорелей­ные линии (РРЛ) метрового, дециметрового и сантиметрового диа­пазонов на частотах от 60 МГц до 40 ГГц. Разновидностью РРЛ яв­ляют­ся тропосферные линии с использованием отражений от не­однородностей тропосферы. Всё большее применение находят спутниковые линии связи (СЛС) – РРЛ с ретранслятором на ИСЗ. Для этих линий (систем) связи отведены диапазоны частот от 4 до 6 и от 11 до 27,5 ГГц. Большая даль­ность при одном ретрансляторе на спут­нике, гибкость и возможность организации глобаль­ной связи – важные преимущества СЛС.

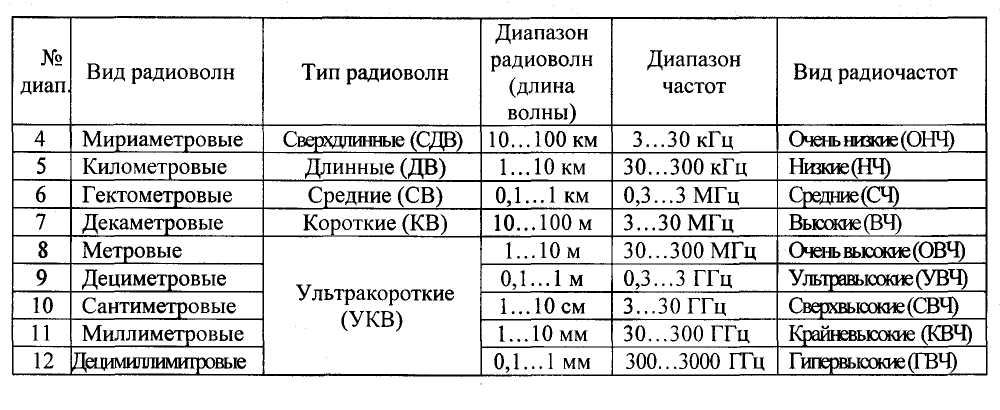
Диапазоны частот электромагнитных колебаний, используемые в системах радиосвязи, представлены в табл. 1.2.1.

Таблица 1.2.1 – Диапазон частот электромагнитных колеба­ний,

используемых в системах радиосвязи

Системы связи могут работать в одном из трёх режимов:

- симплексном – передача сооб­щений осущест­вляется в од­ном направлении от источника к полу­чателю;

- дуплекс­ном – обеспечивается возможность од­новременной передачи со­общений в прямом и обратном направлении;

- полудуплексном – обмен сообщений осуществляется пооче­редно.

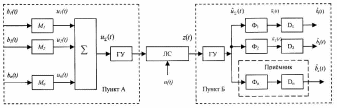
Система связи, обеспе­чивающая одновременную и независи­мую передачу нескольких сооб­щений по одной общей линии связи, называется многоканальной. Структурная схема многоканальной системы связи (МКСС) изображена на рис. 1.2.3.

Рисунок 1.2.3 – Структурная схема МКСС

Первич­ные сигналы b₁(t), b₂(t), ..., b_n(t), подлежащие передаче, преобразуются посред­ством модуляторов М₁, M₂, ..., М_п в электри­ческие сигналы u₁(t), u₂(t), …, u_n(t), а затем суммируются в аппара­туре уплотнения. Полученный таким образом групповой сигнал после усиления в групповом усилителе (ГУ) передаётся по ли­нии связи (ЛС). Приёмник из принятого коле­бания с помощью устройства разделения (фильтров Ф_i) выде­ляет инди­ви­дуальные сигналы , преобразуемые посредством демодулято­ров (детекторов) Д_i в соответствующие первичные сиг­налы 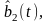…, . Для разделения сигналов на приёмном конце необхо­димо их различие между собой по некоторому признаку. В практике многоканаль­ной связи пре­имущественно применяют час­тотный и временной способы раз­де­ления.

1.2.2 Структурная схема типичной системы электросвязи

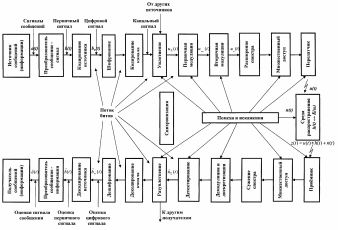
Структурная схема типичной системы связи, приведённая на рис. 1.2.4, иллюстрирует прохождение сигнала и этапы его преобразования.

Рисунок 1.2.4 – Структурная схема типичной системы связи

Верхние блоки – преобразование сообщения в сигнал, кодирование источника, шифрование, канальное кодирование, уплотнение, первичная модуляция, вторичная модуляция, расширение спектра и множественный доступ – отражают преобразования сигнала на пути от источника сообщений к передатчику. Нижние блоки – преобразование сигнала на пути от приёмника к получателю сообщений, и, по сути, они выполняют функции, взаимно противоположные верхним.

Блоки, выполняющие функции модуляции и демодуляции/детектирования, вместе называются модемом.

Для радиосистем передатчик состоит из блоков преобразования частоты в область высоких частот (радиочастот), усилителя мощности и антенны, а приёмник – из антенны и малошумящего усилителя. Обратное преобразование частоты производится на выходе приёмника или демодулятора.

Необходимыми для любой системы связи являются следующие этапы обработки: преобразование сообщения в сигнал и обратное преобразование сигнала в сообщение, модуляция, демодуляция/детектирование и, для цифровых систем связи, синхронизация.

Процедуры кодирования источника и канала, шифрования выполняются в цифровых системах связи, в которых исходные первичные сигналы первоначально преобразуются, как правило, в двоичные сигналы (биты), которые группируются затем в цифровые сообщения или символы сообщений.

Этапы преобразований сигнала, изображённые на структурной схеме, будут в дальнейшем подробно рассмотрены в данном учебном пособии.

Источ­ником и получателем сообщений в системах связи мо­жет быть человек или различного рода устройства (автомат, вычис­лительная машина и т.д.). Устройство, преобразующее сообщение в линейный сигнал, называют передающим (верхние блоки схемы), а уст­ройство, преобразующее приня­тый сигнал в сообщение, – приёмным (нижние блоки схемы).

С помо­щью первичного пре­образователя в передающем устройстве сообщение а, ко­торое может иметь любую физическую природу (изображение, звуковое коле­ба­ние и т.п.), преобразуется в первичный электрический сигнал b(t).

В передатчике первич­ный сигнал b(t) (низкочастотный) по­средством модуляции (одной или двух ступеней) превращается во вторичный (линейный высокочастот­ный) сигнал u(t), пригодный для передачи по используемому ка­налу (среде распространения).

Преобразование сообщения в сигнал должно быть обратимым, обеспечивающим возможность восстановления исходного первич­ного сигнала по выходному, т.е. получения всей информации, со­держащейся в переданном сообщении.

В системах связи среда распространения (линия связи) – это металличе­ский кабель или волновод, в системах оптической связи – это опто­волоконный кабель, в сис­темах радиосвязи – область пространства, в котором распространяются элек­тромагнитные волны от передат­чика к приёмнику.

В процессе преобразований сигнал может подвергаться искажениям и воздействию помех n(t). При­ёмное устройство обрабатывает принятый сигнал , представ­ляющий собой сумму пришедшего искажённого сигнала и помехи n(t), и восстанавли­вает по нему сообщение 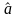, которое с некоторой погреш­ностью отображает переданное сообщение а. Приёмник на основе анализа сигнала z(t) определяет, какое из возможных сооб­щений пе­редавалось. Поэтому приёмное устройство является од­ним из наи­более ответ­ственных и сложных элементов системы связи.

Основной задачей систем электросвязи, вытекающей из данного выше определения, является передача сообщений (первичных сигналов) с требуемым качеством (в идеале – без искажений). Анализ и синтез систем связи, обеспечивающих выполнение данного требования, представляет собой достаточно сложную математическую задачу, решаемую, в общем случае, в условиях априорной неопределённости относительно параметров принимаемых сигналов и помех. В основе таких задач лежат математические модели сигналов и помех, а также систем связи и их отдельных элементов.

1.2.3 Основные характеристики систем связи

При оценке работы системы связи необходимо, прежде всего, учесть, какую точность передачи сообщения обеспечивает система и с какой скоростью передаётся информация. Первое определяет качество передачи, второе – количест­во. В реальной системе связи качество передачи зависит от степени искажений принятого сообщения. Эти искажения зависят как от свойств и технического состояния системы, так и от интенсивности и характера помех. В правильно спроектированной и технически исправной системе связи необратимые искажения сообщений обусловлены лишь воздействием помех. В этом случае качест­во передачи полностью определяется помехоустойчивостью системы.

Помехоустойчивость приёма сообщений характеризует степень соответствия переданного и принятого сообщения, выраженную в некоторой количественной мере. Помехоустойчивостью, в общем случае, называется способность системы противостоять вредному действию помех. Более конкретно помехоустойчивостью системы называется её способность сохранять показатели качества неизменными или изменяющимися лишь в допустимых пределах при действии помех. Помехоустойчивость оценивается по верности приёма сообщений при заданном отношении сигнал/помеха (ОСП) и зависит как от свойств передаваемых сигналов, так и от способа приёма. Верность приёма определяется степенью сходства принятого и переданного сообщений. В системах передачи дискретной информации в результате действия помех вместо переданной последовательности сигналов b(t) может быть принята иная последовательность . Получатель сообщения воспринимает это как появление ошибки. Поскольку появление ошибки – случайное событие, то верность передачи характеризуется вероятностью ошибки.

Если сообщение описывается непрерывной функцией a(t), то отклонение ε(t) принятого сообщения ậ(t) от переданного а(t) имеет непрерывный характер:

^(1.2.1)

и в качестве меры различия часто используется среднеквадратическое отклонение (СКО):

, (1.2.2)

где черта сверху обозначает усреднение по множеству реализаций.

При действии в канале аддитивного белого шума n(t) СКО тем меньше, чем больше отношение средней мощности сигнала к средней мощности шума (отношение сигнал/шум или сигнал/помеха – ОСШ или ОСП), т. е. при передаче непрерывных сообщений помехоустойчивость можно оценивать ОСП, а верность передачи в этом случае выражается вероятностью того, что отклонение ε(t) для всех t не превышает некоторой допустимой величины :

р[ (t) ≤ ]. (1.2.3)

Более помехоустойчивой является система, обеспечивающая большую верность приёма при заданном канале или заданную верность приёма при худшем канале.

Скоростью передачи информации R называется среднее количество информации I, передаваемое в данной системе в единицу времени:

R [дв. ед./сек.] = I/T, (1.2.4)

где Т – длительность передачи информации.

R ограничивается возможностями системы связи, т.к. при превышении R_max возрастают искажения информации, вносимые системой. К. Шенноном было показано, что значение R_max монотонно возрастает с уменьшением величины (1/n_max)ln(1/p_ош) и достигает максимального значения при (1/n_max)ln(1/p_ош) = 0, т.е. при максимально допустимом числе элементарных символов n в каждом сообщении n_max → ∞ (p_ош – вероятность ошибки воспроизведения сообщения). Это максимально достижимое значение (максимальное количество информации, которое может быть передано по каналу связи с заданной точностью за секунду) называется пропускной способностью системы С. К. Шеннон показал, что при передаче непрерывных сообщений, имеющих заданную среднюю мощность, на фоне НБШ пропускная способность системы равна:

С [дв.ед./сек.] = ∆ flog₂(1 + ), (1.2.5)

где N₀ – спектральная плотность шума; P_c – средняя мощность сигнала; ∆ f – полоса пропускания системы.

С ростом ∆ f пропускная способность системы С монотонно возрастает, стремясь при ∆ f → ∞ к пределу:

С_max[дв.ед./сек.] = 1,45 P_c/N₀. (1.2.6)

За единицу количества информации обычно принимают двоичную единицу (бит), т.е. количество информации, которое содержится в сообщении о том, что произошло одно из двух равновероятных событий.

Вероятность ошибки p_ош может быть сколь угодно малой при R ≤ C и выполнении следующих условий:

- допускаются длинные реализации сообщений (n_max → ∞), следовательно, разрешается неограниченно большая задержка их передачи;

- сообщения должны оптимально кодироваться, а принятые сигналы оптимально обрабатываться.

Своевременность передачи сообщений определяется допустимой задержкой, обусловлен­ной преобразованием сообщений и сигналов, а также конечным временем распространения сигнала по каналу связи. Она зависит, во-первых, от характера и протяжённости канала, во-вторых, от длительности обработки сигнала в передающем и приёмном устройствах. Скорость передачи и задержка являются независимыми характеристиками, практически не связанными друг с другом.

1.2.4 Основы математического моделирования систем связи

Система связи в целом и отдельные её элементы с теоретической точки зрения представляют собой сложную систему, физическое (экспериментальное) исследование которых не всегда возможно или по ряду причин не целесообразно. В связи с этим в ТЭС часто применяют математические модели, описывающие реальные элементы системы с необходимой степенью приближения. Математическая модель является основой для решения главных системо­технических задач: анализа – определения численных зна­чений показателей эффективности при заданных парамет­рах системы и характеристиках внешней среды, фиксиро­ванной структуре и алгоритме взаимодействия элементов; синтеза – выбора оптимальной структуры, алгоритмов вза­имодействия, параметров системы, оптимального управле­ния системой и др. Такая модель сводится к заданию математической модели сигналов и помех на входе и выходе канала и связей между ними.

Для полного определения решаемой в теории связи задачи необходимо задать области V_x допустимых входных воздействий и V_y допустимых выходных сигналов, ограничивающие характер входных и выходных сигналов, которые могут быть непрерывными, дискретными, цифровыми, детерминированными или случайными.

В этом случае математической моделью системы называют совокупность систем­ного оператора L, характеризующего параметры системы, и областей допустимых сигналов V_x и V_y.

Классификацию систем можно проводить на основании характерных свойств их ма­тематических моделей:

- стационарной (системой с постоянными во времени пара­метрами) называют систему, свойства которой (отклик на выходе) не зависят от момента времени поступления входного сигнала;

- нестационарной (системой с пере­менными во времени параметрами или параметрической системой) называют систему, свойства которой зависят от момента времени по­ступления входного сигнала.

Ес­ли оператор системы удовлетворяет принципу суперпозиции, то система называется линейной, в противном случае – нелинейной.

Математические модели нелинейных систем и их анализ значительно слож­нее моделей линейных систем. Одной из простейших является детерминированная безы­нер­ционная одномерная модель нелинейной системы, когда сигналы на её выходе y(t) и входе x(t) связаны соотношением:

Передача сигналов по реальным системам связи всегда сопровождается их из­менениями (преобразованиями), в результате чего принятые сигналы отличаются от переданных. Эти изменения обусловлены, прежде всего, линейными и нелинейными преобразованиями передаваемых сигналов, а также на­личием аддитивных шумов в канале. Преобразования сигнала подразделяются на обратимые (искажения) и необратимые (помехи). Обра­тимые преобразования в отличие от необратимых не влекут за собой потери информации. При необратимых преобразованиях неизбежны потери информации.

В настоящее время наиболее разработаны эффективные методы исследования линейных стационарных систем (методы преобразования Фурье и Лапласа, весовых функций – интеграла Дюамеля и др.)

Для анализа детерминированных процессов в нелинейных системах разработаны методы линеаризации, кусочно-линейной аппроксимации, гармонической линеаризации, фазовой плоскости и др.

Методы анализа случайных процессов в нелинейных системах позволяют находить законы преобразования случайных процессов при их прохождении как через безынерционные нелинейные элементы системы, так и через систему в целом, состоящую из совокупности безынерционных нелинейных и инерционных линейных элементов.

1.2.5 Методы анализа прохождения сигналов через линейные системы

Сигналы на входе линейной системы можно представить в виде суммы элементарных импульсов (временной метод анализа), а также рядами или интегралами Фурье (частотный метод анализа). Тогда алгоритм решения задачи заключается в оценке реакции системы:

- на воздействие элементарного импульса с последующим суммированием таких реакций;

- на элементарные гармонические сигналы с использованием частотных характеристик системы, указывающих закон преобразования.

а) Временной метод анализа

Пользуясь фильтрующим свойством δ-функции, входной сигнал можно представить в виде следующей динамической модели:

, (1.2.7)

показывающей ход его развития от минус ∞ до точки t. Поскольку δ(t – τ) = 0 везде, за исключением точки t = τ, то последнее выражение можно записать в следующем виде:

(1.2.8)

Импульсной характеристикой (ИХ) h(t) линейной стационарной системы называется её отклик в момент времени t на δ-импульс, по­данный в момент времени t = 0. ИХ h(t) удовлетворяет условию , где L – системный оператор. Используя ИХ отклик линейной системы на сигнал можно записать:

(1.2.9)

где оператор L «действует» лишь на величины, зависящие от текущего времени t, но не от переменной интегрирования τ.

Выражение (1.2.9) называют интегралом Дюамеля. Он определяет отклик ли­нейной стационарной системы y(t) как свёртку сигналов x(t) и h(t):

Эта формула имеет следующий физический смысл: линейная стационар­ная система выполняет операцию взвешенного сумми­рования всех мгновенных значений входного сигнала, существовавших в прошлом при - ∞ < τ < t. Роль весовой функции играет ИХ h(t).

Физически реализуемая система должна быть устойчивой: возни­кающие от внешнего воздействия δ(t) собственные колебания должны с течением времени затухать, что требует выполнения условия абсолютной ин­тегрируемости:

б) Спектральный метод анализа

Для стационарных линейных систем передаточная функция (комплексный коэффициент передачи или амплитудно-частотная характеристика – АЧХ) и ИХ связаны прямым и обратным преобразованием Фурье:

(1.2.10)

(1.2.11)

Зная спектральную плотность сигнала х(t), воздействующего на линейную систему с АЧХ , можно определить аналогичную характеристику выходного сигнала:

(1.2.12)

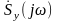где и – спектральные плотности входного и выходного сигналов, и с помощью обратного преобразования Фурье – сам вы­ходной сигнал y(t):

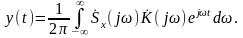(1.2.13)

Основополагающий вывод теории линейных стационарных систем – любую такую систему можно рассматривать (анализировать) как во временной области с помощью её ИХ (1.2.9), так и в частотной области, задавая передаточную функцию (АЧХ) (1.2.10, 1.2.11). При этом соотношения (1.2.12) и (1.2.13) определяют спектральный (частотный) метод анализа линейной стационарной системы, а соотношение (1.2.9) – временной метод анализа этой системы.

Лекция 1.3 Цифровое кодирование непрерывных сигналов

В настоящее время широкое применение находят цифровые системы передачи (ЦСП), в которых сигналы всех видов сообщений, в том числе и непрерывные, преобразуются в дискретные цифровые сигналы, которые затем различными способами передаются по сети.

Суть преобразования состоит в замене исходных физических сигналов последовательностью (временным рядом) кодовых слов (цифр, как правило, в двоичной системе счисления), которые отображают изменение значений исходных сигналов (или их информационных параметров) во времени. Очевидно, что для правильного восстановления сигнала сообщения на приёмном конце, такое преобразование должно быть тождественным.

Преобразование непрерывного сообщения в цифровую форму осуществляется путём последовательного выполнения операций дискретизации, квантования и кодирования.

1.3.1 Дискретизация сигналов

Дискретизация по времени выполняется путём взятия отсчётов первичного сигнала b(t) в определённые дискретные моменты t_k. В результате непрерывную функцию b(t) заменяют совокупностью мгновенных значений (отсчётов) {b(k)} или {b(t_k)} (рис. 1.3.1). Обычно моменты отсчётов выбираются на оси времени равномер­но, т.е. , где – шаг дискретизации.

Методы дискретизации сигналов можно разделить на несколько групп в зависимости от признаков классификации (рисунок 1.3.2), основными из которых являются следующие:

- регулярность отсчета;

- критерий оценки точности дискретизации и восстановления;

- базисные функции;

- принцип приближения.

, k = 1, 2, 3, … – время отсчета; = t_k – t_k-1 – шаг дискретизации

Рисунок 1.3.1 – Цифровая обработка аналогового сигнала

Рисунок 1.3.2 – Признаки, используемые при дискретизации

и восстановлении сигналов

а) Регулярность отсчетов.

В процессе дискретизации отрезок обработки сигна­ла x(t) разбивается на ряд неперекрывающихся интер­валов ∆t₁, ∆t₂, ∆t₃, _…

В соответствии с признаком регулярности отсчетов выделяются две основные группы методов дискретизации:

- равно­мерной дискретизации – длительности интервалов дискретизации ∆t_k-1= t_k – t_k-1 =∆t = const на всём отрезке обработки сигнала [-Т, Т]. Шаг дискретизации ∆t или частота дискретизации (отсчетов) f_д = выбираются на основе априорных сведений о ха­рактеристиках сигнала x(t);

- неравномерной дискретизации – длительность интервалов между отсчетами ∆t_k различ­на, ∆t_k = var.

Существует две группы неравномерных методов:

- адаптивных – интервалы ∆t_k изменя­ются в зависимости от текущего изменения параметров реализаций сигналов;

- программируемых – изменение ин­тервалов ∆t_k (частоты дискретизации f_д) производится на основе анализа поступающей информа­ции или в соответствии с заранее установленной про­граммой работы.

б) Критерий оценки точности.

Разность между истинным значением сигнала x(t) и приближающей P(t) или воспроизводящей V(t) функ­цией представляет собой текущую погрешность дискре­тизации или соответственно восстановления:

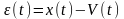. (1.3.1)

Выбор критерия оценки погрешности дискретизации (и восстановления) сигнала осуществляется получате­лем информации и зависит от целевого использования дискретизированного сигнала и возможностей аппарат­ной (программной) реализации.

1) Критерии наибольшего отклонения:

= , (1.3.2)

где – текущая погрешность, определяемая выраже­нием (1.3.1).

Правая часть этой формулы – норма функции в линейном метрическом пространстве. Расстояние между элементами такого пространства x = x(t) и v = V(t) определяется по формуле:

d(x, v)=max|x(t) - V(t)|. (1.3.3)

Эта метрика на­зывается чебышевской.

2) Среднеквадратический критерий, определяемый выражением:

, (1.3.4)

где ε(t) – текущая погрешность (1.3.2).

Черта сверху обозначает усреднение по вероятностно­му множеству. Правая часть формулы (1.3.4) – норма функции ε(t) в гильбертовом пространстве, в котором для элементов x = x(t) и v = V(t) скалярное произведение равно:

.

3) Интегральный критерий как мера отклонения x(t) от V(t) имеет вид:

.

4) Вероятностный критерий определяется соотношением:

,

где ε₀ – допустимое значение погрешности; р₀ – допус­тимая вероятность того, что погрешность не превысит значения ε₀.

в) Базисные функции.

На практике при решении задач дискретизации сиг­налов выбор типа базисных (приближающих, воспроиз­водящих) функций в основном определяется требования­ми ограничения сложности устройств (программ) ди­скретизации и восстановления сигналов.

Задачи восстановления дискретизированных сигналов в общем случае аналогичны задачам интерполирования функций. При восстановлении исходного сигнала x(t) совокупности выборок x(t_i) ставится в соответствие не­который обобщенный многочлен:

,

значения которого в точках отсчета t_k совпадают со зна­чениями функции x(t).

В классификационной таблице (рис. 1.3.2) перечис­лены основные типы функций, применяемые в задачах дискретизации и восстановления сигналов.

г) Принцип приближения.

По принципу приближения можно выделить три груп­пы методов:

- интерполяционные (определение промежуточных значений функций по ряду известных ее значений на интервале анализа);

- экстраполяционные (определение будущих значений величин на основе имеющихся данных о тенденциях их изменений в прошлые периоды);

- комбинированные (интерполяционные – экстраполяционные).

Экстраполяционные методы, не требующие задержки сиг­нала при проведении дискретизации, могут использоваться в управляющих системах, работающих в реальном времени.

Для обработки сигналов более эффективны интерпо­ляцион­ные методы, обеспечивающие меньшую избыточ­ность отсчетов по сравнению с экстраполяционными ме­тодами. Однако использова­ние интерполяционных мето­дов связано с задержкой сигнала на интервал интерполяции.

Интерполяционно – экстраполяционные методы облада­ют рядом положительных качеств, присущих как интер­поляционным, так и экстраполяционным методам. Адап­тивная дискретизация непрерывного сигнала x(t) связана с подбором приближаю­щих функций P(t) для каждого из интервалов дискре­тизации ∆t_k.

При выборе шага дискретизации рассматриваются различные модели сигналов и вводятся соответствующие критерии отбора отсчетов:

- частотный критерий, при котором интерва­лы между отсчетами выбираются с учетом частотного спектра дискретизируемого сигнала;

- корреляционный критерий отсчетов, уста­навливающий связь интервалов между отсчетами с ин­тервалов корреляции сигнала;

- квантовый критерий отсчетов, предложен­ный для детерминированной модели сигнала и устанав­ливающий зависимость интервалов между отсчетами от значения ступени квантования по уровню и крутизны (первой производной) сигнала.

1.3.2 Квантование сигналов. Импульсно-кодовая модуляция

Операция квантования заключается в передаче вместо конкретного мгновенного значения (уровня) передаваемого сообщения b(t_k) одного из ближайших значе­ний по установленной цифровой шкале дискретных уровней b_кв(t_к). Дискрет­ные значения по шкале уровней выбираются как равномерно: 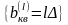, где – шаг квантования, l = 0, 1, ..., L- 1 – номер уровня квантования, так и неравномерно (рисунок 1.3.3).

а) б)

Рисунок 1.3.3 – Равномерное а) и неравномерное б) квантование сигнала

При неравномерном квантовании шаг квантования изменяется по определенному закону, увеличиваясь от минимального для слабых сигналов до максимального для сильных сигналов.

При квантовании вносится погрешность, обусловленная заменой истинного значения b(t_k) округлённым значением b_кв(t_к). Величина этой погрешности = b(t_k) – b_кв(t_k) не превосходит половины шага квантования и может быть сведена до допустимого уровня. Погрешность является случайной функцией и проявляется на выходе как дополнительный шум (шум квантования), наложенный на передаваемое сообщение. Дискретизация по времени позволяет преобразовать непрерывные сообщения в дискретный (во времени) сигнал, ко­торый после квантования и кодирования превращается в цифровой. Достоинством цифровых способов передачи является возможность применения кодов как для повыше­ния помехоустойчивости, так и для сокращения избыточности источника. В настоящее время наибольшее применение находят системы с импульсно-кодовой модуляцией (ИКМ). Импульсно-кодовой модуляцией называется преобразование отсчетов непрерывного сигнала в двоичный код. При этом непрерывное сообщение сначала подверга­ется дискретизации по времени и квантованию по уровню, а затем полученная последовательность L уровней (дискрет значений сигнала) кодируется (обычно двоичным кодом). При этом каждому уровню присваивается кодовая комбинация (число, цифра), состоящая из п символов 1 и 0.

Лекция 1.4 Преобразования сигналов в системах передачи и приёма аналоговых и дискретных сообщений

В процессе передачи исходного сообщения от источника к получателю оно подвергается нескольким преобразованиям, конечной целью которых является согласование характеристик сигнала сообщения с характеристиками канала передачи. При этом передаваемый сигнал должен однозначно отображать сведения о содержании передаваемого сообщения. Эти преобразования осуществляются путём кодирования и модуляции.

1.4.1 Кодирование и модуляция

Кодирование и модуляция – две операции преобразования дискретного сообщения в сигнал. Кодирование представляет со­бой преобразование сообщения в последовательность кодовых символов, а мо­дуляция – преобразование этих символов в сигналы, пригодные для передачи по каналу. С помощью кодирования и модуляции источник сообщений согла­суется с каналом.

Простейшим примером дискретного сообщения является текст. Любой текст состоит из конечного числа элементов: букв, цифр, знаков препинания. Их совокупность называется алфавитом источника сообщения.

При кодировании происходит процесс преобразования элементов сообще­ния в соответствующие им числа – кодовые символы. Каждому элементу сооб­щения присваивается определённая совокупность кодовых символов, которая называется кодовой комбинацией. Совокупность кодовых комбинаций, отобра­жающих дискретные сообщения, образует код. Правило кодирования может быть выражено кодовой таблицей, в которой приводятся алфавит кодируемых сообщений и соответствующие им кодовые комбинации. Множество возмож­ных кодовых символов называется кодовым алфавитом, а их количество т – основанием кода. В общем случае при основании кода т правила кодирования К элементов сообщения сводятся к правилам записи К различных чисел в т-ичной системе счисления. Число разрядов n, образующих кодовую комбина­цию, называется разрядностью кода или длиной кодовой комбинации. В зависи­мости от системы счисления, используемой при кодировании, различают двоичныe и т-ичные (недвоичные) коды.

Основание кода т, длина кодовой комбинации n, а также расстояние между кодовыми комбинациями d_ij и вес кодовой комбинации w являются основными параметрами кодов.

Расстояние d_ij характеризует различие между двумя кодовыми комбинациями и определяется по Хеммингу числом несовпадающих в них разрядов, т.е. числом единиц в сумме двух комбинаций по модулю 2. Вес w кодовой комбинации определяется числом её ненулевых элементов. Коды, у которых все комбинации имеют одинаковую длину, называют равномерными. Для равномерного кода число возможных комбинаций равно тⁿ. Применение равномерных кодов не требует передачи разделительных символов между кодовыми комбинациями.

У неравномерных кодов кодовые комбинации отличаются друг от друга как взаимным расположением символов, так и их количеством. Поэтому различные комбинации имеют различную длительность. Такие коды требуют либо специальных разделительных знаков, указывающих конец одной и начало другой кодовой комбинации, либо должны строиться так, чтобы никакая кодовая комбинация не являлась началом другой. Коды, удовлетворяющие этому условию, называются неприводимыми или префиксными. Равномерный код также является неприводимым.

По признаку помехозащищённости коды делят на примитивные (первичные) и корректирующие. Простыми или кодами без избыточности (примитивными) называются коды, у которых для передачи информации ис­пользуются все возможные кодовые комбинации. В простых равномерных кодах превращение одного символа комбинации в другой, например 1 в 0 или 0 в 1, приводит к появлению новой разрешённой комбинации, т.е. к ошибке. В корректирующих кодах для передачи сообщения используются не все кодовые ком­бинации, а лишь некоторая их часть (разрешённые кодовые комбинации). Этим создаётся возможность обнаружения и исправления ошибки при непра­вильном воспроизведении некоторого числа символов. Корректирующие свойства кодов достигаются введением в кодовые комбинации дополнительных (избыточных) символов.

Декодирование состоит в восстановлении сообщения по принимаемым ко­довым символам.

Устройства, осуществляющие кодирование и декодирование, называют соответственно кодером и декодером.

На рис. 1.4.1 изображена структурная схема системы передачи дискретных сообщений, а на рис. 1.4.2 поясняется процесс преобразования дискретного сообщения в сигнал.

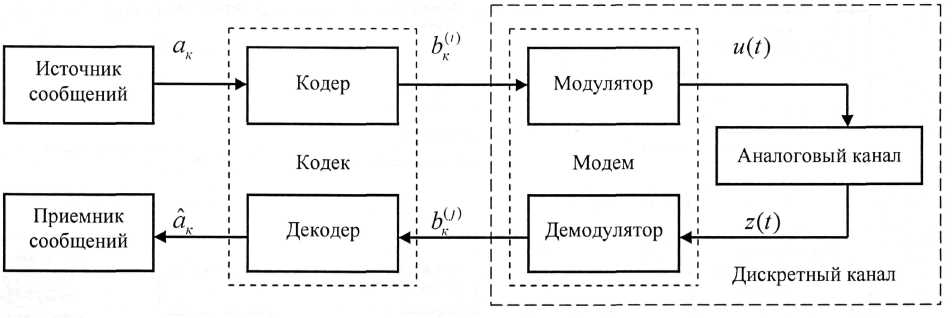
Рисунок 1.4.1 – Структурная схема системы передачи дискретных сообщений

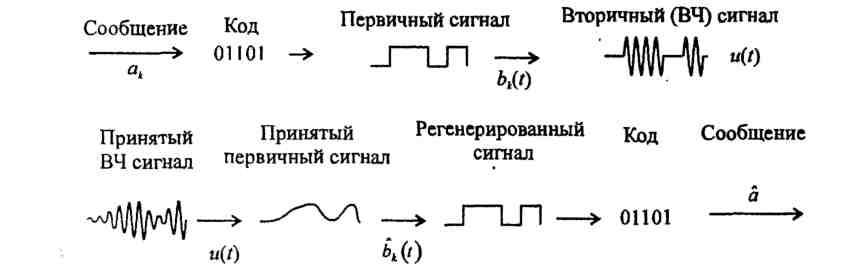
Рисунок 1.4.2 – Процесс преобразования дискретного сообщения в сигнал и сигнала в дискретное сообщение

На них приняты следующие обозначения: а_к – передаваемое сообщение; b_k(t) – кодированное сообщение (или первичный цифровой сигнал); (k – номер последовательно передаваемого символа, i – номер по­зиции кода, i = ) – его ком­поненты; u(t) – сигнал, поступающий в линию связи; z(t) – принятый сигнал; (её компоненты ) – восстановленная последовательность кодовых сим­волов и – декодированное (восстановленное) сообщение.

Вследствие воздействия помех принятый сигнал отличается от пе­реданного, а восстановленное сообщение может не совпадать с исходным.

В современных системах передачи дискретных сообщений принято разли­чать две группы относительно самостоятельных устройств: кодеки и модемы. Кодеком называются устройства, преобразующие сообщение в код (кодер) и код в сообщение (декодер), а модемом – устройства, преобразующие код в сигнал (модулятор) и сигнал в код (демодулятор). Канальные устройства (полосовые усилители передатчика и приёмника, корректоры и т.п.) вместе с линией связи образуют непрерывный канал, а последний вместе с модемом – дискретный канал.

Эф­фективность введения в тракт кодирующих и декодирующих устройств, цель которых состо­ит в согласовании свойств источника сообщений со свой­ствами канала связи, обосновал в своих основных теоремах Шеннон. Исходя из этих теорем, кодек решает две задачи.

Первая задача состоит в кодировании источника сообщений (кодер источника), при котором путем уст­ранения избыточности существенно снижается среднее число символов, требующихся на букву сообщения. Статистические свойства источника сообщения и помех в канале связи при этом не принимаются во внимание. При отсутствии помех это непосредственно дает выигрыш во времени передачи или в объеме запоминающего устрой­ства, т. е. повышает эффективность системы. Поэтому такое кодирование получило название эффективного или оптимального. При наличии помех в канале оно позволяет преоб­разовать входную информацию в последовательность символов, наилучшим образом (в смысле максимально­го сжатия) подготовленную для дальнейшего преобра­зования.

С помощью второго кодирующего устройства (кодер ка­нала) обеспечивается заданная достоверность при передаче или хранении информации путем дополнитель­ного внесения избы­точности с учётом интенсивности и статистических за­кономерно­стей помехи в канале связи. Такое кодирова­ние получило назва­ние помехоустойчивого.

Выбор кодирующих и декодирующих устройств зависит от статистических свойств источника сообщений, а также уровня и характера помех в канале связи. При малой избыточности источника со­общений и отсутствии помех в канале связи введение как кодера источника, так и кодера канала нецелесооб­разно.

При высокой избыточности источника и отсутствии помех целесообразно введение кодера источника. При малой избыточность источника и больших поме­хах целесообразно введение кодера канала. При большой избыточности и высоком уровне помех целесо­образно введение обоих дополнительных кодирую­щих (и декоди­рующих) устройств.

При передаче непрерывного сообщения а (рис. 1.4.2) его сна­чала преобразу­ют в непрерывный первичный электрический сиг­нал b(t), а затем, как правило, с помощью модулятора формируют канальный (линейный) сигнал u(t), который посыла­ют в линию связи. Принятое колебание z(t) подвергается обратным преобразованиям, в результате которых выделяется первичный сигнал . По нему за­тем восстанавливается с той или иной точностью сообщение .

Общий принцип модуляции состоит в изменении одного или нескольких параметров несущего колебания (переносчика) f(t, α, β, ...) в соответствии с пе­редаваемым сообщением. Для гар­монического переносчика возможно образова­ние трёх видов модуляции: амплитудной (АМ), частотной (ЧМ) и фазовой (ФМ). Для импульсных периодических переносчиков при заданной форме импульсов v(t) возможно образование четырёх основных видов импульсной модуляции: амплитудно-импульсной (АИМ), широтно-импульсной (ШИМ), время - (ВИМ) или фазоимпульсной (ФИМ) и частотно-импульс­ной (ЧИМ). Применение радиоимпульсов позволяет получить ещё два вида модуляции: по частоте и по фазе высокочастотного заполнения.

На рисунке 1.4.3 приведены формы сигнала при двоичном коде для различных видов дискретной или цифровой модуляции (манипуляции).

Рисунок 1.4.3 – Формы сигналов при двоичном коде для

некоторых видов дискретной модуляции

Длительность посылки первичного сигнала b_ц(t) при дискретной передаче определяет скорость передачи посылок (техническую скорость или скорость мо­дуляции). Эта скорость ν выражается числом посылок, передаваемых за едини­цу времени. Измеряется техническая скорость в Бодах. Один Бод – это ско­рость, при которой за 1 с передаётся одна посылка. Если длительность посыл­ки Т выражена в секундах, то скорость модуляции ν = 1/Т Бод. Ширина спектра первичного сиг­нала, ограниченная третьей гармоникой, равна F_c = l,5ν Гц.

1.4.2 Демодуляция и декодирование

Переданное сообщение в приёмнике обычно восстанавливается в следующей последовательности. В системах передачи непре­рывных сообщений в результате демодуляции восстанавливается первичный сигнал, отображающий переданное сообщение. Этот сигнал затем поступает на воспроизводящее или записывающее устройство. В системах передачи дискретных сообщений обычно в результате демодуляции последовательность элементов сигнала превращается в последовательность кодовых символов. За­тем по ним восстанавливаются сообщения, выдаваемые получателю. Последнее преобразование называется декодированием.

В результате различных искажений и воздействия помех пришедший сигнал может существенно отличаться от переданного. Поэтому в процессе приёма такого сигнала выдвигается ряд предположений (гипотез) о том, какое сообщение передавалось. Задачей приёмного устройства является принятие решения о том, какое из возможных сообщений действительно передавалось источником. Для этого принятый сигнал подвергается анализу с учётом всех сведений об источ­нике (например, о вероятностях, с которыми источник посылает то или иное сообщение), о применяемом коде и методе модуляции, а также о свойствах ка­нала. Процесс преобразований, которым подвергаются при этом сигналы, называют обработкой сигнала. В результате анализа определяются условные (апостериорные) вероятности возможных гипотез и на основании этих вероят­ностей принимается решение, которое и поступает к получателю. Та часть приём­ного устройства, которая осуществляет анализ приходящего сигнала и прини­мает решение о переданном сообщении, называется решающей схемой.

В системах передачи непрерывных сообщений при аналоговой модуляции решающая схема определяет по пришедшему искажённому канальному (вторичному) сигналу наиболее вероятный переданный первичный сигнал и восстанавливает его. Здесь решающей схемой является демодулятор. В систе­мах передачи дискретных сообщений решающая схема чаще всего состоит из двух частей: первой решающей схемы – демодулятора и второй решающей схемы – декодера. Такой метод приёма называется поэлементным. В этом случае сначала анализируются отдельные элементы сигнала, соответст­вующие кодовым символам, а затем восстановленная кодовая комбинация де­кодируется, т.е. преобразуется в элемент (букву) сообщения.

Иногда при передаче дискретных сообщений операции демодуляции и декодирования выполняет одно устройство, которое приходящую последователь­ность элементов сигнала преобразует сразу в последовательность символов (букв) сообщения. Такой метод приёма называют совместной демодуляцией-декодированием или приёмом в целом. В этом случае анализируется целиком отрезок сигнала, соответствующий кодовой комбинации, и на основании того или ино­го критерия восстанавливается переданный элемент сообщения (буква).

Отыскание правил оптимальной обработки сигнала, при ко­торой решение о переданном сообщении оказывается наиболее достоверным, является одной из задач статистической тео­рии связи. Эти правила зависят от свойств канала и методов передачи (кодирования и модуляции).

Современная статистическая теория связи позволяет отыскать наилучший алгоритм обработки входного сигнала z(t) (правило принятия решения), обеспечивающий максимальное ка­чество оценки b_i. Такая задача была впервые поставлена и решена (для гауссовского неискажающего канала с БГШ) В.А. Котельниковым. В этой постановке качество оценивалось вероятностью правильного приёма символа. Максимум этой веро­ятности при заданном виде модуляции В.А. Котельников назвал потенциаль­ной помехоустойчивостью, а демодулятор, обеспечивающий этот максимум, – идеальным приёмником. Из этого определения следует, что ни в одном реаль­ном демодуляторе средняя вероятность правильного приёма символа не может быть больше, чем в идеальном.

Лекция 1.5 Каналы связи. Помехи и искажения

1.5.1 Классификация каналов связи

В существующей научно-технической и учебной литературе, посвящённой различным системам связи, отсутствует единое конкретное поня­тие «канал связи». Обычно под каналом связи понимают часть сис­темы связи, характеристики которой в процессе её исследования (анализа или синтеза) можно принять известными и неизменными, или же наоборот, часть системы связи, подвергающуюся исследованиям. Так, например, при исследовании условий прохождения радиосиг­нала между сотовым телефоном и базовой станцией (радиоканала) под каналом связи понимается пространство между антеннами со­тового телефона и базовой станции, при синтезе оптимального при­ёмника (демодулятора) – совокупность технических средств от вы­хода модулятора передающего устройства до входа демодулятора приёмного устройства и среды распространения сигнала.

Часть системы связи, расположенная до входа канала, явля­ется для него источником сигнала, а часть системы, расположенная после выхода канала – его получателем.

Не смотря на столь неконкретное определение, каналы связи имеют определённые общие признаки и могут быть классифициро­ваны по ним.

Основными признаками классификации каналов являются:

1) назначение системы (вид передаваемых сообщений): телефонные, телеграфные, факсимильные, звукового вещания, передачи данных, телевизионные, телеметрические и смешанные;

2) тип среды распространения: проводные (воздушные, кабельные, ВОЛС), волноводные, радио;

3) диапазон частот: для целей электросвязи в соответствие с Регламентом радиосвязи используются девять диапазонов частот – с четвертого (ОНЧ – СДВ) по двенадцатый (ГВЧ – децимиллиметровые) (табл. 1.2.1);

4) характер сигналов на входе и выходе системы:

- непрерывные (аналоговые) каналы – сигналы на входе и выходе непрерывные;

- дискретные (по уровню) – сигналы на входе и выходе дискретные;

- дискретно-непрерывные или непрерывно-дискретные (полунепрерывные) – сигнал на входе дискретный, на выходе непрерывный или наоборот.

Всякий дискретный или полунепрерывный канал содержит внутри себя не­прерывный канал. Дискретность и непрерывность канала не связана с характером передаваемых сообщений: можно передавать дискрет­ные сообщения по непрерывному каналу и непрерывные сообщения по дискретному.

Общими признаками непрерывных каналов являются:

а) большинство каналов можно считать линейными. В таких каналах вы­ходной сигнал является суммой откликов отдельных входных сигналов и помех (применим принцип суперпозиции), а продукты нелинейных преобразований в канале малы по сравне­нию с выходными сигналами;

б) на выходе ка­нала даже в отсутствие полезного сигнала все­гда имеются помехи;

в) сигнал при передаче по каналу претерпевает задержку по времени и затухание по уровню;

г) в реальных каналах всегда имеют место искажения сигнала, обусловленные несовершенством характеристик канала и, нередко, из­менениями параметров канала во времени.

Различают каналы чисто временные (с сосредоточенными параметрами), в которых сигналы на входе и выходе описываются функциями одного скаляр­ного параметра (времени t), и пространственно-временные каналы (с распре­делёнными параметрами), в которых сигналы на входе и (или) выходе описы­ваются функциями более одного скалярного параметра (например, времени t и пространственных координат х, у, z). Такие сигналы называют полями.

Каналы классифицируются также по следующим признакам:

- ширина полосы частот, занимаемых каналом (канал тональной частоты, широкополосные каналы);

- скорость передачи (основной цифровой канал, групповой цифровой канал – первичный, вторичный, третичный, четвертичный);

- способ организации двухсторонней связи (двухпроводный однополосный, двухпроводный двухполосный, четырехпроводный однополосный);

- протяженность или территориальный признак (международные, междугородние, магистральные, зоновые и местные).

1.5.2 Основные параметры каналов связи

Канал связи характеризуется так же, как и сигнал, тремя ос­новными парамет­рами:

- временем T_к, в течение которого по каналу возможна пере­дача;

- динами­ческим диапазоном D_к (отношение допустимой мощности передаваемого сигнала к мощности помехи, выраженное в децибелах);

- полосой пропускания канала F_к.

Обобщённой характеристикой ка­нала является его ёмкость (объём):

(1.5.1)

Необходимым условием неискажённой передачи по каналу сигналов с объёмом является:

(1.5.2)

В простейшем случае сигнал со­гласуют с каналом по всем трём параметрам, т.е. добиваются выполнения ус­ловий:

(1.5.3)

При этих условиях объём сигнала полностью «вписывается» в объём канала.

Неравенство (1.5.2) может выполняться и тогда, когда одно или два из неравенств (1.5.3) не выполнены. Это означает, что можно производить «обмен» длительности на ширину спектра или ширину спектра на динамический диапазон и т.д.

Наряду с приведёнными выше основными параметрами канала его частотные свойства характеризуются частотным коэффициен­том передачи , а временные – импульсной характеристи­кой h_к(t,τ). Из п. 1.2.5 следует, что эти характеристики позволяют описать преобразования входных сигналов во временной или час­тотной области, осуществляемые как каналом в целом, так и его от­дельными элементами.

1.5.3 Помехи и искажения в системах связи

В процессе прохождения по линиям связи (в среде распро­странения) сигналы испытывают ослабление (затухание), подвер­гаются различного рода искажениям и воздействию помех. В связи с этим сообщения в приёмном устройстве воспроиз­водятся с некоторой ошибкой.

Все искажения подразделяются на два основных типа: линей­ные (ЛИ) и нелинейные (НИ).

ЛИ характеризуют искажения формы и спектрального состава сигнала, прошедшего через канал передачи. Различают амплитудно-час­тотные (АЧИ) и фазочастотные искажения (ФЧИ). АЧИ обуслов­лены отклонением АЧХ канала передачи от номинального значения в диапазоне частот передаваемого сигнала, а ФЧИ – от­клонением его ФЧХ φ_к(ω) от линейной.

Для оценки и нормирования ФЧХ обычно используют харак­теристику группового времени запаздывания (ГВЗ):

(1.5.4)

где , – время задержки составляющей спек­тра с частотой .

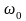Эта характеристика показывает отличие во времени прихода различных компонентов сигнала.

Условиями отсутствия ЛИ в канале являются:

- отсутствие АЧИ (или частотных) искажений:

при ; (1.5.5)

- линейная зависимость ФЧХ в полосе частот группового сиг­нала:

, k = 0, 1, 2… при . (1.5.6)

ЛИ классифицируют по следующим признакам:

1. по зависимости ЛИ от времени: постоянные и изменяю­щиеся во времени;

2. по характеру накопления ЛИ в последовательно соединен­ных цепях: ре­гулярные и случайные.

НИ в канале передачи возникают за счет нелинейности его ампли­тудной характеристики. НИ сигнала проявляются:

1. в искажении его формы;

2. в обогащении спектра выходного сигнала дополнительными составляющими по сравнению с входным сигналом.

НИ (гармонические и комбинационные) очень сильно зависят от уровня сигнала на входе канала передачи.

ЛИ и НИ, обусловленные известными характеристиками ка­нала, могут быть устранены соответствующей коррекцией.

В отличие от искажений помехи имеют случайный ха­рактер, они заранее не известны и поэтому не могут быть полностью уст­ранены.

Помехой называется любое случайное воздействие на сигнал, изменяющее значение его информационных параметров и тем са­мым ухуд­шающее верность воспроизведения передаваемых сооб­щений. Помехи отличаются по своему происхождению, физиче­ским свойствам и способу воздействия на сигнал.

В общем случае помехи подразделяются на внешние, посту­пающие на вход приёмного устройства из канала связи, и внут­ренние, возникающие в самом приёмном устройстве.

Внешние помехи возникают вследствие различных естест­венных электромагнитных процессов, происходящих в атмосфере, ионосфере и космическом пространстве (атмосферные помехи, космические шумы и т. д.). Кроме того, они создаются различного рода электроустановками (индустриальные помехи) и многочис­ленными посторонними радиостанциями.

Внутренние шумы (помехи) возникают вследствие хаотиче­ского теплового движения электронов и ионов в элементах самого приёмного устройства. Основные источники этих шумов – элек­тронные лампы, полупроводниковые приборы, сопротивления и другие элементы схемы.

Как внешние, так и внутренние помехи накладываются на сигнал и искажают его. Характерной особенностью этих видов по­мех является то, что они независимы от сигнала и имеют место даже тогда, когда сигнал на входе приёмного устройства отсутст­вует. На основании этого свойства внешние и внутренние помехи получили название аддитивных помех, а их воздействие на сигнал представляется оператором:

(1.5.7)

где 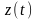– входной сигнал, – полезный сигнал, – аддитив­ная помеха.

По своим свойствам аддитивные помехи можно разбить на три группы: флюктуационные, сосредоточенные по спектру (узко­полосные или синусоидальные) и импульсные (сосредоточенные по времени).

Флюктуационная помеха в общем случае представляет со­бой хаотическое, беспорядочное изменение во времени напряжения или тока в какой-либо электрической цепи, вызванное случайным тепловым движением электронов в любом проводнике. При теле­фонной связи флюктуационная помеха проявляется в виде харак­терного шума, слышимого в телефонах. Поэтому её часто называют просто шумом. Флюктуационные помехи существуют на выходе приёмного устройства непрерывно, а их спектр практически запол­няет всю его полосу частот.

В последующих лекциях для наименования некоторых важ­нейших видов флюктуационных помех применяются такие тер­мины, как «белый шум» (БШ), «квазибелый шум» (КБШ) и «гаус­совский шум» (ГШ). Под белым шумом понимается стационарный случайный процесс, имеющий равномерный частотный спектр во всём диапазоне частот от 0 до ∞. Если спектр равномерен в ограни­ченной полосе часто и равен нулю за её пределами, то такой слу­чайный процесс называется квазибелым шумом. Гауссовским или нормальным называют шум, имеющий гауссовский (нормальный) закон распределения, при этом спектр шума может быть любым. В соответствии с этой терминологией нормальным белым шумом (НБШ) или белым гауссовским шумом (БГШ) называют стацио­нарный случайный процесс, имеющий нормальный закон распреде­ления и равномерный частотный спектр.

БШ после прохождения через любую линейную цепь превра­щается на выходе этой цепи в процесс с нормальным законом рас­пределения, что даёт основание полагать закон распределения БШ нормальным.

Флюктуационные помехи могут считаться гауссовским слу­чайным процессом (СП) с ну­левым средним и спектральной плот­ностью мощности:

,

где k = 1,38∙10^-23 Дж/град – по­стоянная Больцмана; Т – абсолютная температура источника шума; N₀ – односторонняя (на положитель­ных частотах) спек­тральная плотность шума.

Сумма большого числа любых помех от различных источни­ков вследствие условий центральной предельной теоремы теории вероятностей также имеет характер флюктуационной помехи. Мно­гие помехи при прохождении через приёмное устройство часто приобретают свойства нормальной флюктуационной помехи.

Сосредоточенная помеха получила своё название в силу того, что основная часть её мощности сосредоточена в отдельных относительно небольших участках диапазона частот, как правило, меньших полосы пропускания приёмного устройства. Обычно ос­новная часть мощности сосредоточенной помехи располагается в полосе частот, соизмеримой с величиной 1/Т, где Т – длительность элемента сигнала при передаче дискретных сообщений. Такие по­мехи имеют относительно длительный характер и представляют собой синусоидальные колебания высокой частоты, модулирован­ные по одному или нескольким параметрам (амплитуде, частоте, фазе). Сосредоточенные помехи создаются сигналами посторон­них радиостанций, а также излучениями генераторов высокой час­тоты различного назначения (промышленных, медицинских и т. п.). Изменение параметров сосредоточенной помехи в месте приёма зависит от условий формирования сигналов источников помех, от условий распространения этих сигналов и, как правило, имеет случайных характер.

Под импульсной помехой принято понимать такую регулярную или хаотическую последовательность мешающих импульсов, при которой за время длительности элементарного сигнала Т на вход приёмного устройства поступает один или небольшое число импульсов. Мешающим импульсом является любая помеха, длительность которой τ значительно меньше длительности элементарного сигнала Т. Спектр такой помехи заполняет всю полосу частот приёмного устройства, а её энергия может быть весьма значительной. К импульсным помехам относятся многие атмосферные помехи (например, грозовые разряды) и промышленные помехи (от устройств зажигания двигателей внутреннего сгорания, линий электропередач, газовые разряды).

Понятия «флюктуационная» и «импульсная помеха» являются относи­тельными. В зависимости от частоты следования импульсов одна и та же поме­ха может воздействовать как импульсная на приёмник с широкой полосой пропускания и как флюктуационная на приёмник с относительной узкой поло­сой пропускания. На практике импульсные помехи приходится рассматривать как случайный, относительно широкополосный (тем шире, чем короче им­пульсы помехи) процесс, состоящий из отдельных редких, случайно распреде­лённых во времени и по амплитуде импульсов. Вероятностные свойства таких помех с достаточной для практики полнотой описываются распределением вероятностей амплитуд импульсов и распределением временных интер­валов между этими импульсами. Для последних часто применяют модель Пу­ассона.

Распределение амплитуды импульсных помех часто описывается логарифмически нормальным законом:

,

где а, σ² – соответственно математическое ожидание (МО) и дисперсия преобразованного СП.

Для этого закона характерно наличие существенных значений в области больших амплитуд, что адекватно реальным импульсным помехам.

В диапазоне оптических частот тепловой шум оказывается очень слабым. Однако при слабых сигналах существенное значение имеет квантовый шум, вызванный дискретной природой светового излучения. Энергия оптического сигнала излу­чается и поглощается квантами, причём энергия одного такого кванта (фотона) равна Е_Ф =hf, где h = 6,624∙10^-34 Дж∙с – постоянная Планка; f – теку­щая частота. В элементарном сигнале длительностью Т с высокостабильной несу­щей частотой f (когерентное одномодовое излучение) и амплитудой U детер­минированной может быть только средняя энергия (пропорциональная U²) Е_ср = mhf (m – среднее число фотонов на интервале T). Конкретная же реали­зация элементарного сигнала имеет энергию Е = nhf, где п – случайное число регистрируемых фотонов.

Реальные системы оптической связи отличаются от идеальных:

- фазовым дрожанием цифрового сигнала(непостоянство времени передачи бита информации);

- непостоянством излучаемой оптической энергии, вызванной шумами передатчика и лазера, а также фотодетектора;

- наличием межсимвольной интерференции.

Шум лазера имеет квантовую природу. Веро­ятность появления точно п фотонов на интервале Т на передающей стороне определяется распределением Пуассона:

, n = 0, 1, 2, …, m = vT, v – интенсивность потока,

т.е. шум лазера – это квантовый шум, так как он проявляется во флуктуациях параметров сигнала, детерминированного по классическим пред­ставлениям. Этот шум не является аддитивным, так как зависит от самого по­лезного сигнала. С учётом этого в приведённой формуле следует считать, что при передаче «1» т = т₁, а при передаче «0» т = т₀. При передаче «0» (отсутствие возбуждения лазера) может наблюдаться определённый, хотя и малый уровень энергии, обусловленный тем, что вероятность непоявле­ния фотонов на этом интервале р(0) = , где т₀ – среднее число шумовых фотонов на интервале Т при отсутствии возбуждения лазера. По мере увеличе­ния средней мощности излучаемого сигнала Р_пер вклад квантового шума по сравнению с другими шумами тракта передачи падает.

Шум фотодетектора имеет природу, аналогичную шуму лазера. Если за отрезок времени Т на фотодиод падает оптическая энергия, равная в сред­нем Е_пр, то следует ожидать, что будет создано в среднем N пар носителей за­ряда, причём:

,

где – квантовая эффективность взаимодействия, показывающая среднее от­ношение числа рождаемых фотодетектором электронно-дырочных пар к числу падающих фотонов ( < 1), С – скорость света, – длина волны. Вследствие стохастической природы взаимодействия фотонов с фотодетек­тором истинное число пар носителей заряда, генерируемых каждым оптиче­ским импульсом, будет флюктуировать вокруг среднего значения N. Вероят­ность того, что число созданных пар носителей заряда на интервале Т равно k, определяется пуассоновским распределением:

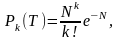k = 0, 1, 2, …

В реальных оптических линиях связи помимо кван­тового шума существуют и другие мешающие факторы (в том числе аддитив­ные помехи), что приводит к необходимости увеличения мощности оптическо­го сигнала.

Другим весьма распространённым фактором снижения верности передаваемой информации являются искажения сигналов за счёт случайного изменения состояния канала связи. Такие искажения вызывают случайную модуляцию сигнала по амплитуде, частоте или фазе и проявляются только при прохождении сигнала по реальному каналу связи. Они получили название мультипликативных помех, представляемых оператором:

(1.5.8)

где k(t) – случайный процесс, выражающий мультипликативную помеху.

Следует заметить, что мультипликативную помеху всегда можно свести к эквивалентной аддитивной. Это обстоятельство во многом упрощает исследование действия мультипликативной помехи. Действительно, если записать выражение (1.4.8) в виде:

где k₀(t) – среднее значение случайного процесса k(t), n_э(t) – эквивалентная аддитивная помеха, то получаем:

.

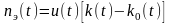После этого можно пользоваться результатами, полученными для аддитивной помехи, беря её равной n_э(t).

Одним из наиболее распространённых типов мультипликативных помех, присущим большинству радиоканалов, является эффект замираний сигнала на входе приёмного устройства, т. е. эффект непрерывных и беспорядочных флюктуаций уровня сигнала в точке приёма. Физически в канале с замираниями обычно сигнал распространяется по нескольким путям. Вследствие разности хода лучей, приходящих от передатчика к приёмнику, сигнал в приёмнике представляет сумму отдельных колебаний с различными фазами и амплитудами:

(1.5.9)

где К_i и ∆t_i – коэффициент передачи и запаздывание сигнала i-го луча, n – количество лучей.

Интерференция этих колебаний в условиях, когда разности хода лучей не остаются постоянными, и является основной причиной флюктуаций как амплитуд, так и фаз составляющих сигнала. В зависимости от характера этих флюктуаций различают общие (гладкие) и селективные, быстрые и медленные замирания. При гладких замираниях приходящий сигнал отличается от переданного случайными, но приблизительно одинаковыми для всех частотных составляющих сигнала значениями коэффициента передачи и сдвига фазы. При селективных замираниях каждой частотной составляющей сигнала соответствует свой коэффициент передачи и сдвиг фазы. Как общие, так и селективные замирания вызывают колебания уровня принимаемого сигнала со средним периодом от нескольких минут до долей секунды.

Медленные замирания имеют место, если К_i и ∆t_i характеризуются примерно одинаковыми значениями на протяжении приёма нескольких следующих друг за другом элементов сигнала. Для быстрых замираний характерно отсутствие взаимозависимости (корреляции) между значениями К_i и ∆t_i для ряда последовательно передаваемых элементов сигнала. В общем случае для оценки вида замираний важно соотношение между скоростью замираний и скоростью передачи. В этом случае замирания называют медленными, если средний период замираний τ_к (время корреляции замираний) значительно превышает длительность элемента сигнала Т (τ_к >>Т), и быстрыми, если τ_к одного порядка с Т или меньше Т.

Лекция 1.6 Сети связи

Для обмена сообщениями между многими территориально разнесёнными пользователями (абонентами) создаются сети связи. Они обеспечивают передачу и распределение сообщений по заданным ад­ресам. Распределение потоков сообщений по заданным адресам осуществляется на узлах связи с помощью коммутационных устройств. По способу распре­деления сообщений сети делятся на некоммутируемые и комму­ти­руемые. В первом случае связь между абонентами осуществляется по посто­янно закреплённым каналам по принципу «каждый с каждым». Во втором слу­чае абоненты связываются между собой не непосредст­венно, а через узлы ком­мутации. Сеть связи представляет собой со­вокупность оконечных (абонентских) устройств, каналов связи (соеди­нительных линий) и узлов коммутации и систем управления. В зави­симости от числа або­нентов и размеров обслуживаемой территории сети могут иметь раз­личную структуру: линейную, радиальную, кольцевую, радиально-уз­ловую и т.п. Задача оптимального построения сетей связи является од­ной из важней­ших задач теории и техники связи. Решается эта задача с помощью теории графов и теории массового обслуживания.

Основой электросвязи Российской Федерации является Единая сеть электросвязи (ЕСЭ) РФ, обеспечивающая предоставление услуг электросвязи пользователям на территории России. ЕСЭ РФ – сеть электросвязи, состоящая из расположенных на территории РФ сетей связи следующих категорий: сетей общего пользования (ОП), выделенных сетей, технологических сетей, сетей связи специального назначения и других сетей передачи информации при помощи электромагнитных систем.

Сети электросвязи классифицируются по следующим основным признакам.

1. По типу передаваемых сообщений: телефонные, телеграфные, передачи данных, факсимильные, звукового и телевизионного вещания, цифровые сети интегрального обслуживания и т.д.

2. По категории пользователей: общего пользования, ведомственные (корпоративные).

3. По скорости передачи сообщений: низко-, средне- и высокоскоростные.

4. По территориальному делению: международные, междугородние, зоновые и местные (городские и сельские).

5. По размеру (степени охвата): глобальные, региональные (зональные), локальные.

6. По способу коммутации: с долговременной (кроссовой) коммутацией; с оперативной коммутацией; с коммутацией каналов (КК), сообщений (КС) и пакетов (КП); с гибридной (ГК) и адаптивной (АК) коммутацией.

7. По типу используемых каналов связи: проводные, кабельные, в т.ч. волоконно-оптические, радиосети, спутниковые.

8. По способу управления сетью: централизованного, децентрализованного, смешанного, статического, квазистатического и динамического управления.

По функциональному принципу сети ЕСЭ разделяются на транспортные сети и сети доступа.

Транспортной является часть сети связи, выполняющая функции переноса (транспортирования) потоков сообщений от их источников из одной сети доступа получателям сообщений другой сети доступа.

Сетью доступа является часть сети связи, связывающая источник (приёмник) сообщений с узлом доступа, являющимся граничным между сетью доступа и транспортной сетью.

По способам организации каналов сети ЕСЭ разделяются на первичные и вторичные.

Первичные сети (ПС) предназначены для организации и предоставления во вторичные сети типовых сетевых систем (трактов) передачи и типовых физических цепей. В состав ПС входят сетевые узлы, сетевые станции и линии (каналы) передачи.

Сетевой узел (СУ) – комплекс технических средств (КТС), обеспечивающий соединение сетевых станций первичной сети, образование и перераспределение сетевых трактов, типовых каналов передачи и типовых физических цепей, а также представление их ВС и спецпотребителям.

Сетевая станция (СС) – КТС, обеспечивающий образование и предоставление ВС типовых физических цепей, типовых каналов передачи и сетевых трактов, а также их транзит.

Система передачи (СП) – применительно к сетям связи общее определение, данное в п. 1.2.1, уточняется в следующем виде: СП – это КТС и среды распространения, обеспечивающих передачу сигнала электросвязи в определенной полосе частот или с определенной скоростью передачи между СС, СУ или между СС и СУ, а также между СС или СУ и оконечным устройством ПС.

СП обеспечивают образование линейного тракта, типовых групповых трактов и каналов передачи ПС. Системы передачи разделяют на аналоговые и цифровые, проводные (электрические и оптические) и радиорелейные.

Групповой тракт – КТС, предназначенный для организации нормализованного числа типовых каналов в полосе частот или со скоростью передачи, соответствующей данному групповому тракту.

Групповой тракт, параметры и структура которого соответствуют принятым нормам, называют типовым. Например, это первичный аналоговый тракт с полосой частот 60…108 кГц или первичный цифровой тракт со скоростью передачи 2048 Кбит/с.

Линейный тракт системы передачи – КТС, обеспечивающий передачу сигналов электросвязи в полосе частот или со скоростью, соответствующей данной системе передачи. Линейный тракт может быть радиорелейным, кабельным (оптическим или электрическим), по типу системы передачи – аналоговым или цифровым.

На основе типовых трактов, типовых каналов передачи и типовых физических цепей ПС ЕСЭ РФ с помощью узлов и станций коммутации организуются различные вторичные сети (ВС) для транспортировки, коммутации и распределения сигналов в службах электросвязи. На базе ВС организуются системы электросвязи (СЭ), представляющие собой КТС, осуществляющих электросвязь определенного вида и включающие в себя соответствующую ВС и подсистемы нумерации, сигнализации, учёта стоимости и расчётов с абонентами, технического обслуживания и управления. СЭ может включать в себя одну или несколько служб электросвязи и одну или несколько сетей электросвязи.

Служба электросвязи (СлЭ) представляет собой организационно-техническую структуру на базе сети связи (или совокупности сетей электросвязи), обеспечивающую обслуживание связью пользователей с целью удовлетворения их в определенном наборе услуг электросвязи.

В зависимости от принадлежности сети связи подразделяются на:

- общего пользования – составная часть ЕСЭ РФ, открытая для пользования всем физическим и юридическим лицам;

- ведомственные (корпоративные) – сети электросвязи министерств и иных федеральных органов исполнительной власти, промышленных объединений и предприятий, создаваемые для удовлетворения производственных и специальных нужд, в масштабе как одного, так и нескольких государств, имеющие выход на сеть связи общего пользования. Корпоративные строятся так же, как и сети связи общего пользования. Они состоят из ПС и ВС.

- наложенные – сетевая структура, которая строится параллельно существующей сети, как правило, с использованием новых методов передачи и коммутации (например, цифровых) и сопрягается с существующей сетью на различных иерархических уровнях.

Выводы по теме 1

1. Передача сообщений по каналам связи осуществляется с помощью сигналов, которые яв­ляются материальными носителями сообщений, отображающих ту или иную информацию. Характерной особенностью сообщений (сигналов) является их непредсказуемость. О лю­бом cooбщении можно говорить лишь как о возможном с некоторой вероятностью собы­тии. Процесс передачи сообще­ний всегда является вероятностным (стохастическим).

2. Сообщения и соответствующие им сигналы могут быть дискретными и непрерывными. Непрерывный канальный сигнал формируется с помощью модуляции, а дискретный – с помощью кодирования и модуляции. Кодирование определяет закон построения сигнала, а модуляция – вид сигнала, который передаётся по каналу.

3. В качестве интегральных системных характеристик линейных цепей чаще всего используют импульсную характеристику и передаточную функцию системы, связанные парой пре­образований Фурье.

4. Спектральная плотность по Фурье сигнала на выходе линейной стационарной системы определяется произведением спектральной плотности сигнала на входе и передаточной функции системы. Выходной сигнал можно найти по его спектральной плотности обрат­ным преобразованием Фурье (спектральный метод анализа). Его же можно найти свёрткой входного сигнала и импульсной характеристики системы (временной метод анализа).

5. Непрерывное сообщение (сигнал) в цифровых системах связи преобразуется в цифровой сигнал с помощью трёх операций: дискретизации по времени, квантования по уровню и кодирования.

6. Основными устройствами системы передачи дискретных сообщений являются кодек и мо­дем. Канальные устройства вместе с линией связи образуют непрерывный канал, а последний вместе с модемом – дискретный канал.

Контрольные вопросы по теме 1

1. В чем разница между понятиями информация, сообщение, сигнал?

2. Изобразите структурную схему системы передачи дискретных сообщений и объясните назначение каждого из её элементов.

3. В чем различие и единство процессов кодирования и модуляции? Какова роль этих процессов в системах связи?

4. В чем существенное отличие помех от искажений?

5. В чем проявляется единство и противоположность сигналов и помех?

6. На какие основные классы подразделяются аддитивные помехи?

7. Что понимают под квантовым шумом в оптических линиях связи?

8. Приведите примеры мультипликативных помех в радио и проводных каналах. Объясните причины их возникновения.

9. Укажите признаки классификации каналов связи.

10. Какой канал называется непрерывным, дискретным и дискретно-непрерыв­ным?

11. Как связаны между собой импульсная и передаточная характеристики линейной системы?

12. Какие физические характеристики сигнала определяют его объем?

13. Как осуществляется демодуляция и декодирование в системах передачи дискретных сообщений?

14. Поясните принцип дискретизации и кодирования непрерывных сигналов

Список литературы по теме 1

1. Теория электрической связи: Учебник для вузов /Зюко А.Г., Кловский Д.Д., Коржик В.И., Назаров М.В. - М.: Радио и связь, 1999. - 432 с.

2. Зюко А.Г., Кловский Д.Д., Назаров М.В., Финк Л.М. Теория передачи сигналов. - М.: Радио и связь, 1986.

3. Теоретические основы информационной техники: Учеб. пособие для вузов/ Ф.Е. Темников, В.А. Афонин, В.И. Дмитриев. – 2-е изд., перераб. и доп. – М.: Энергия, 1979. – 512 с.

4. Финк Л.М. Теория передачи дискретных сообщений. – М.: Сов.радио, 1970, - 728 с.

5. Харкевич А.А. Борьба с помехами. – М.: Наука. 1965, - 276 с.

6. Скляр, Бернард. Цифровая связь. Теоретические основы и практическое применение. Пер с англ. – М.: Издательский дом «Вильямс», 2004. – 1104 с.