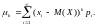- •Функция распределения случайной величины и ее свойства.
- •28.Неравенство Маркова и Чебышева
- •29. Закон больших чисел « в форме» теоремы Чебышева.
- •Теорема Бернулли.
- •18.Математическое ожидание дискретной и непрерывной случайной величины и их свойства.
- •Аксиоматическое определение вероятности. Геометрическое определение вероятности.
- •15. Плотность распределения вероятностей и ее свойства.
- •14. Дискретные случайные величины.
- •16. Функция одной случайной величины.
- •17. Случайный вектор. Система случайных величин.
Аксиоматическое определение вероятности. Геометрическое определение вероятности.
Геометрической вероятностью события А называется отношение меры области, благоприятствующей появлению события А, к мере всей области.
Аксиоматическое определение вероятности :Пусть Ω - множество всех возможных исходов некоторого опыта (эксперимента). Согласно аксиоматическому определению вероятности, каждому события А (А подмножество множества Ω) ставится в соответствии некоторое числу р(А), называемое вероятностью события А, причем так, что выполняются следующие три условия (аксиомы вероятностей):
Аксиома неотрицательности: Вероятность любого события A € S неотрицательна, т.е.:Р(А)≥0
Аксиома нормативности: Вероятность достоверного события равна единице, т.е.: P(Ω)=1/
Аксиома аддитивности: Вероятность суммы несовместимых событий равна сумме вероятностей этих событий т.е. если Ai*Aj=Ø, i≠j, то
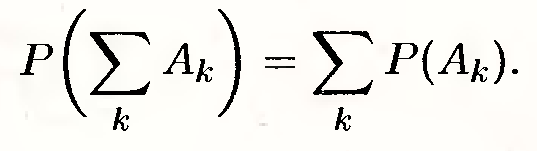
Из этих трех аксиом, вытекают свойства вероятности:
р(Ø)=0, т.е. вероятность невозможного события равна нулю.
р(А)+р(Ā)=1
0≤р(А)≤1 для любого события А
р(А)≤р(В), если А подмножество В
15. Плотность распределения вероятностей и ее свойства.
Плотностью
распределения вероятностей
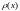 непрерывной случайной величины
Х
непрерывной случайной величины
Х
называют предел, если он существует, отношения вероятности попадания случайной величины
Х на отрезок
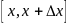 ,
примыкающей к точке
,
примыкающей к точке
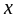 ,
к длине этого отрезка, когда
,
к длине этого отрезка, когда
последний стремится к 0, т.е.
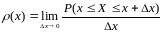 .
.
Свойства плотности распределения вероятностей:
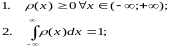
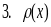 -
непрерывная
или кусочно непрерывна функция;
-
непрерывная
или кусочно непрерывна функция;
14. Дискретные случайные величины.
Случайная величина
, обозначаемая
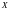 , называется дискретной,
если она принимает
, называется дискретной,
если она принимает
конечное либо
счетное множество значений, т.е.
множество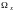 -конечное,
либо счетное.
-конечное,
либо счетное.
Законом распределения дискретной случайной величины называется совокупность пар
чисел
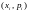 ,
где
,
где
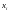 -
возможные значения случайной величины,
а
-
возможные значения случайной величины,
а
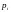 -
вероятности, с которыми она принимает
эти значения, причем
-
вероятности, с которыми она принимает
эти значения, причем
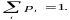
Зная закон распределения случайной величины, можно вычислить функцию распределения:
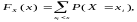
где суммирование
распространяется на все значения индекса
 ,
для которых
,
для которых
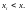
Математическим
ожиданием
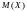 дискретной случайной величины
называется сумма произведений всех ее
возможных значений и соответствующих
им вероятностей:
дискретной случайной величины
называется сумма произведений всех ее
возможных значений и соответствующих
им вероятностей:
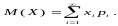
Модой дискретной
случайной величины, обозначаемой
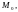 называется ее наиболее вероятное
значение.
называется ее наиболее вероятное
значение.
Медианой
случайной
величины
называется такое ее значение
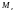 , для которого одинаково вероятно,
окажется ли случайная величина меньше
или больше
,
т.е.
, для которого одинаково вероятно,
окажется ли случайная величина меньше
или больше
,
т.е.
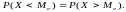
Дисперсией случайной величины называется математическое ожидание квадрата ее отклонения:
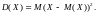
Дисперсия дискретной случайной величины вычисляется по формуле:
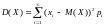 или
или
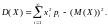
Средним
квадратическим отклонением (стандартом)
случайной величины
называется арифметический корень из
дисперсии, т.е.
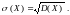
Начальным моментом
порядка
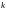 случайной величины
называется математическое ожидание
-й
степени этой случайной величины, т.е.
случайной величины
называется математическое ожидание
-й
степени этой случайной величины, т.е.
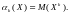
Для дискретной
случайной величины
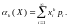
Центральным
моментом порядка
случайной величины
называется математическое ожидание
-й
степени отклонения
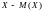 ,
т.е.
,
т.е.
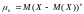 .
.
Для дискретной
случайной величины