3.2. Фазові портрети лінійної системи другого порядку. Типи особливих точок

Нехай вільний рух системи описується таким лінійним диференціальним рівнянням другого порядку

, (7)

тоді характеристичне рівняння матиме вигляд

і розв’язок диференціального рівняння запишеться у вигляді

,

де - корені характеристичного рівняння;С₁, С₂ – константи, які залежать від початкових умов. Розглянемо фазові траєкторії та портрети системи при різних коренях характеристичного рівняння.

1. Припустимо, що в рівнянні (7) і λ₁ і λ₂ - уявні корені

.

Відомо, що при наявності уявних коренів в системі виникають незникаючі коливання, амплітуда і частота яких залежить від початкових умов (див рисунок)

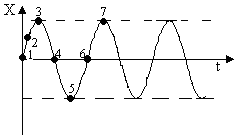
Зведемо рівняння (7) до системи двох рівнянь

,

звідки вилучаючи , одержимо диференціальне рівняння фазової траєкторії

,

розв’язок якого

є рівнянням еліпса, осі якого залежать від константи С, тобто від початкових умов. Графічно фазовий портрет системи показаний на рисунку.

Особливою точкою на фазовій площині є початок координат і ця точка називається центром.

2. Припустимо, що корені λ₁ і λ₂ є комплексні з від'ємною дійсною частиною

.

Це означає, що система є стійкою, а перехідний процес буде коливним і заникаючим. Фазова траєкторія сходиться до початку координат

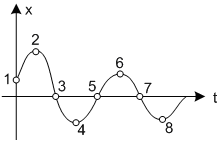
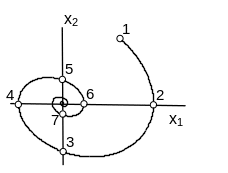
Особлива точка в такій системі знаходиться в початку координат, є точкою рівноваги і називається стійким фокусом.

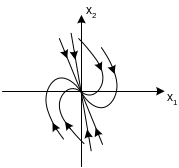
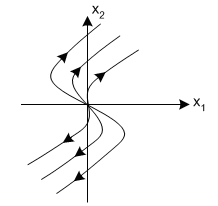
3. Припустимо, що λ₁ і λ₂ комплексні корені з додатними дійсними частинами. Система є нестійка, перехідний процес в такій системі є коливним і амплітуда коливань з часом зростає. Фазова траєкторія має вигляд спіралі, що розкручується і віддаляється від початку координат.

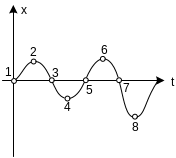
Особлива точка – нестійкий фокус.

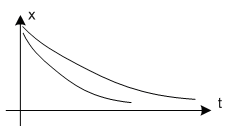
4. Припустимо корені характеристичного рівняння є дійсні і додатні. Така система є нестійкою і в ній виникатимуть розбіжні аперіодичні процеси

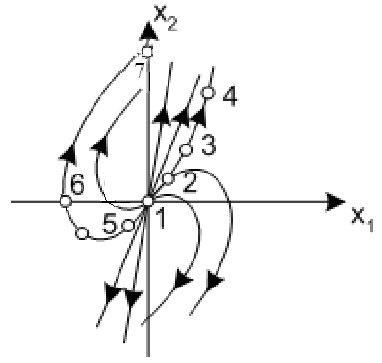
Особлива точка такої системи називається нестійким вузлом.

5. Корені є дійсні і від'ємні. Система є стійкою, а перехідні процеси в ній аперіодичні.

Особлива точка – стійкий вузол.

6. Корені дійсні і різні за знаком.

Особлива точка – сідло.

7. Корені дійсні однакові і від'ємні. 8. Корені дійсні рівні і додатні

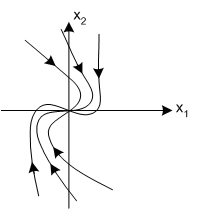
Особлива точка - Особлива точка -

вироджений нестійкий вузол. вироджений стійкий вузол.

Такі портрети властиві також і нелінійним системам, але з несуттєвими нелінійностями. Якщо система лінеаризується в околі особливої точки, то тип особливої точки однозначно визначається коренями характеристичного рівняння лінеаризованої системи:

стійкий вузол – корені дійсні від`ємні;

нестійкий вузол – корені дійсні додатні;

стійкий фокус – корені комплексні з від`ємною дійсною частиною;

нестійкий фокус – корені комплексні з додатною дійсною частиною;

центр – корені уявні;

сідло – корені дійсні різного знаку.

3.3. Побудова фазових траєкторій системи автоматичного регулювання

В найпростішому випадку нелінійну систему можна розглядати як таку, що складається з нелінійної та лінійної частин. Структурна схема такої системи показана на рис. 1.

Рис. 1. Структурна схема САР з одним нелінійним елементом.

Наявність в системі суттєво нелінійного елементу зумовлює якісно інший фазовий портрет системи, ніж в лінійній системі. В загальному випадку задача знаходження диференціального рівняння фазової траєкторії нелінійної системи та його розв’язок є складною задачею. Ситуація дещо спрощується якщо нелінійний елемент можна представити кусково лінійним (тобто лінійним в певних інтервалах зміни вхідної величини), тоді в межах кожного такого інтервалу фазові траєкторії відповідають фазовим траєкторіям лінійної системи. При переході з одного інтервалу на інший змінюється рівняння фазових траєкторій. Сукупність фазових траєкторій на кожному інтервалі складає загальну фазову траєкторію, яка будується за допомогою методу допасовування. Згідно з цим методом побудова фазової траєкторії здійснюється в три етапи:

а) модель нелінійної системи записують у вигляді набору лінійних моделей, що відповідають лінійним ділянкам нелінійного елементу;

б) фазовий простір (площину) розбивають на області, в яких система описується лінійними рівняннями;

в) послідовно отримують рівняння фазових траєкторій на кожній ділянці та об’єднують (допасовують) їх в єдину фазову траєкторію нелінійної системи.