3. Дослідження нелінійних систем методом фазового простору

3.1. Поняття фазового простору, фазового портрету. Рівняння фазових траєкторій

В загальному вигляді вільний рух системи описується таким рівнянням

, (1)

де - вихідна величина; - похідні відповідно першого та n-ого порядків. Якщо ввести допоміжні змінні, а саме

, (2)

то рівняння (1) можна записати у вигляді системи п диференціальних рівнянь першого порядку, яка в нормальній формі матиме вигляді.

(3)

Стан динамічної системи n-го порядку у фіксований момент часу однозначно визначається значеннями n незалежних змінних в цей момент часу . Ці значення змінних будемо розглядати як координати точки в n вимірному просторі, а саму точку зображуючою. Цей n вимірний простір називається простором станів або фазовим простором, а змінні - фазовими координатами. В часі значення змінних змінюються і зображуюча точка у фазовому просторі рухається по кривій, яка називається фазовою траєкторією.

Сукупність фазових траєкторій, що відповідають різним початковим умовам системи називають фазовим портретом. Фазовий портрет охоплює всі можливі динамічні режими в системі.

Метод фазового простору найбільш зручний для дослідження систем, що описуються диференціальним рівнянням другого порядку. Так, застосовуючи прийняті в (2) нові змінні , диференціальне рівняння другого порядку в загальному вигляді можна представити у вигляді системи двох диференціальних рівнянь першого порядку

(4)

Тоді фазова траєкторія такої системи буде розміщена у фазовій площині з координатами . Із системи (4) вилучимо час t, для цього поділимо друге рівняння системи (4) на перше:

(5)

в результаті чого одержимо диференціальне рівняння фазової траєкторії. Розв'язком цього диференціального рівняння є рівняння фазової траєкторії

,

де - початкова точка фазової траєкторії на фазовій площині.

З рівняння (5) бачимо такі особливості фазової траєкторії (див. рисунок):

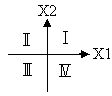
а) зображуюча точка у верхній півплощині декартової системи координат (квадранти І і ІІ), де похідна додатна, рухається зліва направо, тобто в напрямі зростання , у нижній півплощині (квадранти ІІІ і IV), де похідна від’ємна, – справа наліво;

б) у точках перетину фазової траєкторії з віссю абсцис , відповідно значення тангенсу кута нахилу дотичної згідно рівняння (5) прямує до і дотична до фазової траєкторії в цих точках перпендикулярна до цієї осі;

в) фазові траєкторії не перетинаються між собою, за винятком особливих точок та особливих траєкторій.

Таким чином, рівняння (5) однозначно визначає дотичну до фазової траєкторії в усіх її точках за винятком тих, де одночасно виконується умова

. (6)

В цих точках є невизначеність фазової траєкторії, і отже з цих точок може виходити безліч фазових траєкторій. Такі точки в фазовій площині називають особливими, в них похідні фазових координат дорівнюють нулю, тому особливі точки характеризують стан рівноваги системи. Такі точки можуть знаходитися лише на осі абсцис. Розглянемо для прикладу особливі точки і фазові портрети динамічної системи, що описується лінійним диференціальним рівнянням другого порядку.