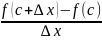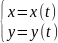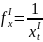Вопрос 29

Теорема Коши.

Пусть даны две функции С, непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b)

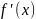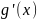- производные и не обращаются в ноль одновременно на интервале (a,b)

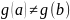- тогда

, где C (a,b)

Доказательство

Для доказательства введём функцию

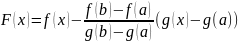
Для неё выполнены условия теоремы Ролля “(Теорема Ролля :Если функция непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.)” : на концах отрезка её значения равны f(a). Воспользовавшись упомянутой теоремой, получим, что существует точка c, в которой производная функции F равна нулю, а 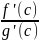равна как раз необходимому числу.

Вопрос 28

Теорема Лагранжа.

Если f(x) непрерывна на [a;b] и дифференцируема на [a;b], то существует точка c, принадлежащая отрезку [a;b], такая что справедливо равенство

F(b)-f(a)=(b-a)*f `(c)

Доказательство:

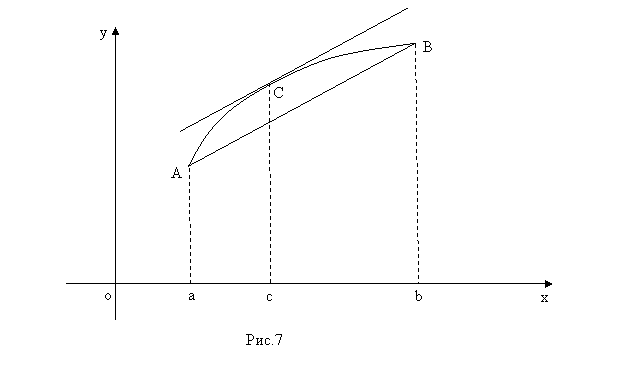
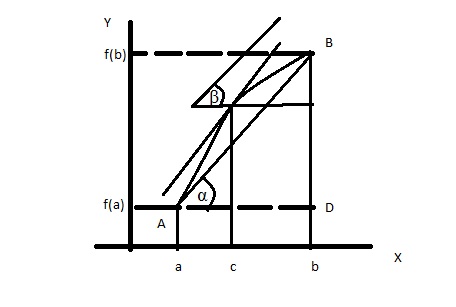
Соединим AB

Начинаем двигать AB (До касательной параллельной AB)

Касательная параллельна AB => tgα=tgβ (α=β)

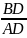= f `(c) BD = f(b)-f(a) AD = b-a

Следствие.

Если f(x) имеет f `(x) на [a;b], то внутри промежутка найдется точка c, в которой будет выполнятся равенство (Формула конечного приращения):

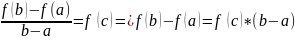
Вопрос 27

Теорема Рὁлля.

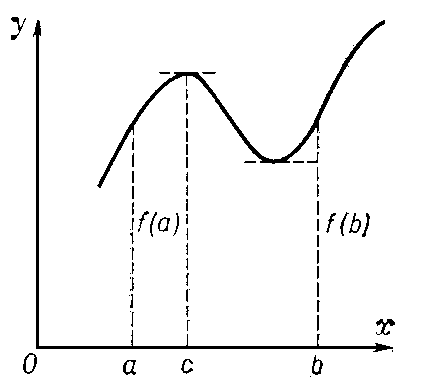
Если функция f (х) непрерывна на отрезке а ≤ х ≤ b, имеет внутри его определённую производную, а на концах принимает равные значения f (a) = f (b), то её производная f '(x) по меньшей мере один раз обратится в нуль в интервале (a, b),

        т. е. существует такое с (где a < с < b), что f’(с) = 0. Как следствие получается, что между двумя последовательными корнями функции имеется хотя бы один корень её производной.

. Функция f(x) постоянна на интервале [а, b]; тогда f ' (с) = 0 для любого с (a < с < b), т.е. утверждение теоремы Ролля выполняется автоматически.

Вопрос 26

Т. Ферма

f(x) принимает наименьшее или наибольшее значение во внутр. Тчк. «С» промежутка «Х»

Э f’(c )=>f’(c )=0

m₀<=f’(x)<=M₀

Если сущ. Производная зн. Сущ. Касательная f’(x₀)=tgL=k

1. 

Док-ть теор. Если в тчк. «С» наименьшее знач.

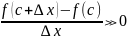
По треор. О пред. Переходе в нерав.

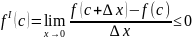
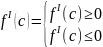
Вопрос 25

Функция заданная параметрически

Пусть зависимость между аргументом Х и функцией У задана параметрически в виде двух уравнений

1. 

где t – вспомогательная переменная, называемая параметром. Найдём производную 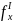, считая, что функции (1) имеют производные и что функция x = x(t) имеет обратную t = 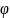(x). По правилу дифференцирования обратной функции

2. 

Функцию y = f(x), определяемую параметрическими уравнениями (1), можно рассматривать как сложную функцию y = y(t), где t= (x).

По правилу дифференцирования сложной функции имеем: .

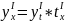С учётом равенства (2) получаем

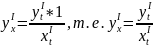
Полученная формула позволяет находить производную 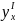от функции заданной параметрически, не находя непосредственной зависимости У от Х.

Пример:

Пусть 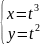Найти

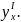
Решение: Имеем 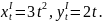Следовательно, , т.е. .

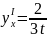В этом можно убедиться, найдя непосредственно зависимость 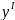от Х

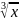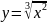Действительно, t = . Тогда . Отсюда 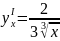, т.е. .
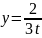