
Билет 38
Формула Тейлора для ex и её применение в приближенных вычислениях.
Пусть f(x) = ex. Тогда, как мы знаем, f(k)(x) = ex , а потому f(k)(0) = 1, а f(k)(с) = ес.
Подставить всё
это в
 или
или
 (0;x).
(0;x).
Получим формулу Тейлора для показательной функции:

Или в более подробной записи:

Отсюда следует приближённое равенство:

Позволяющее находить значение экспоненты.
Вопрос 37
Формула Тейлора для многочленов.Пусть задана функция f(x) и в некоторой точке “а” нам известны значения её и её первых n производных: f(a), f I(a), f II(a), … , f(n)(a). Мы хотим построить такой многочлен Tn (х) степени n, который в некоторой окрестности точки «а» как можно меньше отличался бы от нашей функции. Для этого мы потребуем, чтобы в точке «а» значения многочлена и его производных совпадали, соответственно, со значениями функции и ее производных.
Итак, построим многочлен Tn (х), удовлетворяющих условиям:
Tn (а) = f(a), TnI(a) = f I(a), TnII(a) = f II(a), … , Tnn(a) = f n(a).
Будем искать Tn(х) в виде
Tn(х)=c0+c1(x-a)+c2(х-a)2+...+Аn(х-a)n
Ясно, что
T'n(х)=c1+2c2(х-a)+3c3(x-a)2+...+ncn(x-a)n-1,
Tn''(х)=2c2+2•3c3(х-a)+...+n(n-1)cn(х-a)n-2,
…………………………………………………..
Tn(n)(х) = n!cn
Подставив в многочлен и его производные x=a, получим
с0 = f(a), с1 = f I(a), 2с2 = f II(a), 3!с3 = f III(a), … , n!сn = f (n)(a).
Отсюда
с0
= f(a), с1
=
f
I(a),
 ,
,
 ,
… ,
,
… ,

Таким образом
Tn
(х)
= f(a) + f I
(a)(x-a)
+
 *(x-a)2
+ ….. +
*(x-a)2
+ ….. +
 *(x-a)n
*(x-a)n
Или,
в более короткой записать,
 Здесь,
как это принято, считается, что f(0)
= f(a)
и 0! = 1.
Здесь,
как это принято, считается, что f(0)
= f(a)
и 0! = 1.
Формула Тейлора для функции
Рассмотрим подробнее величину Rn+1(x).
 Как
видно на рисунке в точке х = а значение
многочлена в точности совпадает со
значением функции. Однако, при удалении
от точки х = а расхождение значений
увеличивается.
Как
видно на рисунке в точке х = а значение
многочлена в точности совпадает со
значением функции. Однако, при удалении
от точки х = а расхождение значений
увеличивается.
Иногда используется другая запись для Rn+1(x). Т.к. точка ε ∈ (a,x), то найдется такое число θ из интервала 0 < θ < 1, что ε = a + θ(x - a).
Тогда можно записать:
 *(x-a)n+1
*(x-a)n+1
Тогда, если принять a = x0, x - a = Δx, x = x0 + Δx, формулу Тейлора можно записать в виде:

где 0 < θ < 1
Если принять n=0, получим: f(x0 + Δx) - f(x0) = f'(x0 + θΔx)Δx - это выражение называется формулой Лагранжа.
Формула Тейлора имеет огромное значение для различных математических преобразований. С ее помощью можно находить значения различных функций, интегрировать, решать дифференциальные уравнения и т.д.
Билет 7
Теорема. Если элементы сходящейся последовательности {xn}, начиная с некоторого номера, удовлетворяют неравенству xn ≥ b (xn ≤ b), то и предел a этой последовательности удовлетворяет неравенству a ≥ b (a ≤ b).
Доказательство. Пусть все элементы xn, по крайней мере начиная с некоторого номера, удовлетворяют неравенству xn ≥ b. Требуется доказать неравенство a ≥ b. Предположим, что a < b. Поскольку a - предел последовательности {xn}, то для положительного ε = b - a можно указать номер N такой, что при n ≥ N выполняется неравенство |xn - a| < b - a. Это неравенство эквивалентно следующим двум неравенствам: -(b - a) < xn - a < b - a. Используя правое из этих неравенств, получим xn < b, а это противоречит условию теоремы. Случай xn ≤ b рассматривается аналогично. Теорема доказана.
Замечание. Элементы сходящейся последовательности {xn} могут удовлетворять строгому неравенству xn > b, однако при этом предел a может оказаться равным b
Билет 8
Функция f(x) имеет предел A в точке x0, предельной для области определения функции f(x), если для каждой окрестности предела A существует проколотая окрестность точки x0, образ которой при отображении f(x) является подмножеством заданной окрестности точки A.
Пусть функции f1(x),f2(x),f3(x) имеют общую область задания и f1(x) ≤f2(x) ≤f3(x). Тогда, если при х->c функции f1(x) и f3(x) имеют пределом число L, то и f2(x) имеет при х->с предел L.
Билет 9
Первый замечательный предел.
При вычислении
пределов выражений, содержащих
тригонометрические функции, часто
используют предел:
 называемый первым замечательным.
Читается: предел отношения синуса к
его аргументу равен единице, когда
аргумент стремится к нулю. Док – во:
называемый первым замечательным.
Читается: предел отношения синуса к
его аргументу равен единице, когда
аргумент стремится к нулю. Док – во:
 Возьмём
круг радиуса 1, обозначим радианную
меру угла МОВ через х. Пусть 0< x
<
Возьмём
круг радиуса 1, обозначим радианную
меру угла МОВ через х. Пусть 0< x
<
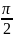 .
.
На рисунке |АМ| =
Sinх,
дуга МВ численно равна центральному
углу х, |BC|=
Tgx.
Очевидно, имеем
 .
.
На основании
соответствующих формул геометрии
получаем 1/2 Sinx
< 1/2 x
< 1/2 tgx.
Разделим неравенства на 1/2
sinx
> 0, получим 1 <
 <
<
 или Cosx
<
или Cosx
<
 < 1. Так как
< 1. Так как
 и
и
 ,
то по признаку (о пределе промежуточной
функции) существования пределов
,
то по признаку (о пределе промежуточной
функции) существования пределов

Пусть теперь x
< 0. Имеем
 ,
где –x
> 0. Поэтому
,
где –x
> 0. Поэтому

Билет 36
Ассимптоты.
 Прямая
называется асимптотой графика y=f’(x)
если расстояние от тчк. Графика до этой
прямой стремится к 0 от начала корд. При
неогр. Удалении от начала прямой.
Прямая
называется асимптотой графика y=f’(x)
если расстояние от тчк. Графика до этой
прямой стремится к 0 от начала корд. При
неогр. Удалении от начала прямой.
1)Горизонтальная
асимптота

 горизонтальная
асимптота для правой ветви графика.
горизонтальная
асимптота для правой ветви графика.

На горизонтальной асимптоте исследование проводится как для правой ветви, так и для левой
2)Вертикальные асимптоты
Точка бесконечного разрыва
X0-1точка. бесконечного разрыва

 ;
x=x0-вертикальная
ассимптота.
;
x=x0-вертикальная
ассимптота.
3)Наклонная асимптота

dcosα=γ
По усл. Наклонная асимптота kx+b что означает, что γ→0, cosα=const ↔ d→0 при x→+∞
d=f(x)-kx-b=β

Б.м.
 (1)
(1)

ф-ция отлич. От постоянной «b» на б.м. зн. Ф-ция имеет предел и он равен β

План:
Область определения ф-ции и непрерывность; тчк пересечения с осями координат; чётность, нечётность; периодичность.
Асимптоты
1-ая производная от искомой тчк критич. на экстремум
Исследование на экстремум
2-ая производная от искомой тчк. Крит на перегиб
Исследование на перегиб
График

Опре. И непрерывна (-∞; +∞)
y(0)=0
верт.
Асимптоты нет т.к. нет тчк разрыва
асимптота гориз.
 гориз. асимптоты нет.
гориз. асимптоты нет.






y=-x+2

x |
(-∞;0) |
0 |
(0,4) |
4 |
(4,6) |
6 |
(6,+∞) |
y’ |
- |
∞ |
+ |
0 |
- |
∞ |
- |
y |
↓ |
min |
↑ |
max |
↓ |
|
↓ |
