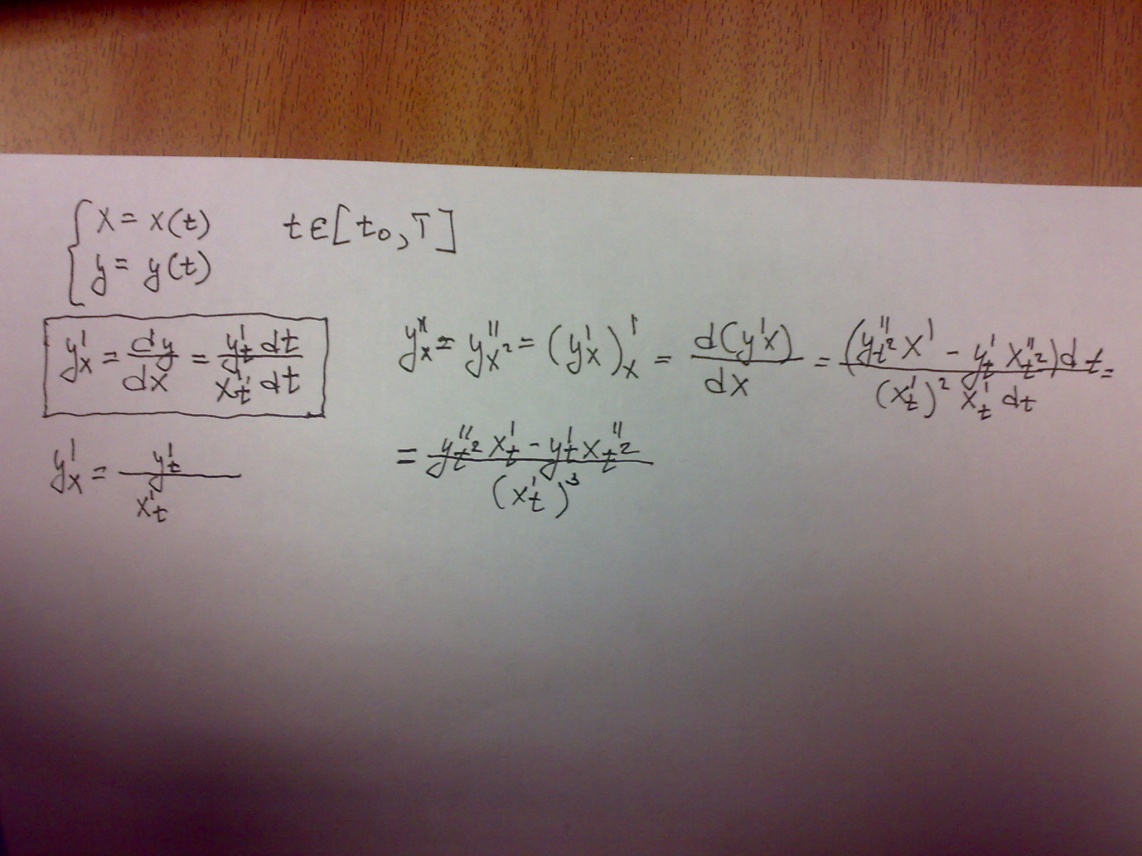Вопрос 20
Для того, чтобы функция f(x) была дифференцируема в точке x0 необходимо и достаточно, чтобы у нее существовала производная в этой точке.
При этом Δy = f(x0+Δx)-f(x0) = f '(x0)Δx+α(Δx)Δx,
где α(Δx) - бесконечно малая функция, при Δx→0.
Возьмем две точки: x и x+△x из промежутка задания функции f(x) и найдем приращение
ф-ции . если это приращение можно представить в виде: △f(x)=A(x)△x+ o(△) (△x→0)
то говорят, что ф-ция дифференцируема в точке х, а величину А(х)△х называют дифференциалом ф-ции и обозначают df(x).
Ф-ция f(x) имеет дифференциал, когда она имеет производную. Значит df(x)=f’(x)△x.
Вопрос 21
26. Дифференциал, его геометрический смысл и приложения
Возьмем две точки: x и x+△x из промежутка задания функции f(x) и найдем приращение
ф-ции . если это приращение можно представить в виде: △f(x)=A(x)△x+ o(△) (△x→0)
то говорят, что ф-ция дифференцируема в точке х, а величину А(х)△х называют дифференциалом ф-ции и обозначают df(x).
Ф-ция f(x) имеет дифференциал, когда она имеет производную. Значит df(x)=f’(x)△x.
А так
же: df(x)=f’(x)dx
и f’(x)=
Дифференциал ф-ции равен приращению, которое получает ордината касательной при переходе от точки х к точке х+dx.
Замена приращения ф-ции дифференциалом означает замену с достаточно высокой степенью точности малого отрезка кривой малым отрезком прямой линии.
Такая замена приводит к очень простой связи приращения ф-ции с приращением аргумента: приращение ф-ции оказывается прямо пропорциональным приращению аргумента. Это позволяет решить огромное число задач, кажущихся неразрешимыми
Итак, если x является независимой переменной, то дифференциал функции y=f(x) можно
записать так: dy=f’(x)dx.
Покажем, что эта форма сохраняется и в случае, если x является не независимой
переменной, а функцией. Действительно, пусть y=f(x) и x=(t), то есть y – сложная
функция от t: y=f[(t)]. Тогда, dy=y’tdt
По правилу дифференцирования сложной функции: y’t=y’x*x’t. .Отсюда dy=y’x*x’tdt=y’xdx=f’(x)dx.
Этим мы доказали следующее:
Теорема. Дифференциал сложной функции y=f(x), для которой x=(t), имеет такой же вид,
dy=f’(x)dx, как и в том случае, когда аргумент x является независимой переменной. Это
свойство называется – инвариантность формы дифференциала
Приближенное
вычисление.
Вопрос 22
Вопрос 23
Вопрос 24
Параметрическое задание линий
На промежутке [a, b] заданы две непрерывные функции U(t), V(t). Множество точек на плоскости с координатами:
X=U(t) t∈[a,b]
Y=V(t)
Называем линией на плоскости.
Аргумент, от которого зависят координаты, называют параметром линии, а способ задания линии называют параметрическим.
Одна и та же линия может иметь различные параметрические задания.
Пример:
Параметрическое ур прямой, проход через точку (x₀, y₀), с направляющ вектором(l, m):
X=lt + X₀ t∈R
Y=mt + Y₀
Вопрос 25
25)Производная функция задана параметрически
Если
на линии:
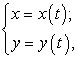каждому
значению х отвечает одно-единственное
значение y, то мы будем
говорить, что y является
параметрически заданной функцией от
х.
Y’x=Y’t/X’t
Y”x=Y”x^2=d(Y’X)/d(X)=(Y”t^2*X’-Y’t*X”t^2)dt/(((X’t)^2)*X’t*dt=(Y”t^2*X’t-Y’t*X”t^2)/((X’t)^3)
Yxk=dy(k-1)/dx
