16 Волновое уравнение

Волновое уравнение, дифференциальное уравнение с частными производными, описывающее процесс распространения возмущений в некоторой среде. В случае малых возмущений и однородной изотропной среды В. у. имеет вид:

  

где х, у, z — пространственные переменные, t — время, u = u (х, у, z) — искомая функция, характеризующая возмущение в точке (х, у, z) в моментt, а — скорость распространения возмущения. В. у. является одним из основных уравнений математической физики и широко используется в приложениях. Если u зависит только от двух (одной) пространственных переменных, то В. у. упрощается и называется двумерным (одномерным). В. у. допускает решение в виде "расходящейся сферической волны":

  u = f (t - r/a)/r,

где f — произвольная функция, a

  

  Особый интерес представляет так называемое элементарное решение (элементарная волна):

  u = δ (t - r/a)/r

(где δ — дельта-функция), дающее процесс распространения возмущения, произведённого мгновенным точечным источником (действовавшим в начале координат при t = 0). Образно говоря, элементарная волна представляет собой "бесконечный всплеск" на окружности r = at, удаляющийся от начала координат со скоростью а с постепенным уменьшением интенсивности. При помощи наложения элементарных волн можно описать процесс распространения произвольного возмущения.

Формула Д'Аламбера

Решение одномерного волнового уравнения

 (функция f(x,t) соответствует вынуждающей внешней силе)

с начальными условиями

имеет вид

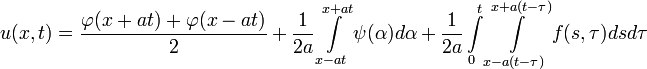
17  Энергия электромагнитной волны

Объемная плотность энергии электромагнитного поля в линейной изотропной среде равна сумме объемных плотностей энергии электрического и магнитного полей, поэтому

 

 ,

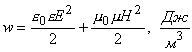
где v - скорость распространения электромагнитной волны в среде.

В случае плоской линейно поляризованной монохроматической волны объемная плотность энергии волны

 

т.е значение w в каждой точке поля периодически изменяется от 0 до w_макс=Е₀Н₀/v за промежуток времени .

Пло́тность пото́ка эне́ргии — физическая величина, численно равная потоку энергии через единичную площадку, перпендикулярную направлению потока. Часто вводят также вектор плотности потока энергии (так называемый вектор Умова), величина которого равна плотности потока энергии, а направление совпадает с направлением потока. В электродинамике вектор плотности потока электромагнитной энергии носит название вектора Пойнтинга.

 (в системе СИ),

где E и H — векторы напряжённости электрического и магнитного полей соответственно.

 (в комплексной форме)

18 Волновое сопротивление — характеристика среды распространения волнового возмущения.

• В акустике: в газе и жидкости — отношение звукового давления в бегущей плоской звуковой волне к колебательной скорости частиц среды, оно равно произведению плотности среды на скорость звука в ней; в твёрдых телах для продольных волн волновое сопротивление — отношение механического напряжения, взятого с обратным знаком, к колебательной скорости частиц среды. См. также статью удельное акустическое сопротивление.

• В гидромеханике — часть гидро- и аэродинамического сопротивления, характеризующая затрату энергии на образование волн, например, волн, образующихся на поверхности воды при движении корабля, ударных волн, возникающих при сверхзвуковом полете самолёта, и т. д.

• В электродинамике волновое сопротивление линий передачи — отношение амплитуды напряжения бегущей волны к амплитуде силы тока бегущей волны. (Бегущие волны могут присутствовать и в других режимах) Зависит от таких параметров линии, как ёмкость, диэлектрическая проницаемость материала проводника (зависит от частоты работы генератора сигнала), индуктивность и сопротивление на единицу длины.

Справедливо для волнового сопротивления в длинных линиях:

, где

 — волновое сопротивление линии,  — амплитуда напряжения в линии,  — амплитуда силы тока в линии,

В бесконечно длинных линиях нагрузка имеет чисто активный характер, поэтому энергия, запасаемая в индуктивности и ёмкости, одинаковая.

, где

 — погонная индуктивность,  — погонная ёмкость,  — часть линии,  — амплитуда напряжения в линии,  — амплитуда силы тока в линии,

Поэтому волновое сопротивление в бесконечно длинных линиях определяется погонными индуктивностью и ёмкостью:

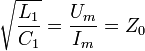
Волновое сопротивление среды — отношение амплитуд электрического и магнитного полей электромагнитных волн, распространяющихся в среде:

19 Если волновое сопротивление двух сред, имеющих границу раздела, одинаковы, то на этой границе не происходит отражения электромагнитных волн, даже если диэлектрическая и магнитная проницаемости в средах различны.

20 Интерференция волн — взаимное усиление или ослабление амплитуды двух или нескольких когерентных волн, одновременно распространяющихся в пространстве. Сопровождается чередованием максимумов и минимумов (пучностей) интенсивности в пространстве. Результат интерференции (интерференционная картина) зависит от разности фаз накладывающихся волн.

Колебания когерентны, если разность их фаз постоянна во времени и при сложении колебаний получается колебание той же частоты.

При интерференции энергия волн перераспределяется в пространстве. Это не противоречит закону сохранения энергии потому, что в среднем, для большой области пространства, энергия результирующей волны равна сумме энергий интерферирующих волн.

Стоя́чая волна́ — колебания в распределённых колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов)амплитуды. Практически такая волна возникает при отражениях от преград и неоднородностей в результате наложения отражённой волны на падающую. При этом крайне важное значение имеет частота, фаза и коэффициент затухания волны в месте отражения.

Чисто стоячая волна, строго говоря, может существовать только при отсутствии потерь в среде и полном отражении волн от границы. Обычно, кроме стоячих волн, в среде присутствуют и бегущие волны, подводящие энергию к местам её поглощения или излучения.

21 ДИСПЕРСИЯ ВОЛН (от лат. dispersio — рассеяние), зависимость фазовой скорости v_ф гармонич. волны от её частоты w. Простейшим примером явл. Д. в. в линейных однородных средах, характеризуемая т. н. дисперс. уравнением (законом дисперсии); оно связывает частоту и волн. число k плоской гармонич. волны: w=w(k) (а в анизотропных средах — частоту и волн. вектор k). Дисперс. уравнение может иметь неск. ветвей, к-рым соответствуют разл. типы волн (моды). Напр., в изотропной плазме — это ветви, относящиеся к эл.-магн., плазменным и ионно-звук. волнам.

В линейных средах Д. в. всегда приводит к размыванию волн. возмущения (см. Групповая скорость, Волновой пакет); при наличии нелинейности возможно конкурирующее сжатие волн. пакета. В результате могут возникать стационарные нелинейные волны, как периодические, так и уединённые (напр., солитоны)

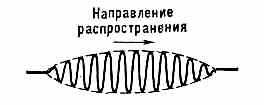
ГРУППОВАЯ СКОРОСТЬ, скорость движения группы или цуга волн, образующих в каждый данный момент времени локализованный в пр-ве волновой пакет (рис. 1). В линейных средах, где соблюдается суперпозиции принцип, его можно рассматривать

как набор гармонич. волн с частотами в интервале w₀-Dw<w<w₀+Dw тем более узком, чем плавнее и протяжённее огибающая группы. Длина пакета DL и его спектр. полоса Dw ограничены снизу соотношением DLDk³1, где волновое число k связано с частотой со дисперсионным соотношением w=w(k) (см. Дисперсия волн).

Если среда не обладает дисперсией, то все гармонич. волны распространяются с одной и той же фазовой

22 Используя Гаусса - Остроградского формулу и С такса формулу, ур-ниям (1) - (4) можно придать форму интегральных:

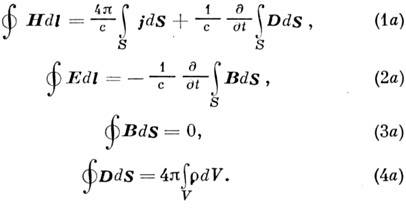
Уравне́ния Ма́ксвелла — система дифференциальных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах. Вместе с выражением для силы Лоренца образуют полную систему уравнений классической электродинамики. Уравнения, сформулированные Джеймсом Клерком Максвеллом на основе накопленных к середине XIX века экспериментальных результатов, сыграли ключевую роль в развитии представлений теоретической физики и оказали сильное, зачастую решающее, влияние не только на все области физики, непосредственно связанные с электромагнетизмом, но и на многие возникшие впоследствии фундаментальные теории, предмет которых не сводился к электромагнетизму (одним из ярчайших примеров здесь может служить специальная теория относительности).

ТОК СМЕЩЕ́НИЯ, величина, пропорциональная скорости изменения переменного электрического поля в диэлектрике или вакууме. Название «ток» связано с тем, что ток смещения, так же как и ток проводимости, порождает магнитное поле

Понятие ток смещения введено Максвеллом для установления количественных соотношений между изменяющимся электрическим полем и вызываемым им магнитным полем.  В соответствии с теорией Максвелла, в цепи переменного тока, содержащей конденсатор, переменное электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле, какое создавал бы ток, (названный током смещения), если бы он протекал между обкладками конденсатора. Из этого определения следует, что J_см = J (т. е., численные значения плотности тока проводимости и плотности тока смещения равны), и, следовательно, линии плотности тока проводимости внутри проводника непрерывно переходят в линии плотности тока смещения между обкладками конденсатора. Плотность тока смещения j_см характеризует скорость изменения электрической индукции

Электромагнитная волна - процесс распространения электромагнитного поля в пространстве. Электромагнитная волна представляет собой процесс последовательного, взаимосвязанного изменения векторов напряжённости электрического и магнитного полей, направленных перпендикулярно лучу распространения волны, при котором изменение электрического поля вызывает изменения магнитного поля, которые, в свою очередь, вызывают изменения электрического поля.

 скорость распространения Э. в. в вакууме равна скорости света, Максвелл сделал вывод, что свет представляет собой Э. в. 

В изотропном пространстве скорость распространения гармонических Э. в., т. e. фазовая скорость 

Бегущая электромагнитная волна описывается следующими формами E_y' = E₀sin[k(x–ct)] H_z' = E₀sin[k(x–ct)] и E_y'' = E₀sin[k(x+ct)] H_z'' = E₀sin[k(x+ct)+π]

23 Электромагнитные волны переносят энергию из одной точки пространства в другую за конечное время из-за конечности скорости распространения электромагнитной волны, равной , как мы убедились выше, скорости света в той среде, где она распространяется.

Энергия   электромагнитной волны внутри некоторого объёма   определяется плотностью энергии   электромагнитного поля волны в соответствии с выражением¹:

.

Оказывается плотность энергии электромагнитной волны находится в связи с плотностью потока энергии, импульса, связанных с феноменом давления электромагнитных волн.

Рассмотрим определение плотности энергии электромагнитной волны.

Пусть среда, в которой распространяется электромагнитная волна, не является ферромагнетиком или сегнетоэлектриком, неподвижна и не обладает проводимостью ( ) . В этом случае можно считать равными нулю токи проводимости, поскольку в соответствии с законом Ома эти токи пропорциональны проводимости:  . Вследствие этого нет расхода части энергии электромагнитной волны на увеличение внутренней энергии среды распространения волны из-за выделения Джоулева тепла.

В частном случае однородных сред распространения в соответствии с материальными уравнениями   и объёмная плотность энергии электромагнитной волны может быть рассчитана по формуле

.

Или в другом виде

.

Вектор Пойнтинга (также вектор Умова — Пойнтинга) — вектор плотности потока энергии электромагнитного поля, одна из компонент тензора энергии-импульса электромагнитного поля. Вектор Пойнтинга S можно определить через векторное произведение двух векторов:

 (в системе СГС),

 (в системе СИ),

где E и H — векторы напряжённости электрического и магнитного полей соответственно.

 (в комплексной форме)^[1],

где E и H — векторы комплексной амплитуды электрического и магнитного полей соответственно.

Этот вектор по модулю равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии.

Поскольку тангенциальные к границе раздела двух сред компоненты E и H непрерывны (см. граничные условия), то вектор S непрерывен на границе двух сред.

24 Стоячая электромагнитная волна представляет собой электромаг­нитную волну, полученную в результате наложения движущихся навстречу падающей и отраженной электромагнитных волн одинаковой интенсивности.

Стоячая электромагнитная волна образована стоячими волнами напряжения и тока. Математически такие волны описываются произ­ведением двух периодических (в нашем случае – тригонометрических) функций. Одна из них – функция координаты текущей точки на линии (в нашем случае bу), другая – функция времени (wt). Стоячие волны напряжения и тока всегда сдвинуты по отношению друг к другу в пространстве и во времени.

Сдвиг во времени между стоячими волнами напряжения и тока равен 90°, сдвиг в пространстве-четверти длины волны. Точки линии, где периодическая функция координаты проходит через нуль, называют узлами, а точки линии, в которых периодическая функция координаты прини­мает максимальные значения, – пучностями.

П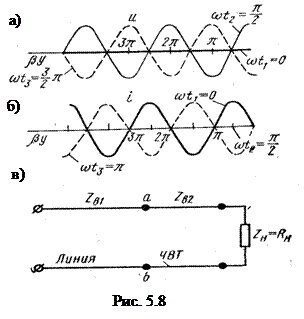 ри возникновении стоя­чих волн электромагнитная энергия от начала к концу линии не передается. Однако на каждом отрезке линии, равном четверти длины вол­ны, запасена некоторая элек­тромагнитная энергия. Эта энергия периодически переходит из одного вида (энергии электрического поля) в другой (энергию магнитного поля).

В моменты времени, когда ток вдоль всей линии оказы­вается равным нулю, а напря­жение достигает максималь­ного значения, вся энергия переходит в энергию электри­ческого поля.

В моменты времени, когда напряжение вдоль всей линии равно нулю, а ток достигает максимального значения, вся энергия переходит в энергию магнитного поля.