17. Динамические показатели качества сау.

Рассмотрим динамические показатели авт. Систем, описываемых уравнением

A(p)y=0

Или

^x=Ax x₀=x(0) (2)

^y=Cx y₀=y(o) (3)

Решение уравнения 2 и 3 будет записываться в виде

X(t)=e^Atx₀ (4)

Y(t)=Ce^Aty₀ (5)

Решениями уравнений 4 и 5 соотв. Свободной составляющей y_св(t) и x_св(t) (возмущ. системы)

Для устойчивой авт. Системы должны выполнятся условия устойчивости

X(t)-> 0

Y(t)-> 0

Д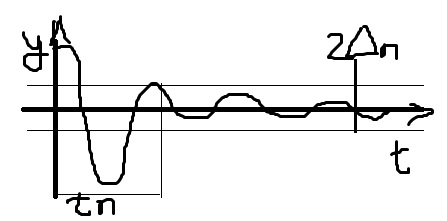 ля анализа динамических свойств вводят в рассмотрение динамические показатели качества, т.е. численные оценки быстродействия и колебательности системы

А) Время переходного процесса (t_п)

t_п-время, за которое система входит в дельта окрестность навсегда; дельта=δ_п|y_y|;

δ_п=0,05

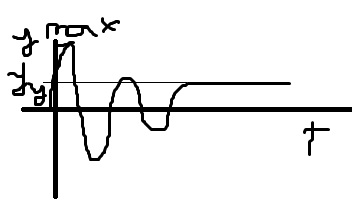
Б) Перерегулирование

_δ=|y_max-y_y/y_y|*100%

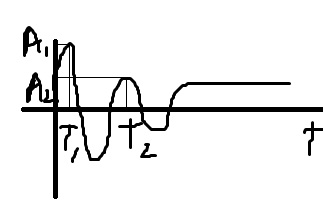
В) Затухание

ξ=(A₁-A₂)/A₁

A₁=y(t₁)

A₂=y(t₂)

18.Точностные характеристики сау. Определение установившейся ошибки.

Установившаяся ошибка представляет собой функцию времени, удовлетворяющую условию

для любых начальных условий и заданного входного воздействия . Другими словами, она характеризует ошибку слежения, установившуюся после завершения переходного процесса.

Для приближенной оценки установившейся ошибки слежения при произвольном (но достаточно гладком) входном воздействии можно воспользоваться следующей методикой. Разложим в ряд Тейлора в окрестности точки

, где , . Тогда получаем выражение установившейся ошибки при произвольном входном воздействии

, где постоянные носят название коэффициентов ошибок. Если изменяется достаточно медленно, то для приближенной оценки можно использовать конечное число членов ряда.

19.Точностные характеристики сау. Расчет предельного значения ошибки.

Предельное значение установившейся ошибки определяется выражением

Величина предельного значения установившейся ошибки при типовом задающем воздействии может быть достаточно просто рассчитана по передаточной функции системы. Пусть образы Лапласа ошибки слежения и сигнала задания связаны соотношением

, где — известная передаточная функция замкнутой системы по ошибке слежения (относительно задающего воздействия). Например, для систем с единичной отрицательной обратной связью имеем

, где — передаточная функция разомкнутой системы, включающая в себя передаточные функции регулятора и объекта управления. Тогда, в соответствии с теоремой о предельном переходе во временной области, имеем .

20.Точностные характеристики сау. Понятие астатизма.

В качестве универсальной характеристики точностных свойств систем управления используется понятие порядка астатизма (по отношению к входному воздействию). Система называется статической (или — с нулевым порядком астатизма), если в выражении . Говорят, что система имеет k-й порядок астатизма, если в выражении для всех и .

Для систем с единичной отрицательной обратной связью порядок астатизма может быть достаточно просто определен на основе анализа структурных свойств системы. Так, система на рис.7.1 является статической (т.е. с нулевым порядком астатизма), если

, где — общий коэффициент усиления разомкнутой системы.

Передаточная функция разомкнутой системы может быть представлена в виде

, где — передаточная функция статической системы (т.е. ). При этом число соответствует порядку астатизма.