13. Устойчивость сау. Типы устойчивости.

Под устойчивость системы САУ понимается способность системы возвращаться в исходное положение равновесия после прекращения входного сигнала.

Типы:

У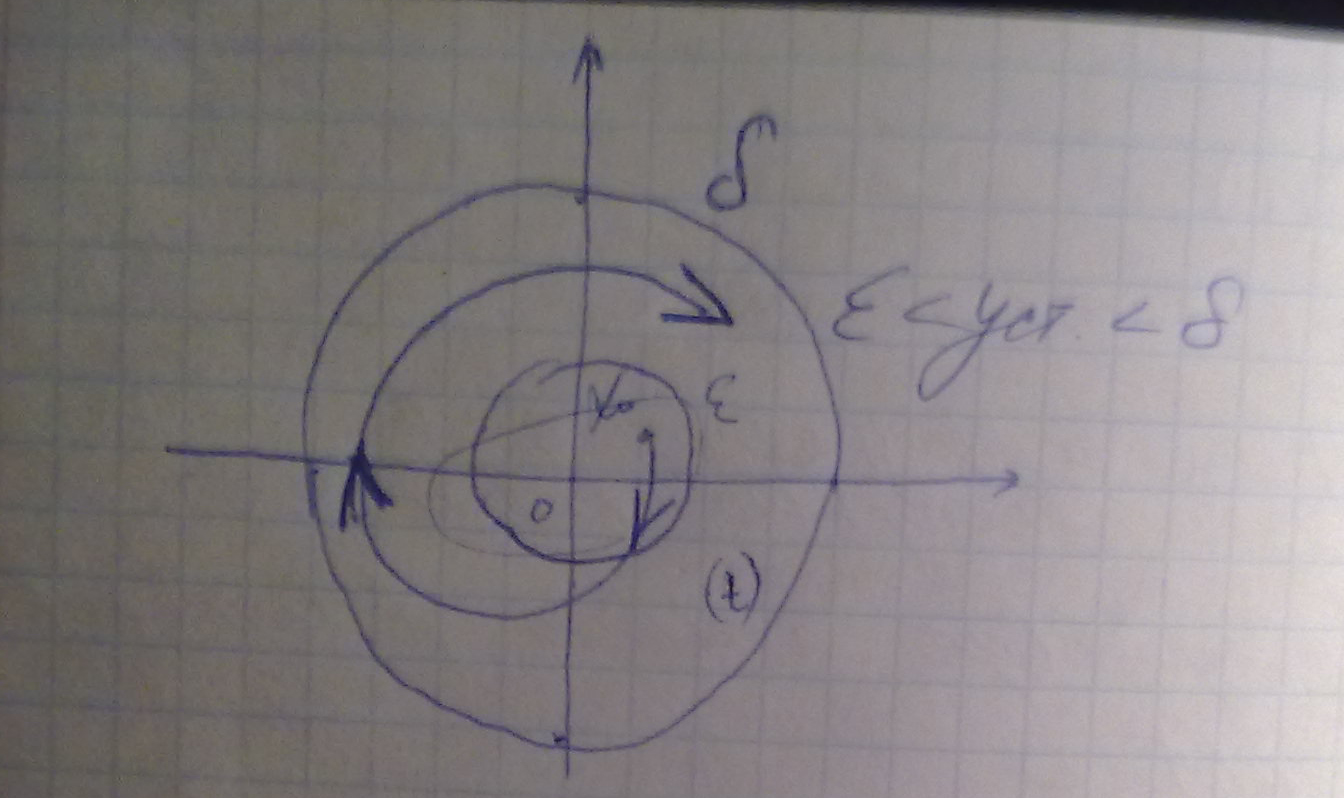 стойчивость по Ляпунову

Будем говорить, что положение равновесия x=0 устойчиво по Ляпунову, если для любых траекторий движения x(t), порождаемых н.у. x(0) ограниченными неравенством ||x(0)||<=ε ε>0 , существует δ> ε, для которой ||x(t)||<=δ

||x||=sqrt(x₁²+x₂²+…+x_n²)

А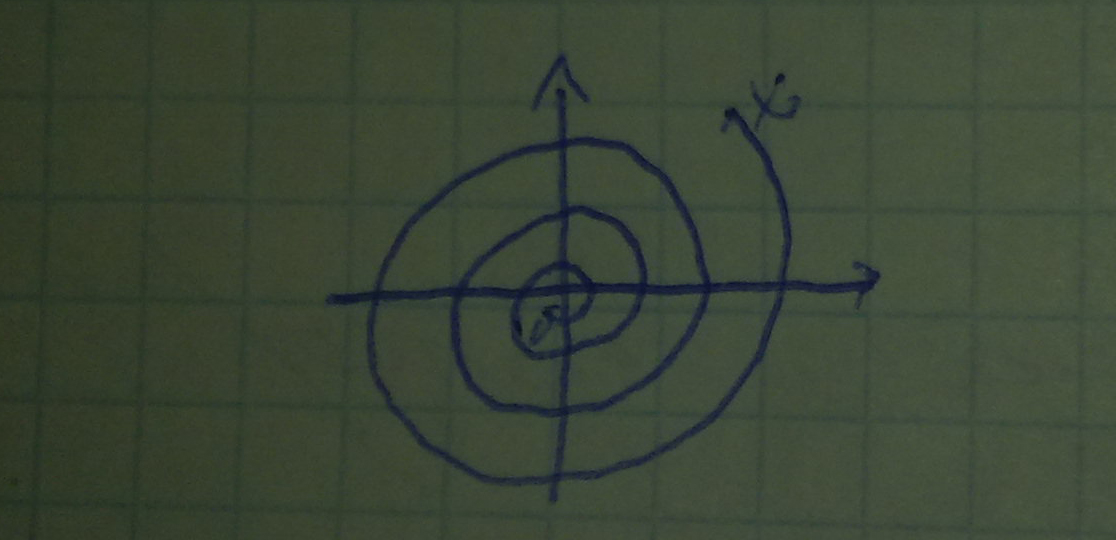 симптотическая устойчивость

Будем говорить, что положение x=0 асимпт. Устойчиво, если оно устойчиво по Ляпунову и для любых траекторий движения, поражденных произвольными н.у. верно высказывание lim(t->inf) ||x(t)||=0

Экспоненциальная устойчивость

Будем говорить, что x=0 экспоненциально устойчиво, еcли для всех траекторий x(t), порожденных произвольными н.у. существуют такие

_β>=1 α>0

что для любого момента времени справедливо нерав.

||x(t)||<= β*e^-αt||x(0)||

Окрестность Н.У. ||x(0)||<C₀ (C₀ >0- окрестность)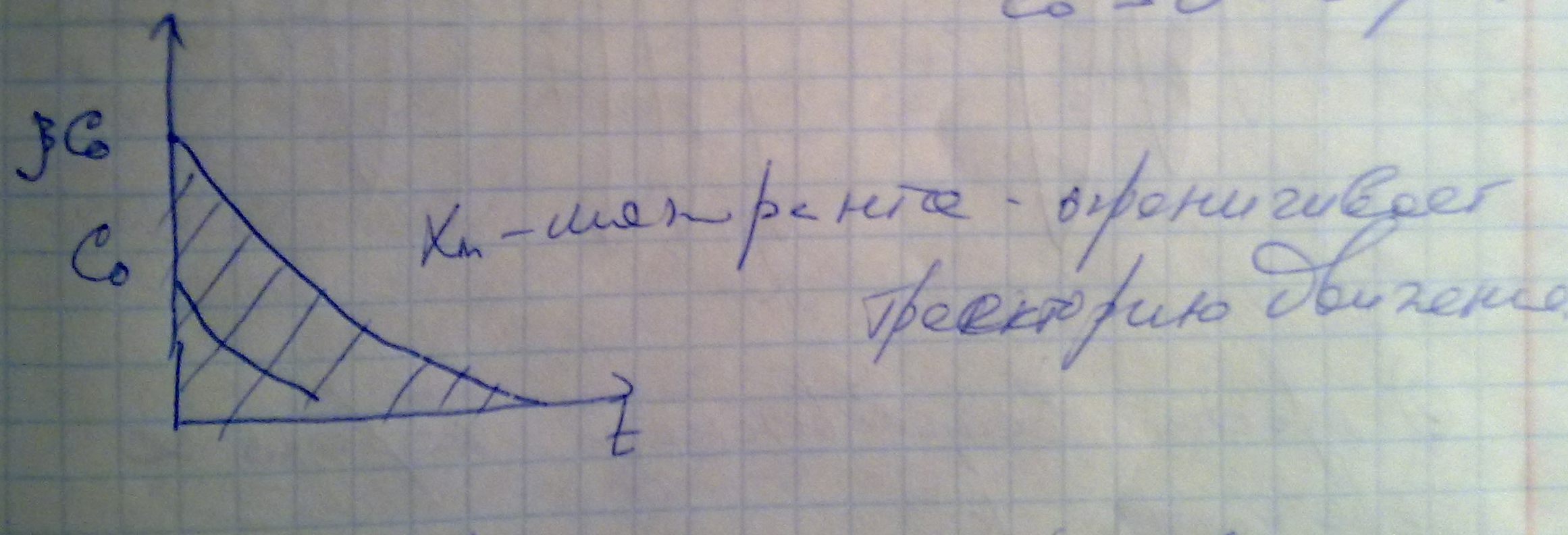

14. Устойчивость сау. Корневой критерий устойчивости.

Простой вещественный корень α

Y_св(t)=Ce^αt…….3 графика C(t)

1. Возрастающий – неуст

2. Постоянн – по Ляпунову

3. Падает экспоненц. уст

Пара комплексно сопряженных корней

Y_cв(t)=Ae^αtsin(βt+ψ)

3 колеблящихся (торнадо) графика y_св(t)

1. Увели – неуст

2. Const(sint) – по ляпунову

3. Торнадо асимптот.

Простой вещественный корень α кратности k

Y_св=C₁e^αt+C₂te^{αt^2}+C₃t^2e^{αt^3}+…+

_α>0 y_св(t)->inf – система неустойчива

_α=0 y_св(t)->inf – система неустойчива

_α<0 y_св(t)->0 – система устойчива асимптотически

Пара комплексно сопряженных корней кратности k

Y_св(t)=A₁e^αt(sinβt+ψ)+A₂te^{αt^2}(sinβt^2+ψ)…

_α>0 y_св->inf – не устойчива

_α=0 y_св->inf – не устойчива

_α<0 |y_св|->inf – асимптотически устойчива

Для того, чтоюы система была устойчива необходимо, чтобы все корни характерист. Уравнения были не кратными и имели отрицательную вещественную часть. Если хоть один корень имеет положительную вещественную часть -> неустойчива.

15. Устойчивость сау. Алгебраический критерий устойчивости.

Знаменатель – D(p)=pⁿ+a_n-1p^n-1+…+a₀p+a₀

Линейная система с характеристическим уравнением ^ будет асимптотически устойчива, если все диагональные определители матрицы Гурвеца положительны. Если хоть один – отрицательный, то неустойчива. Если хоть один =0 устойч. По Ляпунову. Для систем начиная с 3 порядка кроме положительности коэффициентов должно выполнятся еще одно соотношение (произведение крайних членов знаменателя передаточной функции должно быть меньше произведению средних)

16. Управляемость и наблюдаемость систем управления.

Линейная система полностью управляема, если для любых t0 ≥ 0 и xf ∈

R^n существует tf ≥ t◦ и ограниченное управление u(t), t ∈ [t0, tf ] такое, что для x(t0) = x0 выполняется x(tf) = xf .

1) Для линейных систем это означает, что любое состояние достижимо из любого другого.

2) Если управляемая линейная система стационарна, то попадание в xf можно обеспечить за любое заданное времяT > 0 (T = tf−t0)

3) Свойство управляемости не зависит от выходной переменной y и поэтому может быть определено как свойство модели.

матрица управляемости размерности n × n

U = |B : AB : A^2 B...A^n−1 B|

Система полностью управляема тогда и только тогда, когда ранг матрицы управляемости равен порядку системы, т.е. rankU = n.

Система полностью управляема тогда и только тогда, когда матрица управляемости не вырождена, т.е. detU не равен 0.

Система полностью управляема тогда и только тогда, когда она может быть преобразована к канонической управляемой форме.

Системы, в которых матрица входа равна нулю (B = 0) с очевидностью являются неуправляемыми.

Система называется полностью наблюдаемой, если для любых t◦ ≥ 0 существует t1 > t0 такое, что выходной переменной y = y(t), t ∈ [t0, t1] полученной для входного сигнала u(t), соответствует единственное значение x(t0) = x0.

1) Для стационарной наблюдаемой линейной системы значение x(t0) можно определить за любое заданное время T > 0 (T =t1 – t0).

2) Т.к. наблюдаемость, если она есть, должна быть при нулевом входе, можно считать, что система наблюдаема, если для неё по y[t0,t1] можно однозначно определить x(t0) при u(t) = 0.

Для анализа наблюдаемости линейных систем используется матрица наблюдаемости размерности n × n:

Q = | C |

| CA |

| CA^2 |

| : |

|CA^n−1 |

Система полностью наблюдаема тогда и только тогда, когда матрица наблюдаемости не вырождена, т.е. detQ не равен 0.

Система полностью наблюдаема тогда и только тогда, когда матрица наблюдаемости имеет ранг, который совпадает с порядком ОУ, т.е. rankQ = n.

Система полностью наблюдаема тогда и только тогда, когда она может быть преобразована к канонической наблюдаемой форме.