11. Типовые динамические звенья второго порядка и их характеристики.

Апериодическое звено 2-го порядка описывается дифференциальным уравнением:

или ,

где - постоянные времени, причем . При этом корни характеристического уравнения будут вещественными и отрицательными.

Знаменатель передаточной функции апериодического звена 2-го порядка разлагается на множители:

,

где ,

Апериодическое звено второго порядка эквивалентно двум звеньям первого порядка, включенным последовательно друг за другом, с общим коэффициентом усиления и постоянными времени . Его переходная функция имеет вид

.

Колебательное звено описывается тем же дифференциальным уравнением, что и апериодическое звено второго порядка. Однако корни характеристического уравнения должны быть комплексными, что будет выполняться при .

Передаточная функция колебательного звена обычно представляется в виде

,

где - период свободных колебаний при отсутствии затухания, - параметр затухания, лежащий в пределах . Переходную функцию данного звена можно представить в виде

,

где , . Параметр легко определяется по графику переходной функции, а параметр находится посредством выражения

.

Интегрирующее звено с замедлением описывается дифференциальным уравнением:

или

где - постоянная времени, а его переходная функция

.

Консервативное звено является частным случаем колебательного звена при . Тогда корни характеристического уравнения будут чисто мнимые. Передаточная функция колебательного звена имеет вид

,

а его переходная функция - ,

где .

12. Типовые включения динамических блоков. Правила преобразования структурных схем.

Под структурной схемой СУ понимается графическое изображение СУ, в которой каждый элемент схемы изображается в виде блока с указанием входной и выходной переменной, внутри блока записывается передаточная функция, связывающая входную и выходную переменную, и, кроме того, указываются все связи между элементами системы.

Графические элементы.

1. T 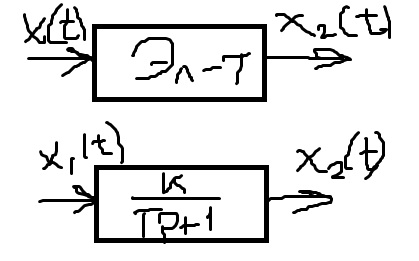*dx₂/dt+x₂=kx

P=d/dt; T*x₂p+x₂=kx₁

W(p)=x₂(p)/x₁(p)= k/(Tp+1)

2. Э 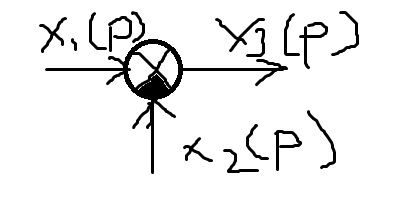л-т сравнения

X₃(p)=x₁(p)-x₂(p)

3. С 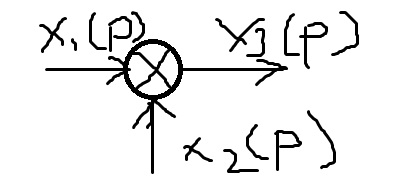умматор

X₃(p)=x₁(p)+x₂(p)

Последовательное соединение элементов

Е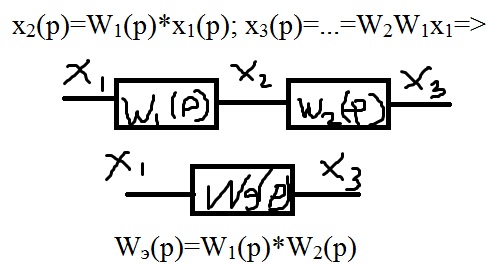 сли в системе есть k посл. Элементов, то экв. Передаточная функция определяется произведением передаточных элементов.

Параллельное соединение

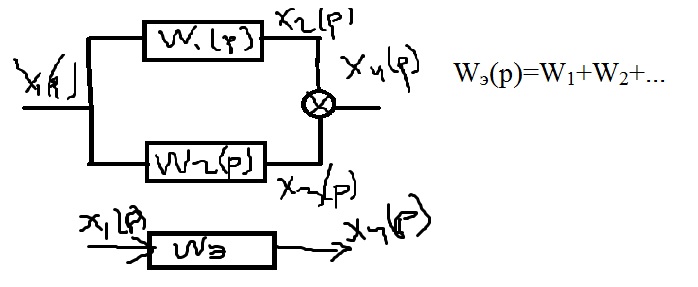
Соединение с ООС

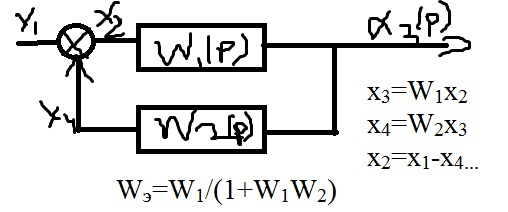
Соединение с ПОС

Последовательность структурных преобразований

1. На структурной схеме для каждого элемента вводятся обозначения входных и выходных переменных.

2. Для каждого из элементов структурной схемы составляется уравнение связи между выходной и входной переменными. Полученная система уравнений задаёт описание всей структурной схемы. Число уравнений соответствует числу структурных элементов.

3. Последовательной подстановкой одного уравнения в другое исключаются промежуточные переменные, пока не останется уравнение связи между интересующими нас переменными, по которому и отыскивается искомая передаточная функция.