
- •2.Принцип относительности Галилея. Преобразования Галилея.
- •3. Законы Ньютона. Методы решения задач в мех Ньютона.
- •4. Теоремы об изменении импульса и момента импульса.
- •5.Свойства потенциальных полей
- •6.Теорема об изменении кинетической энергии материальной точки.
- •7.Теорема об изменении импульса механ. Системы.
- •8. Выделение движения центра масс и относительного движения механической системы.
- •9. Теорема об изменении момента импульса механической системы.
- •10. Теорема об изменении кинетической энергии механической системы.
- •17. Общее ур-е механики.
- •18. Решение задачи о движении тела по наклонной плоскости в поле сил тяжести на основании ур-я Лагранжа 1го рода.
- •21.Вариационный принцип.
- •22.На основании ур-я Лагранжа-Эйлера получить ур-я колебаний метем. Маятника и колеб. Точки под упругой силы.
- •27. Решение задачи Кеплера в формализме Лагранжа.
- •28. Законы Кеплера.
- •29. Основные элементы описания линейных многомерных колебаний в формализме Лагранжа.
- •30.Уравнения колебаний многомерной системы в формализме лагранжа в линейном приближении.
- •31 Определение собственных частот многомерн.Колеб в лин.Приблежении.
- •41. Законы сохранения физических величин в формализме Гамильтона
- •42. Фазовое пространство. Закон сохранения потока точек фазового пространства
- •46. Движение заряженной частицы в электромагнитном поле в формализме Лагранжа
- •47. Движение заряженной частицы в электромагнитном поле в формализме Гамильтона
1.Осн. пон-я теор. физ.
Классич.
механ. заним-ся движен. микроскоп. тел,
скорости к-ых много меньше скор. света.
Материал (.)(частица) – размер котор.
можн. пренебр., по сравнению с разн.
характер-е это тело,или (.) обладающ.массой.
Положением мат. (.) и в прост-ве зад-ся в
опред. выбран. системе координат. В клас.
мех. реализ. в 3х мерной и евклидово = >
 Расстояние
между 2мя (.) и не измен. при повороте
системы координат или при перем. нач.
системы отсчета. Событие обозначается
местом и моментом. Совокупность событий
образ. многообраз. 4х мерн. пространства
времени. В класич. мех. это 4х мерн. многобр
расчепл. на 3х мерный евклид и ось. В
класич. мех. св-ва 3х мерн. простр. не
завис. от св-в времени. Расстояние между
(.) и измерения независимо, т.е. св-ва
пр-ва и времени не связ. др. с др., но это
спр. не в реалит. Поскольку время и пр-во
отделили друг от друга механ., то можно
в этом случае ввести понятие абс. пр-ва
и абс вр-ни: время вступает как пар-р, а
радиус – вектор зав. y(t),z(t),x(t),
Расстояние
между 2мя (.) и не измен. при повороте
системы координат или при перем. нач.
системы отсчета. Событие обозначается
местом и моментом. Совокупность событий
образ. многообраз. 4х мерн. пространства
времени. В класич. мех. это 4х мерн. многобр
расчепл. на 3х мерный евклид и ось. В
класич. мех. св-ва 3х мерн. простр. не
завис. от св-в времени. Расстояние между
(.) и измерения независимо, т.е. св-ва
пр-ва и времени не связ. др. с др., но это
спр. не в реалит. Поскольку время и пр-во
отделили друг от друга механ., то можно
в этом случае ввести понятие абс. пр-ва
и абс вр-ни: время вступает как пар-р, а
радиус – вектор зав. y(t),z(t),x(t),
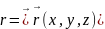 Если
бы вы рассм. пр-во как единое, то
x{x,y,z,ct}.
Механическое движение-изменение с теч.
Времени взаимного пол-я в пр-ве мат. тел.
Тело отсчета - тело, относит к-ого опред.
событие связан. с др. телами. Тель отсчёта:
СК с началом совмещ. с телом отсчет и
часы в сов-ти обр. систему отсчета.
Механическая система - сов-ть материал.(.)
и в неретешивис. массы мех.сис-мы масс
матер. (.)ы. Состояния мех. системы опред.
заданием всех коорд. матер. (.) и в данный
момент. Основная задача механики состоит
в том, что бы по заданию в данный момент
времен. состояния опред. сост. Решить
осн. задачу: означ. опред. дв-е сис-мы,
т.е. опред.x(t),y(t),z(t)
в данный момент времени: x(t),y(t)
и z(t)
сост. реш-е ур-е дв-е в виде ДУ т. обр.
решить задачу механическим означ:
1)получить вид ур-я дв-я мех. сис-мы.
2)решить эти ур-я, что бы получ. зав. корд.
от времени. Положен. Матер. (.)в данный
момент времени опред. с пом. µ конец рад.
при дв-е мат. (.) опис. в пр-ве кривую, наз.
траекторией т. обр. Траектория-геом.
место положения движения мат.(.) в опред.
сис-ме отсчета. Инертность-свойство
мат. тела сохр. сост-я покоя равн. или
прямого действия. Инерц. СО – Со относит.
к-ой мат.(.) движ. Равном и прямолинейном
2 СО наз. инерциал., если они движ. с Const
скоростями.
Если
бы вы рассм. пр-во как единое, то
x{x,y,z,ct}.
Механическое движение-изменение с теч.
Времени взаимного пол-я в пр-ве мат. тел.
Тело отсчета - тело, относит к-ого опред.
событие связан. с др. телами. Тель отсчёта:
СК с началом совмещ. с телом отсчет и
часы в сов-ти обр. систему отсчета.
Механическая система - сов-ть материал.(.)
и в неретешивис. массы мех.сис-мы масс
матер. (.)ы. Состояния мех. системы опред.
заданием всех коорд. матер. (.) и в данный
момент. Основная задача механики состоит
в том, что бы по заданию в данный момент
времен. состояния опред. сост. Решить
осн. задачу: означ. опред. дв-е сис-мы,
т.е. опред.x(t),y(t),z(t)
в данный момент времени: x(t),y(t)
и z(t)
сост. реш-е ур-е дв-е в виде ДУ т. обр.
решить задачу механическим означ:
1)получить вид ур-я дв-я мех. сис-мы.
2)решить эти ур-я, что бы получ. зав. корд.
от времени. Положен. Матер. (.)в данный
момент времени опред. с пом. µ конец рад.
при дв-е мат. (.) опис. в пр-ве кривую, наз.
траекторией т. обр. Траектория-геом.
место положения движения мат.(.) в опред.
сис-ме отсчета. Инертность-свойство
мат. тела сохр. сост-я покоя равн. или
прямого действия. Инерц. СО – Со относит.
к-ой мат.(.) движ. Равном и прямолинейном
2 СО наз. инерциал., если они движ. с Const
скоростями.
2.Принцип относительности Галилея. Преобразования Галилея.
З-ны
физики не зависят от выбора инерциальн.
системы отсчёта. З-ны ньютона не завис
от инерц со. V-скорость
штриховой со
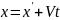 ,
,

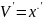 ,
,
 .
В случае, когда инерц. со и тело движ-ся
с малой скоростью, скор-ти склад-ся лин
образом. Преобразования Галилея:
.
В случае, когда инерц. со и тело движ-ся
с малой скоростью, скор-ти склад-ся лин
образом. Преобразования Галилея:
 ,
,
 ,
,
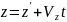 .
Векторная ф-ма:
.
Векторная ф-ма:
 .
С
.
С
 и
и
 тоже самое. Движение одной со относ
другой должн быть равным и прямолин.
2ой з-н Ньютона инвареантен(НЕИЗМЕН
ОТНОСИТ ПРЕОБР ГАЛИЛЕЯ) 3ий относ одной
к другой со.
тоже самое. Движение одной со относ
другой должн быть равным и прямолин.
2ой з-н Ньютона инвареантен(НЕИЗМЕН
ОТНОСИТ ПРЕОБР ГАЛИЛЕЯ) 3ий относ одной
к другой со.
3. Законы Ньютона. Методы решения задач в мех Ньютона.
1ый: Тело неподвижн дейст-ю силБ либо скомпенсир нах в сост покояю 2ой: Ускорение мат (.) прямопропорц силе и обратно пропорц её массе. 3ий: При взаимод 2ух тел. Сила действ одного тела на 2ое =силе противод(по модулю), но противоп по направлению и их действ. реал по прямой соед центры масс этих тел.
4. Теоремы об изменении импульса и момента импульса.
Теорема:
Изменение импульса в единицу
времени=действующ силе на мат (.) в данный
момент.
 .
.
 -кинемат
хар-ка.
-кинемат
хар-ка.
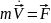 ,
, ,
-диф
форма.
,
-диф
форма.
 интегр форма. Под дейст силы и с временем
интегр форма. Под дейст силы и с временем
 мат (.) преобр импульс
мат (.) преобр импульс
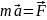 ,
,
 (
( )
Следствие: Если мат (.) не действ никакая
сила, то вып-ся з-н сохр. ипульса
)
Следствие: Если мат (.) не действ никакая
сила, то вып-ся з-н сохр. ипульса
 из котор след
из котор след
 или , если на мат (.) не действ сила, то
она движ равном и прямолин(
или , если на мат (.) не действ сила, то
она движ равном и прямолин( .
Теорема: Изменение момента импульса
в ед времени = моменту силы, действ на
мат (.). Следствие: Если момент силы
.
Теорема: Изменение момента импульса
в ед времени = моменту силы, действ на
мат (.). Следствие: Если момент силы
 ,
то
,
то
 ,
след
,
след
 ,
если на мат (.) нет действия момента
силы,то в этом случ вып-ся закон сохр
момента импульса.
,
если на мат (.) нет действия момента
силы,то в этом случ вып-ся закон сохр
момента импульса.
5.Свойства потенциальных полей
Поле
наз. потенциальным, если для этого
силового поля выполняется соотношение: =-
=-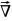 U
U
F-сила,U-потенц. энергия взаимодействия материальной точки с потен. полем.
 ,
, -единицы
вектора
-единицы
вектора
(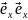 )=1,
(
)=1,
( )=1,
(
)=1,
(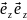 )=1,
(
)=1,
( )=0,
(
)=0,
(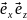 )=0,
(
)=0,
( )=0
)=0
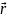 =x
=x +z
+z ;(
;( )=
)= =3
=3
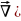 )=
x2+y2+z2)=
)=
x2+y2+z2)=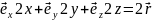
 =
= ,r
= √(x2+y2+z2)
,r
= √(x2+y2+z2)
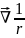 =-
=-

Примеры потенциальных полей
1.Кулоновское
электростатическое поле, т.е.это поле
кот. создается пакоющимися точечными
зарядами.
Из
теории электричества: ,
,
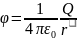 ,
,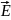 =-
=-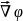
U=q =
= , -
, -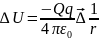 =
=
Вывод: электростатич. кулоновское поле явл. потенциальным.
x2+y2+z2=с2- ур-е сферы.
2.Постоянная гравитационного поля
= , U=
, U=
U= ,R
,R
=m = -
= - ,mg=
,mg=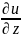 ,
, , U=mgz
, U=mgz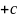 , F= -
, F= -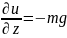
Потенциальная энергия потен. поля опред. С точностью до константы.
U= mgz=const ,z=c’
Вывод: эквипотенциальными плоскостями поля сил тяжести явл.плоскости.
3. Поле упругих сил
F=
-k(x-l) = -kx ,z=x-l ;
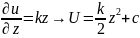 ,
,
 , U=
, U= ,
,
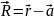
Эквипотенц. поверх-ми поля упругих сил явлю сферы.
