1. Числовые ряды. Сходящиеся ряды. Предел сходящейся последовательности как сумма ряда.

Числовым рядом называется выражение вида где  – действительные или комплексные числа, называемые членами ряда,   - общим членом ряда.

Ряд (1.1) называется сходящимся, если последовательность его частичных сумм (1.5) имеет конечный предел, т.е.

В этом случае число называется суммой ряда (1.1) и пишется

.

Если последовательность имеет предел, то она называется сходящейся к числу A, если нет, то расходящейся. Тот факт, что число A является пределом последовательности {xn}, записывается следующим образом:

.

2. Необходимое условие сходимости числового ряда. Эталонные ряды и их сходимость.

Необходимый признак сходимости ряда

1)Если ряд сходится, то его общий член стремится к нулю при неограниченном возрастании n, т.е.

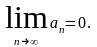
Доказательство теоремы следует из того, что , и если

S – сумма ряда (1.1), то

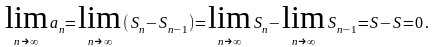
2) Сходящийся ряд можно умножать на число, т.е., если ряд сходится, имеет сумму S и c – некоторое число, тогда

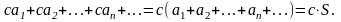
3)Сходящиеся ряды можно почленно складывать и вычитать, т.е. если ряды ,

сходятся,

то и ряд

сходится и его сумма равна т.е.

.

Доказательство следует из свойств предела конечных сумм, т.е.

4) Если у сходящегося ряда   отбросить конечное число первых членов или присоединить в его начале несколько новых членов, это не повлияет на сходимость ряда.

3. Признаки сходимости знакоположительных рядов: признаки сравнения и предельный признак.

Числовой ряд называется знакоположительным, если u_n>0 при всех n=1,2,3… .

Признаки сходимости знакоположительных числовых рядов:

1. Необходимость. Пусть положительный ряд (1) сходится. Это значит, что существует предел 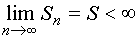 . Кроме того, последовательность частичных сумм {S_n} –  возрастающая, т. к. ряд знакоположительный. Тогда S_n <S, т. е. последовательность {S_n} ограничена и роль числа М выполняет число S.

2. Достаточность. По условию члены последовательности частичных сумм  , т. е. последовательность {S_n} ограничена сверху. К тому же она монотонно возрастает, т. к. ряд — знакоположительный. Поэтому по теореме “ всякая монотонно возрастающая, ограниченная сверху последовательность имеет предел” существует  , то есть ряд (1) сходится.

Теорема 6 (признак сравнения). Если, начиная с некоторого номера (скажем, для n > N), выполняется неравенство  , то из сходимости ряда (2) следует сходимость ряда (1), а из расходимости ряда (1) следует расходимость ряда (2).

Доказательство. Не умаляя общности, положим, что условие   выполняется, начиная с первого номера, т. к. отбрасывание конечного числа членов не влияет на поведение ряда.

Если ряд (2) сходится, то его частичные суммы ограничены по критерию сходимости, значит, частичные суммы ряда (1) и подавно ограничены в силу условия  . Тогда по критерию сходимости ряд (1) сходится.

Пусть теперь ряд (1) расходится. Тогда по критерию сходимости его частичные суммы неограничены, следовательно, частичные суммы ряда (2) (с бoльшими соответствующими членами) тем более неограничены. Поэтому ряд (2) расходится.

Теорема 7 (предельный признак сравнения). Пусть имеем два знакоположительных ряда (1) и (2). Если существует конечный предел  , то ряды (1) и (2) сходятся или расходятся одновременно.

4 билет.

Признаки сходимости знакоположительных рядов: интегральный признак Коши, признак Даламбера., радикальный признак Коши.

Числовой ряд называется знакоположительным, если все его члены положительны, то есть,

Интегральный признак Коши.

Пусть - знакоположительный числовой ряд. Составим функцию непрерывного аргумента y = f(x), аналогичную функции . Пусть функция y = f(x) положительная, непрерывная и убывающая на интервале , где ). Тогда в случае сходимости несобственного интеграла 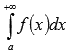сходится исследуемый числовой ряд. Если же несобственный интеграл расходится, то исходный ряд тоже расходится. При проверке убывания функции y = f(x) на интервале .

Признак Даламбера.

Пусть - знакоположительный числовой ряд. Если , то числовой ряд сходится, если , то ряд расходится.

Замечание. Признак Даламбера справедлив, если предел бесконечен, то есть, если , то ряд сходится, если , то ряд расходится.

Если , то признак Даламбера не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.

Радикальный признак Коши.

Пусть - знакоположительный числовой ряд. Если , то числовой ряд сходится, если , то ряд расходится.

Замечание. Радикальный признак Коши справедлив, если предел бесконечен, то есть, если , то ряд сходится, если , то ряд расходится.

Если, то радикальный признак Коши не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.

5 билет.

Знакопеременные ряды. Абсолютная и условная сходимость.

Для знакопеременного ряда существует понятие абсолютной и условной сходимости. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд из абсолютных величин его членов, то есть, сходится знакоположительный числовой ряд .

Знакопеременный ряд называется условно сходящимся, если ряд расходится, а ряд сходится.

6 билет.

Знакочередующиеся ряды. Признак Лейбница.

Числовой ряд называется знакочередующимся, если знаки его соседних членов различны. Знакочередующийся числовой ряд можно записать в виде или , где .