
- •1.Векторная функция скалярного аргумента
- •2. Кривые в пространстве, длина кривой.
- •3.Две леммы о векторной функции скалярного аргумента.
- •4.Сопровождающий трехгранник кривой.
- •5.Соприкасающаяся окружность. Кривизна и кручение кривой.
- •6. Формулы Френе.
- •7. Вычисление кривизны и кручения
- •1. Натуральная параметризация.
- •2. Произвольная параметризация.
- •Касательная плоскость и нормаль к поверхности
- •Уравнение касательной плоскости имеет вид
- •9. Первая квадратичная форма поверхности
- •Площадь поверхности.
- •10.Криволинейные системы координат.
- •2) Сферическая система координат.
- •11.Дифференцирование скалярного поля.
- •12.Дифференцирование векторного поля.
- •13)Оператор Гамильтона. Дифференцирование произведений.
- •14.Дифференциальные операции второго порядка над полями.
- •15)Поверхностный интеграл первого рода.
- •21.Инвариантное определение операций div, grad, rot…
- •28.Ряды Фурье по общим ортогональным системам.
- •30.Замкнутость и полнота ортогональных систем функций. Замкнутость тригонометрической системы.
- •32.Интегральная формула Фурье.
21.Инвариантное определение операций div, grad, rot…






22.Потенциальные векторные поля.
Векторное поле a называется потенциальным в области G, если циркуляция этого поля по любому замкнутому кусочно гладкому контуру, расположенному в области G равна нулю.
Трехмерная область G ⊂ E3 называется поверхностно односвязной, если для любого замкнутого кусочно гладкого контура γ ∈ G можно указать такую ориентируемую кусочно гладкую поверхность Ω ∈ G, границей которой является контур γ.


представляет собой функцию точки M.
Докажем что в каждой точке M существуют
частные производные этой функции,
причем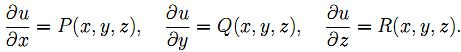 Для
этого рассмотрим точку N(x + ∆x, y, z), не
выходящую за пределы области. тогда
Для
этого рассмотрим точку N(x + ∆x, y, z), не
выходящую за пределы области. тогда
 На
отрезке MN величины y и z постоянны,
следовательно
На
отрезке MN величины y и z постоянны,
следовательно
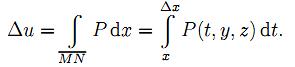 Применяя
к интегралу теорему о среднем,
получим
Применяя
к интегралу теорему о среднем,
получим![]() Откуда
в силу непрерывности функции P(x, y, z)
получаем
Откуда
в силу непрерывности функции P(x, y, z)
получаем
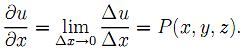



23.Соленоидальные векторные поля.



24.Ортогональные
криволинейные системы координат.
Градиент в криволинейных координатах.

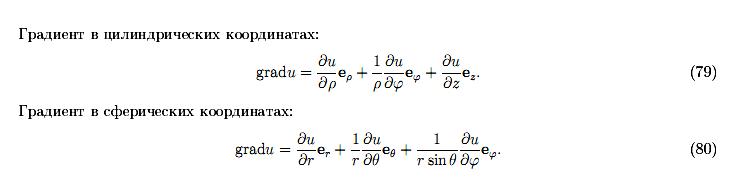
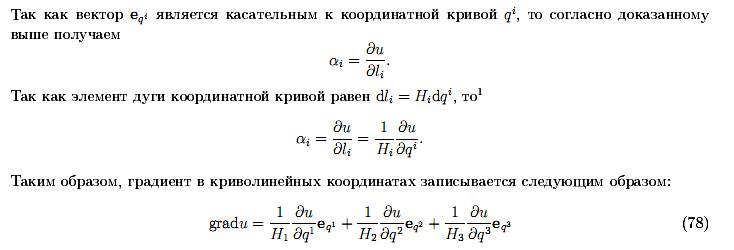
25.Дивергенция, ротор и оператор Лапласа в криволинейных координатах.





26.Тригонометрические ряды Фурье.
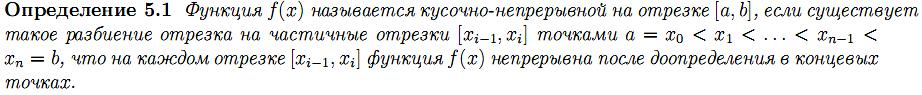



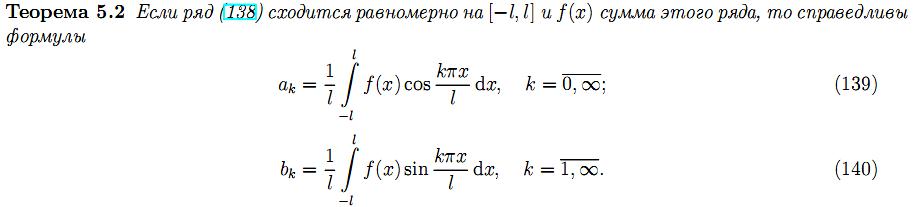
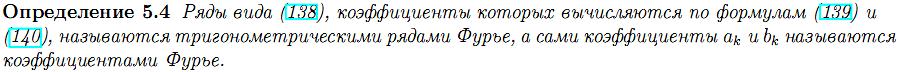
27.Сходимость тригонометрического ряда Фурье.
ряд Фурье
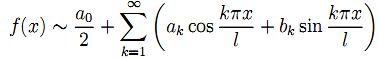

![]()
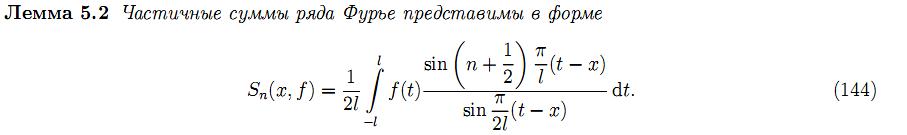
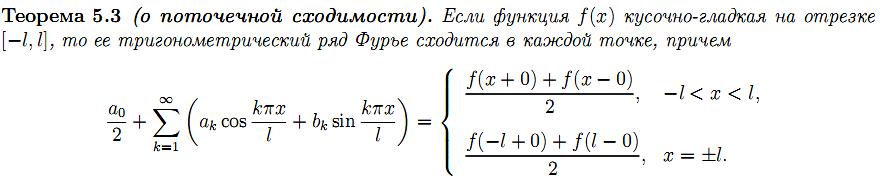

28.Ряды Фурье по общим ортогональным системам.
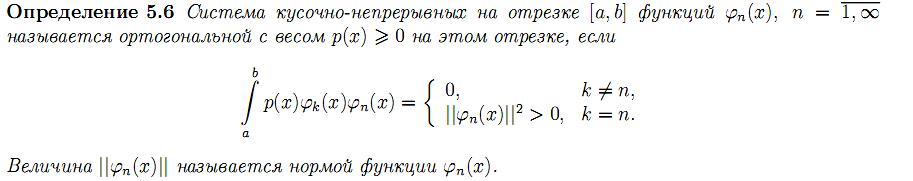
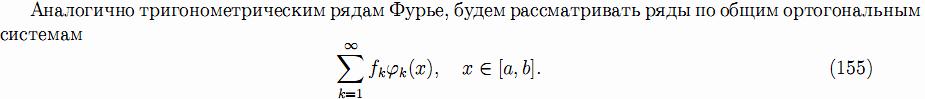

Ряды вида (155), коэффициенты которых вычисляются по формуле (156),называются рядами Фурье по общим ортогональным системам, а сами коэффициенты fk называются коэффициентами Фурье.
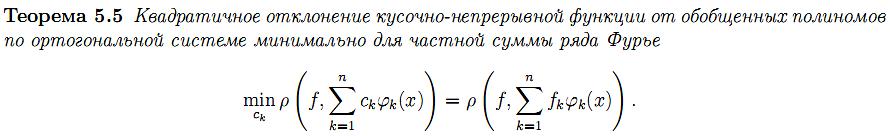
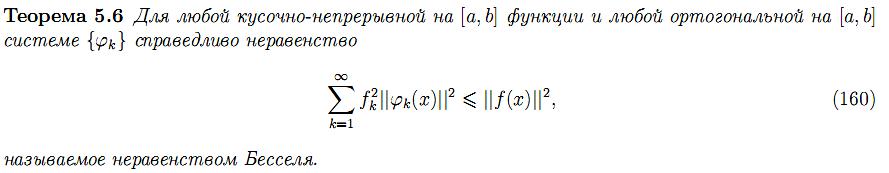

29.Равномерная
сходимость ряда Фурье.

30.Замкнутость и полнота ортогональных систем функций. Замкнутость тригонометрической системы.
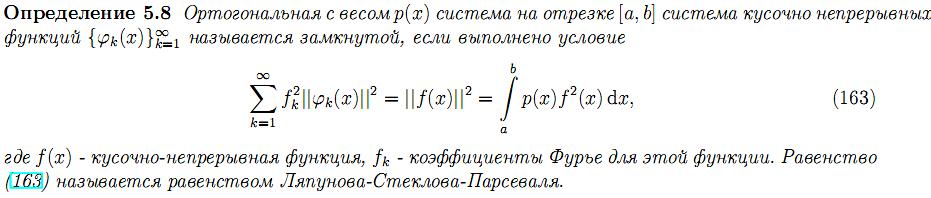


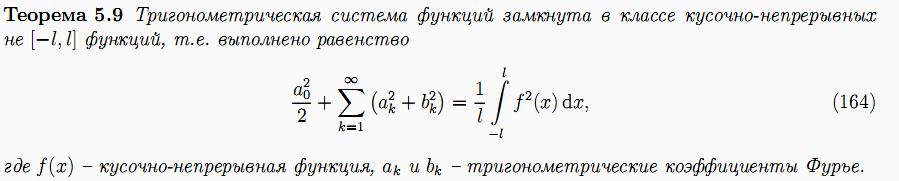
31.Комплексные
и многомерные ряды Фурье


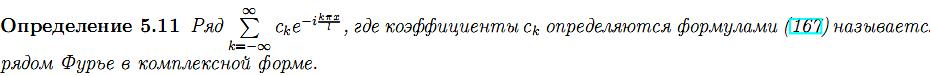

32.Интегральная формула Фурье.
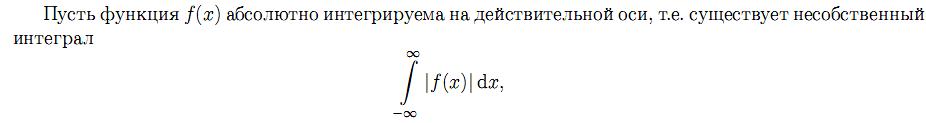
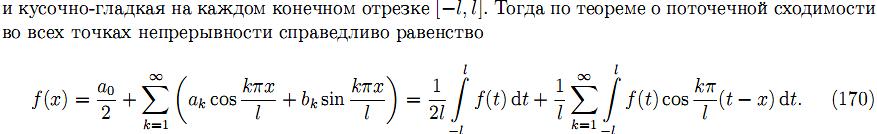

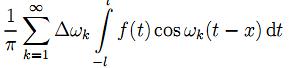 для
интеграла
для
интеграла
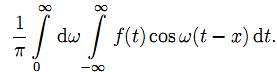
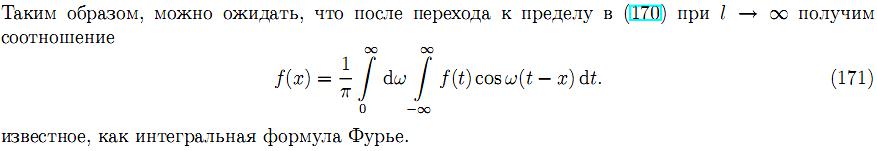
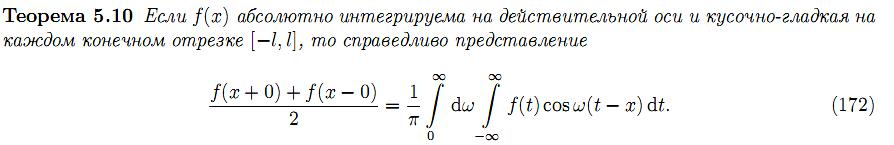
33. Преобразование Фурье



