1.Векторная функция скалярного аргумента

Векторные функции скалярного аргумента. Предел, непрерывность, производная и интеграл Римана вектор-функции.

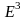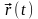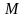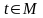Будем рассматривать трёхмерное Евклидово пространство , т.е. пространство, в котором определена операция скалярного произведения. Говорят, что в задана векторная функция , определённая на множестве , если для каждого ставится в соответствие 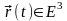(причём - одномерное множество).

Рассмотрим случай, когда 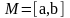-отрезок. В введём ортонормированный базис 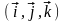. Тогда вектор можно разложить по данному базису: 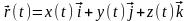, где , , 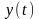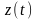- проекции вектора на соответствующие орты. 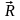назовем пределом векторной функции в точке , если 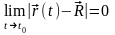(1). Так как под знаком предела стоит модуль, то это скалярная величина. Обозначим этот предел как 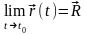. (но подразумевать под этим выражением будем выражение (1)). Если 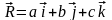, то можно доказать следующее утверждение:

Теорема 1: является пределом функции в точке тогда и только тогда , когда , , 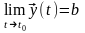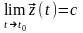. Доказательство.

Непосредственно из опр. имеем: 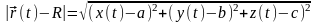. Очевидно, что правая часть равенства (2) стремиться к 0, так как , , 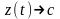при 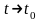. Так как каждая из скобок стремиться к 0, то и левая часть равенства (1) стремиться к 0, что и требовалось доказать.

В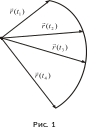 екторная функция называется непрерывной в точке , если .

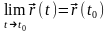Векторная функция называется непрерывной на отрезке 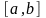, если она непрерывна в каждой точке отрезка.

Из непрерывности функции следует непрерывность её компонентов , , и наоборот.

Производной векторной функции в точке t называется:

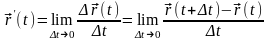. Производная обозначается несколькими эквивалентными способами: 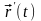, 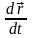. Вторая производная определяется как производная от первой .

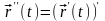Выберем точку и отложим от неё множество векторов (см. рис. 1). Кривая, которую образуют концы векторов, называется годографом.

Р ассмотрим более подробно два соседних вектора и их разность (см. рис. 2). Очевидно, что вектор 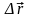при 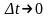начинает скользить по годографу. То есть геометрическим смыслом производной является вектор, лежащий на касательной к годографу.

Для того, что бы функция была дифференцируема, необходимо выполнение равенства : ,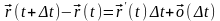

где .

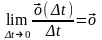Свойства производной.

1. .

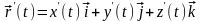2. .

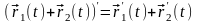3. .

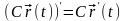4. .

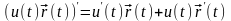5. .

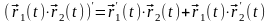6. .

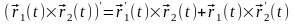Теорема 2: Если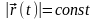 , то вектор перпендикулярен вектору .

Доказательство. Из условия теоремы имеем: 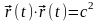. Продифференцировав это равенство, получим: 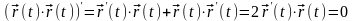, что и требовалось доказать.

Используя равенство 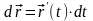, можно разложить векторную функцию в ряд Тейлора:

.

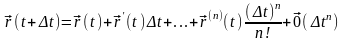2. Кривые в пространстве, длина кривой.

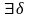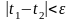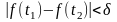
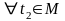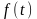Понятие прямая так же как и понятие точки первичны и не определяются. Рассмотрим отображение некоторой точки в трехмерное пространство и обозначим его . Будем говорить, что отображение непрерывно, если , такое, что если , то . Если отображение непрерывно в каждой точке М, то оно непрерывно и на всём множестве М.

Непрерывное отображение отрезка в пространстве называется линией в пространстве. Также под линией будем понимать образ, полученный при таком отображении. Линии в пространстве удобно описывать в виде 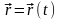, причём если эти векторы откладывать от одной точки.

Рассмотрим случай, когда образы двух векторных функций совпадают, то есть , 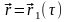, где 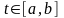, . Эти две линии определяют одну линию, если существует монотонная функция 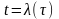, , 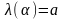, 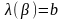такая что .

Линию 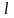назовем гладкой, если векторная функция (где ), определяющая эту линию, имеет непрерывную производную во всех точках отрезка .

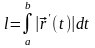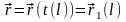Всякая гадкая линия, заданная уравнением (где ), имеет конечную дину, которая может быть вычислена по следующей формуле: . Когда в качестве параметра выбрана длина линии ,то говорят, что линия задана в натуральной параметризации, а сам параметр l называется натуральным параметром.

Линия L, заданная уравнением , называется кусочно-гладкой, если отрезок можно разделить на конечное множество отрезков, на каждом из которых линия будет гладкой.

Кривая L называется спрямляемой, если множество длин всевозможных ломанных, вписанных в кривую указанным выше образом, ограничено. Точная верхняя грань этого множества называется длиной дуги кривой.

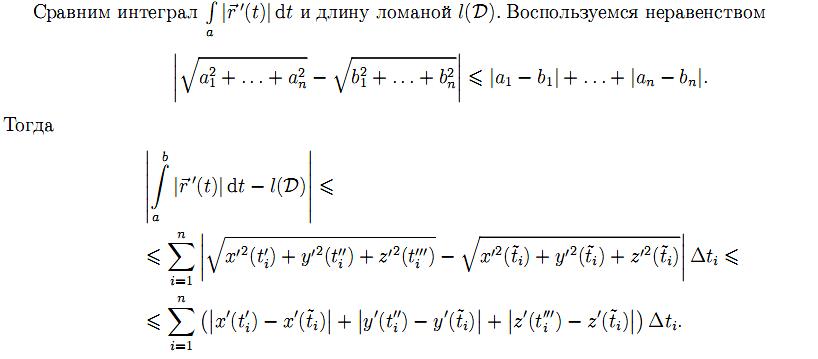
Свойства длины дуги кривой:

1◦. Если кривая L1 является частью спрямляемой кривой L, то кривая L1 также спрямляема.

2◦Если кривая L разбита точкой N на две спрямляемые части L1 и L2, то кривая L спрямляема и для длин дуг кривых L1, L2 и L справедливо соотношение L1 + L2 = L

3◦ Обозначим через l(t) длину дуги кривой L соответствующей значениям параметра из отрезка[a, t]. Функция l(t) строго монотонна и непрерывна на отрезке [a, b] и положительна при t > a. Если выполнены условия теоремы 1.4, то функция l(t) имеет вид

Пусть r’ (t) != 0. Тогда существует функция t = t(l), обратная к функции l = l(t) и дифференци-

руема столько раз, сколько и функция r(t).Функция l(t) называется натуральным параметром кривой.