
- •1 Билет
- •2 Билет Определители n-го порядка.
- •3 Билет
- •Алгоритм нахождения обратной матрицы
- •Решение матричных уравнений
- •4 Билет
- •4.1. Основные понятия
- •Решение системы по формулам Крамера
- •5 Билет
- •Достоинства метода
- •6 Билет
- •Определение
- •7 Билет Вектором называется величина, характеризующаяся не только численным значением, но и направлением в пространстве.
- •Базис системы векторов
- •Алгоритм нахождения базиса системы векторов
- •8 Билет Деление отрезка в данном отношении
- •9 Билет
- •Геометрические свойства векторного произведения
- •10 Билет
- •Прямая на плоскости
- •11 Билет
- •12 Билет
- •13 Билет
- •14 Билет
- •15 Билет
- •Бесконечно малая величина
- •]Пример
- •16 Билет
- •Сравнение бесконечно малых
- •17 Билет
- •Свойства функций, непрерывных на отрезке
- •18 Билет
- •1.3 Общее правило нахождения производной
- •1.4 Геометрический смысл производной
- •1.5 Механический смысл производной
- •Правила дифференцирования
12 Билет
Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
![]()
в
котором по крайней мере один из
коэффициентов ![]() отличен
от нуля.
отличен
от нуля.
Если кривая Г невырожденная, то для неё найдется такая декартова прямоугольная система координат, в которой уравнение этой кривой примет один из следующих трех видов (каноническое уравнение):
![]() -
эллипс,
-
эллипс,
![]() -
гипербола,
-
гипербола,
![]() px -
парабола.
px -
парабола.
Эллипс –
геометрическое множество точек плоскости,
сумма расстояний от которых до двух
точек ![]() и
и ![]() ,
называемых фокусами, есть величина
постоянная 2a,
большая, чем расстояние между фокусами
2c:
,
называемых фокусами, есть величина
постоянная 2a,
большая, чем расстояние между фокусами
2c: ![]() .
Эллипс,
заданный каноническим уравнением:
.
Эллипс,
заданный каноническим уравнением: 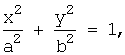
симметричен относительно
осей координат. Параметры а и b называются
полуосями эллипса (большой и малой
соответственно), точки ![]() ,
, ![]() ,
, ![]() ,
, ![]() называются
его вершинами.
называются
его вершинами.
Гипербола – геометрическое
множество точек плоскости, модуль
разности расстояний от которых до двух
точек ![]() и
и ![]() ,
называемых фокусами, есть величина
постоянная 2a,
меньшая, чем расстояние между фокусами
2c:
,
называемых фокусами, есть величина
постоянная 2a,
меньшая, чем расстояние между фокусами
2c: ![]() .
.
Гипербола, заданная каноническим уравнением:
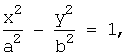
симметрична относительно
осей координат. Она пересекает ось ОХ
в точках ![]() и
и ![]() -
вершинах гиперболы, и не пересекает оси
ОY.
-
вершинах гиперболы, и не пересекает оси
ОY.
Парабола – множество точек плоскости, равноудаленных от данной точки F, называемой
фокусом,
и данной прямой, называемой директрисой: ![]() .
.
Парабола, заданная указанным каноническим уравнением, симметрична относительно оси ОХ.
Уравнение ![]() задает
параболу, симметричную относительно
оси ОY.
задает
параболу, симметричную относительно
оси ОY.
Парабола ![]() имеет
фокус
имеет
фокус ![]() и
директрису
и
директрису ![]() .
.
Парабола
имеет
фокус ![]() и
директрису
и
директрису ![]() .
.
13 Билет
Поверхность и ее уравнение
Поверхность в пространстве можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в точке О1 есть геометрическое место всех точек пространства, находящихся от точки O1 на расстоянии R. Прямоугольная система координат Oxyz в пространстве позволяет установить взаимно однозначное соответствие между точками пространства и тройками чисел х, у и z — их координатами. Свойство, общее всем точкам поверхности, можно записать в виде уравнения, связывающего координаты всех точек поверхности. Уравнением данной поверхности в прямоугольной системе координат Oxyz называется такое уравнение F(x, у, z) = 0 с тремя переменными х, у и z, которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности. Переменные х, у и z в уравнении поверхности называются текущими координатами точек поверхности.
Плоскость в пространстве.
Получим сначала уравнение плоскости, проходящей через точку М0(х0 ,у0 ,z0) перпендикулярно вектору n = {A,B,C},называемому нормалью к плоскости. Для любой точки плоскости М(х, у, z) вектор М0М = {x - x0 , y - y0 , z - z0) ортогонален вектору n, следовательно, их скалярное произведение равно нулю:
A(x - x0) + B(y - y0) + C(z - z0) = 0. (8.1)
Получено уравнение, которому удовлетворяет любая точка заданной плоскости – уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.
После приведения подобных можно записать уравнение (8.1) в виде:
Ax + By + Cz + D = 0, (8.2)
где D = -Ax0 - By0 - Cz0. Это линейное уравнение относительно трех переменных называют общим уравнением плоскости.
Уравнения линии в пространстве
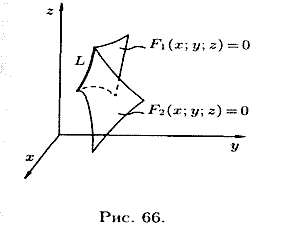
Линию в пространстве можно рассматривать как линию пересечения двух поверхностей (см. рис. 66) или как геометрическое место точек, общих двум поверхностям.
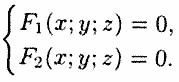 (12.1)
Сравнения системы (12.1) называются
уравнениями линии в пространстве.
Например,
(12.1)
Сравнения системы (12.1) называются
уравнениями линии в пространстве.
Например,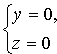 есть
уравнения оси Ох.
есть
уравнения оси Ох.
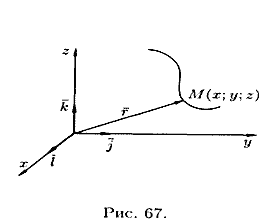
Линию в пространстве можно рассматривать как траекторию движения точки (см. рис. 67). В этом случае ее задают векторным уравнением
![]()
![]() (12.2)
(12.2)
или параметрическими уравнениями
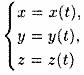 проекций
вектора (12.2) на оси координат.
проекций
вектора (12.2) на оси координат.
Н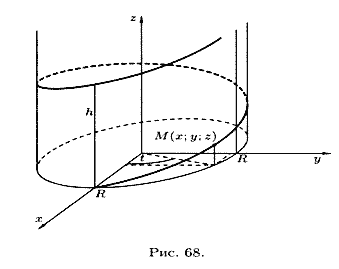 апример,
параметрические уравнения винтовой
линии имеют вид
апример,
параметрические уравнения винтовой
линии имеют вид
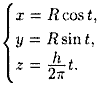
Если точка Μ равномерно движется по образующей кругового цилиндра, а сам цилиндр равномерно вращается вокруг оси, то точка Μ описывает винтовую линию (см. рис. 68).
Простейшей поверхностью является плоскость. Плоскость в пространстве Oxyz можно задать разными способами. Каждому из них соответствует определенный вид ее уравнения.
Уравнение
плоскости, проходящей через данную
точку перпендикулярно данному вектору
Пусть в пространстве
Oxyz плоскость Q задана точкой ![]() и
вектором
и
вектором ![]() ,
перпендикулярным этой плоскости (см.
рис. 69). Выведем уравнение плоскости Q.
Возьмем на ней произвольную точку
,
перпендикулярным этой плоскости (см.
рис. 69). Выведем уравнение плоскости Q.
Возьмем на ней произвольную точку ![]() и
составим вектор
и
составим вектор ![]() .
При любом
расположении точки Μ на плоскости Q
векторы
.
При любом
расположении точки Μ на плоскости Q
векторы ![]() и
и ![]() взаимно
перпендикулярны, поэтому их скалярное
произведение равно нулю:
взаимно
перпендикулярны, поэтому их скалярное
произведение равно нулю: ![]() ,
т. е.
,
т. е.
![]()
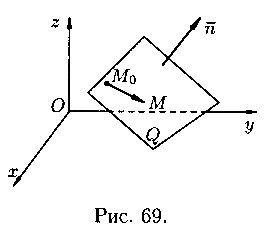 (12.3)
(12.3)
Координаты
любой точки плоскости Q удовлетворяют
уравнению (12.3), координаты точек, не
лежащих на плоскости Q, этому уравнению
не удовлетворяют (для них ![]() ).
).
Уравнение (12.3) называется уравнением плоскости, проходящей через данную точку перпендикулярно вектору . Оно первой степени относительно текущих координат x, y, z. Вектор называется нормальным вектором плоскости.
Придавая
коэффициентам А, В и С уравнения (12.3)
различные значения, можно получить
уравнение любой плоскости, проходящей
череp точку ![]() .
Совокупность плоскостей, проходящих
через данную точку, называется связкой
плоскостей, а уравнение (12.3) - уравнением
связки плоскостей.
.
Совокупность плоскостей, проходящих
через данную точку, называется связкой
плоскостей, а уравнение (12.3) - уравнением
связки плоскостей.
