Решение системы по формулам Крамера

Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!

Рассмотрим систему уравнений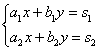 

На первом шаге вычислим определитель 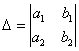  , его называют главным определителем системы. Если  , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать Метод Гауса.

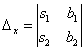Если  , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:  и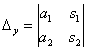 

На практике вышеуказанные определители также могут обозначаться латинской буквой  .

Корни уравнения находим по формулам: , 

Пример 7

Решить систему линейных уравнений 

В подобных случаях и приходят на помощь формулы Крамера.

, значит, система имеет единственное решение.

;

; 

Ответ:  ,  .

Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения     в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.

Пример 8 Решить систему по формулам Крамера.  Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

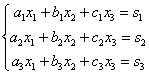
Находим главный определитель системы:

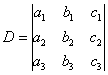
Если  , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.

Если  , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя: ,  , 

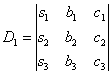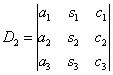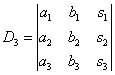
И, наконец, ответ рассчитывается по формулам: ,  , 

Пример 9 Решить систему по формулам Крамера.  

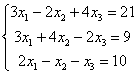
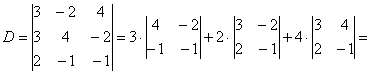
Решение: Решим систему по формулам Крамера. , значит, система имеет единственное решение.

Ответ:  .

5 Билет

Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.

Элементарными преобразованиями строк называют:

• перестановка местами любых двух строк матрицы;

• умножение любой строки матрицы на константу  ,  ;

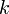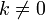• прибавление к любой строке матрицы другой строки, умноженной на константу  ,  .

В некоторых курсах линейной алгебры перестановка местами двух строк матрицы не вносятся в определение элементарных преобразований так как перестановку местами любых двух строк матрицы можно получить используя умножение любой строки матрицы на константу  ,   и прибавление к любой строке матрицы другой строки, умноженной на константу  ,  .

Аналогично определяются элементарные преобразования столбцов.

Элементарные преобразования обратимы.

Обозначение   указывает на то, что матрица   может быть получена из   путём элементарных преобразований (или наоборот).

Ме́тод Га́усса^[1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные^[2].

Решить систему уравнений методом Гаусса:

                                                      x +  y - 3z = 2,

                                                    3x - 2y +  z = - 1,

                                                    2x +  y - 2z = 0.

Решение. Выпишем расширенную матрицу данной системы

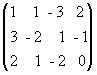
и произведем следующие элементарные преобразования над ее строками:

а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:

 ~  ;

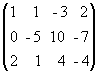б) третью строку умножим на (-5) и прибавим к ней вторую:

.

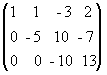В результате всех этих преобразований данная система приводится к треугольному виду:

                                                    x + y - 3z = 2,

                                                    -5y + 10z = -7,

                                                           - 10z = 13.

Из последнего уравнения находим z = -1,3. Подставляя это значение во второе уравнение, имеем y = -1,2. Далее из первого уравнения получим  x = - 0,7.