
- •1 Билет
- •2 Билет Определители n-го порядка.
- •3 Билет
- •Алгоритм нахождения обратной матрицы
- •Решение матричных уравнений
- •4 Билет
- •4.1. Основные понятия
- •Решение системы по формулам Крамера
- •5 Билет
- •Достоинства метода
- •6 Билет
- •Определение
- •7 Билет Вектором называется величина, характеризующаяся не только численным значением, но и направлением в пространстве.
- •Базис системы векторов
- •Алгоритм нахождения базиса системы векторов
- •8 Билет Деление отрезка в данном отношении
- •9 Билет
- •Геометрические свойства векторного произведения
- •10 Билет
- •Прямая на плоскости
- •11 Билет
- •12 Билет
- •13 Билет
- •14 Билет
- •15 Билет
- •Бесконечно малая величина
- •]Пример
- •16 Билет
- •Сравнение бесконечно малых
- •17 Билет
- •Свойства функций, непрерывных на отрезке
- •18 Билет
- •1.3 Общее правило нахождения производной
- •1.4 Геометрический смысл производной
- •1.5 Механический смысл производной
- •Правила дифференцирования
8 Билет Деление отрезка в данном отношении
Если
точка М(x; y) лежит на
прямой, проходящей через две данные
точки ![]() (
(![]() ,
, ![]() )
и
)
и ![]() (
(![]() ,
, ![]() ),
и дано отношение
),
и дано отношение ![]() ,
в котором точка М делит отрезок
,
в котором точка М делит отрезок ![]() ,
то координаты точки М определяются по
формулам
,
то координаты точки М определяются по
формулам
![]() ,
, ![]() .
.
Если точка М является серединой отрезка , то ее координаты определяются по формулам
![]() ,
, ![]() .
.
Скалярным
произведением
векторов ![]() и
и ![]() ,
называется число, численно равное
произведению длин векторов на косинус
угла между ними.
,
называется число, численно равное
произведению длин векторов на косинус
угла между ними.
 *
=|
*
|*cos(
-
)
*
=|
*
|*cos(
-
)
* =x1y1+x2y2+…+xnyn
Свойства скалярного произведения.
Симметричность :
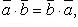

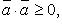
* =>| |=0
* =| |2
4)
![]()
9 Билет
Векторное произведение — это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции«векторное умножение» над векторами в трёхмерном Евклидовом пространстве.
Векторным
произведением вектора ![]() на
вектор
на
вектор ![]() называется
вектор
называется
вектор ![]() ,
удовлетворяющий следующим требованиям:
,
удовлетворяющий следующим требованиям:
длина вектора равна произведению длин векторов и на синус угла
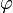 ;
между ними
;
между ними
![]()
вектор ортогонален каждому из векторов и
вектор направлен так, что тройка векторов
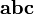 является
правой.
является
правой.в случае пространства
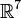 требуется
ассоциативность тройки векторов
требуется
ассоциативность тройки векторов 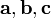 .
.
Обозначение:
![]()
Геометрические свойства векторного произведения
П
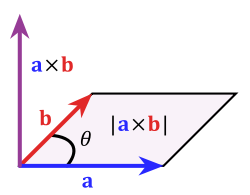 лощадь
параллелограмма равна векторному
произведению.
лощадь
параллелограмма равна векторному
произведению.
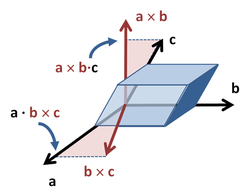
Объём
параллелепипеда при использовании
векторного и скалярного произведения
векторов; пунктирные линии показывают
проекции вектора c на a
× b и
вектора a на b
× c,
первым шагом является нахождение
скалярных произведений.
Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.
Модуль векторного произведения
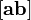 равняется
площади S параллелограмма,
построенного на приведённых к общему
началу векторах
и
(см.
Рисунок 1)
равняется
площади S параллелограмма,
построенного на приведённых к общему
началу векторах
и
(см.
Рисунок 1)Если
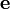 — единичный
вектор,
ортогональный векторам
и
и
выбранный так, что тройка
— единичный
вектор,
ортогональный векторам
и
и
выбранный так, что тройка 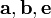 —
правая, а S —
площадь параллелограмма, построенного
на них (приведённых к общему началу),
то для векторного произведения
справедлива формула:
—
правая, а S —
площадь параллелограмма, построенного
на них (приведённых к общему началу),
то для векторного произведения
справедлива формула:
![]()
При использовании векторного и скалярного произведений можно высчитать объём параллелепипеда, построенного на приведённых к общему началу векторах a, b и c. Такое произведение трех векторов называется смешанным.
![]()
На рисунке показано, что этот объём может быть найден двумя способами: геометрический результат сохраняется даже при замене «скалярного» и «векторного» произведений местами:
![]()
Величина векторного произведения зависит от синуса угла между изначальными векторами, поэтому векторное произведение может восприниматься как степень «перпендикулярности» векторов также, как и скалярное произведение может рассматриваться как степень «параллельности». Векторное произведение двухединичных векторов равно 1 (единичному вектору), если изначальные векторы перпендикулярны, и равно 0, если векторы параллельны.
Смешанным
произведением трёх
векторов
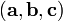 ,
называется такое число, равное скалярному
произведению первого из них на векторное
произведение двух других.
,
называется такое число, равное скалярному
произведению первого из них на векторное
произведение двух других.
![]() .
.
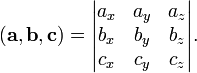
Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр(точнее — псевдоскаляр).
Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами .
