9.6. Політропні процеси

Дотепер розглядалися процеси, в яких були цілком визначені ознаки: ізохорний процес здійснювався при постійному об'ємі; ізобарний - при постійному тиску; ізотермічний - при постійній температурі; адіабатний - при відсутності теплообміну між робочим тілом і зовнішнім середовищем. Поряд із цими процесами можна представити ще нескінченну множину процесів, у яких є інші постійні ознаки.

Умовилися всякий процес ідеального газу, у якому теплоємність є постійною величиною, називати політропним процесом, а лінію процесу — політропою.

З визначення політропного процесу слідує, що основні термодинамічні процеси - ізохорний, ізобарний, ізотермічний і адіабатний, якщо вони протікають при постійній теплоємності, є окремими випадками політропного процесу.

Теплоємність політропного процесу с_п може приймати найрізноманітніші позитивні й негативні значення від + ∞ до - ∞.

Кількість теплоти, що бере участь у політропному процесі, може бути виражено добутком теплоємності процесу с_п на різницю температур Т₂ — Т₁ у кінцевому й початковому станах:

^{( 7-19)}

Рівняння політропного процесу виводиться на підставі рівняння першого закону термодинаміки:

Із цих рівнянь знайдемо

Позначивши вираження лівої частини рівняння через п, отримаємо

Інтегруючи отримане співвідношення в межах від початку до кінця процесу, знаходимо ,

або

pvⁿ = const. ( 7-20)

Отримане рівняння є рівнянням політропного процесу.

Показник політропи п приймає для кожного процесу певне числове значення. Для основних процесів: ізохорних п = ± ∞, ізобарних п = 0, ізотермічних п = 1 і адіабатних п = k.

Оскільки рівняння політропи відрізняється від рівняння адіабати тільки величиною показника п, то, очевидно, всі співвідношення між основними параметрами можуть бути представлені формулами, аналогічними адіабатному процесу:

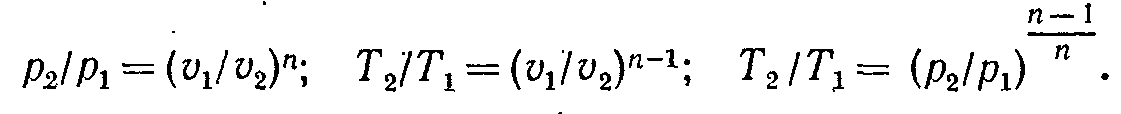
Теплоємність політропного процесу визначаємо із формули

^{( 7-21)}

Рівняння ( 7-21) дозволяє визначити теплоємність політропного процесу для кожного значення п.

Якщо в рівняння ( 7-21) підставити значення п для окремих випадків, то отримуємо теплоємності розглянутих процесів:

ізохорного процесу n = ± ∞, с_n = с_v;

ізобарного процесу п = 0, c_n = kс_v = c_р;

ізотермічного процесу п = 1, с_n = ± ∞;

адіабатного процесу п = k, с_n = 0.

Рівняння роботи зміни об'єму, чиненої тілом при політропному процесі, має аналогічний вигляд з рівнянням роботи в адіабатному процесі, тобто

^{( 7-22)}

або

^{( 7-23)}

Зміна внутрішньої енергії газу й теплота в політропному процесі визначаються по формулах:

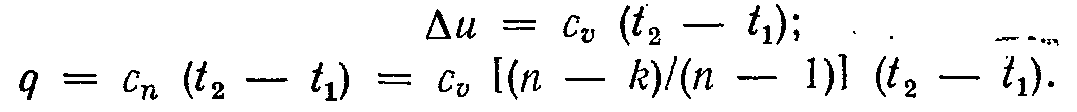( 7-24)

Розташовувана зовнішня робота в політропному процесі за аналогією з адіабатним процесом дорівнює

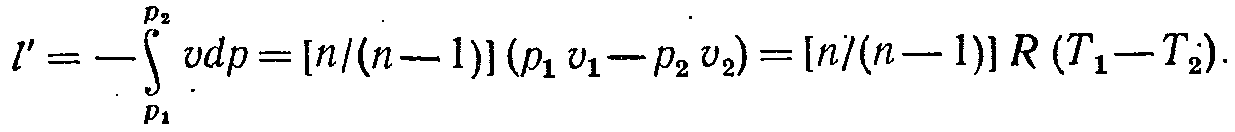( 7-25)

Зміна ентальпії в політропному процесі

^{( 7-26)}

Значення n у будь-якому політропному процесі може бути визначене по координатах двох будь-яких точок графіка:

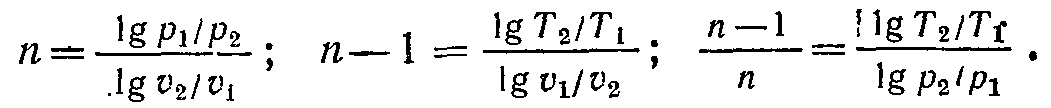( 7-27)

Логарифмуючи рівняння політропи, отримаємо

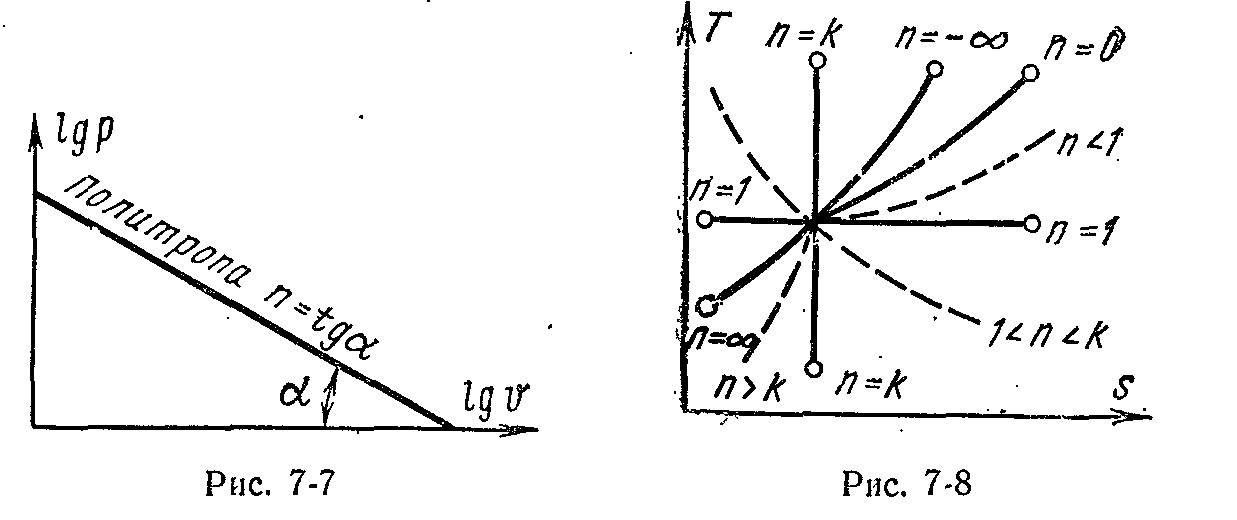
lg р + n lg v = const.

Це рівняння являє собою рівняння прямої лінії в координатах lg р і lg v, а показник політропи n — тангенс кута нахилу прямій до осі абсцис (мал. 7-7).

Зміна ентропії газу в політропному процесі визначається по формулі

ds = dq/T = c_n d/T,

або для кінцевої зміни стану

( 7-28)