3. Точечные оценки неизвестных параметров. Несмещенные, состоятельные, эмпирические оценки.

Предположим, что имеется выборка из генеральной совокупности, закон распределения которой зависит от неизвестного параметра (например, функция распределения ).

О1. Оценкой или статистикой параметра называется любая функция от выборочных значений .

О2. Оценка неизвестного параметра называется несмещенной, если математическое ожидание .

О3. Оценка неизвестного параметра называется состоятельной, если сходится по вероятности k a ( т.е. для ) .

О4. Несмещенная оценка неизвестного параметра называется эффективной, если она имеет наименьшую дисперсию среди всех несмещенных оценок параметра .

┐ несмещенная оценка параметра , тогда эффективна, если

Пример: Предположим, что имеется выборка из генеральной совокупности с , . Здесь - генеральная средняя, - генеральная дисперсия.

В качестве оценки возьмем выборочную среднюю . В качестве оценки возьмем выборочную дисперсию . Проверим, насколько хороша оценка :

1. Вывод: - несмещенная оценка параметра .

4. Методы получения оценок. Метод моментов.

Пусть - выборка из генеральной совокупности с функцией распределения , зависящей от неизвестных параметров. Необходимо найти оценки параметров . при больших . Более того, можно рассматривать как оценку или при каждом фиксированном значении . Поскольку - результаты n испытаний для случайной величины , то в качестве успеха в случайном испытании примем: .

Тогда , где - число выборочных значений, меньших , т.е. число успехов. , где ,

. Таким образом, . Следовательно,

1.

При любом фиксированном является несмещенной оценкой .

2. Проверим состоятельность оценки

т.к. ,

5. Методы получения оценок. Метод максимального правдоподобия.

Пусть - выборка из генеральной совокупности с функцией распределения , зависящей от неизвестных параметров. Необходимо найти оценки параметров . при больших . Более того, можно рассматривать как оценку или при каждом фиксированном значении . Поскольку - результаты n испытаний для случайной величины , то в качестве успеха в случайном испытании примем: .

Тогда , где - число выборочных значений, меньших , т.е. число успехов. , где ,

. Таким образом, . Следовательно,

1.

При любом фиксированном является несмещенной оценкой .

2. Проверим состоятельность оценки

т.к. , если - конечно. По теореме о двух милиционерах .

Т.о. , т.е. - состоятельная оценка .

3. Оказывается, что эта оценка является также и эффективной.

Метод максимального правдоподобия.

Пусть выборка из генеральной совокупности, имеющей плотность , зависящую от . Составим совместную плотность распределения случайных величин .

(по критерию независимости непрерывных случайных величин)= . - функция правдоподобия.

Фишер предложил находить оценки из того условия, что функция правдоподобия .

Те значения , при которых функция принимает наибольшее значение, и являются оценками.

Введем функцию - логарифмическую функцию правдоподобия. Надо решать задачу .

Для этого составляется система

Выбирается то решение, которое обращает функцию правдоподобия (следовательно и ) в максимум. При этом методе получаются состоятельные ,но смещенные оценки.

О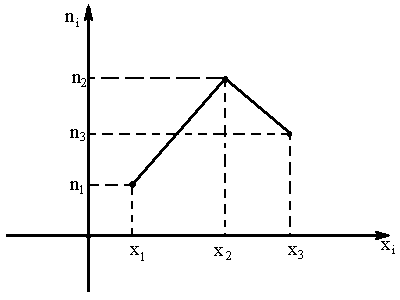 .Полигоном частот называют ломаную, отрезки которой соединяют точки Для построения полигона частот на оси абсцисс откладывают варианты , а на оси ординат – соответствующие им частоты . Точки соединяют отрезками и получают полигон частот.

О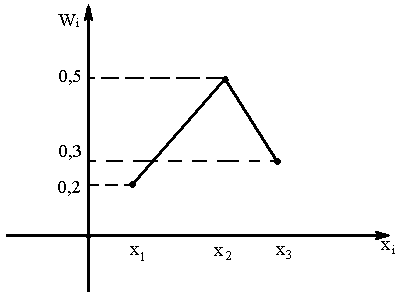 . Полигоном относительных частот называют ломаную, отрезки которой соединяют точки

Предположим, что - выборка из непрерывной генеральной совокупности с плотностью вероятности . Необходимо построить оценку плотности .

Интервал, в котором заключены все наблюдаемые значения, разбиваем на k частичных интервалов длины

, где - наибольшая, а - наименьшая из вариант,

, где - число выборочных значений, попадающих в i – й интервал , n – объем выборки.

Полученная ступенчатая фигура называется гистограммой относительных частот.

О.Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной , а высоты равны отношению (вместо )

Площадь , т.е. равна сумме всех частот, т.е. объему выборки.

2. Поскольку - независимы, . По закону больших чисел в форме Чебышева По определению 3 - состоятельная оценка параметра .

3. Эффективность оценки зависит от закона распределения генеральной совокупности.

Оценка .

1. .Следовательно, (1)

.

Следовательно, (2)

Следовательно, не является несмещенной оценкой. При оценка будет почти несмещенной.

2. Можно проверить, что - состоятельная. Введем , тогда

- несмещенная оценка и называется исправленной выборочной дисперсией.

- неисправленная выборочная дисперсия.

- исправленная выборочная дисперсия.

если - конечно. По теореме о двух милиционерах .

Т.о. , т.е. - состоятельная оценка .

3. Оказывается, что эта оценка является также и эффективной.

Метод моментов.

Состоит в том, что выборочные (эмпирические) моменты принимаются за оценки соответствующих теоретических (генеральных) моментов и неизвестные параметры выражаются через эти моменты.

Начальные моменты:

1. Теоретические (генеральные)

где - вероятность - плотность случайной величины X.

2. выборочные (эмпирические) .

Центральные моменты:

1. Теоретические (генеральные)

2. выборочные (эмпирические) .

Необходимо отметить, что теоретическая моменты – случайные величины, а эмпирические – фиксированные постоянные.

Т аким образом, для получения оценок неизвестных параметров необходимо решить одну из систем уравнений:

Здесь оценки параметров заменены на сами параметры.