
- •22. Дисперсионный анализ.
- •24. Методы расчета сводных характеристик выборки. Условные варианты. Обычные, начальные и центральные эмпирические моменты.
- •23. Условные эмпирические моменты. Отыскание центральных моментов по условным. Метод произведения.
- •21. Метод наименьших квадратов.
- •6. Распределение хи-квадрат, Стьюдента, Фишера
- •7. Интервальные оценки неизвестных параметров(дляMx)
- •8. Интервальные оценки неизвестных параметров(для dx)
- •9.Проверка статистических гипотез.
- •10. Гипотезы сравнения о равенстве мх при неизвестной дисперсии
- •16.Критерий Колмогорова.
- •17.Условные математические ожидания и их свойства.
- •18.Оснавная теорема регрессионного анализа.
- •19.Уравнения линейной регрессии.
- •20.Выборочные уравнения линейной регрессии.
- •15. Критерии ω² Мизиса-Смирнова.
- •1. Задачи математической статистики. Генеральная совокупность. Выборка.
- •3. Точечные оценки неизвестных параметров. Несмещенные, состоятельные, эмпирические оценки.
- •4. Методы получения оценок. Метод моментов.
- •5. Методы получения оценок. Метод максимального правдоподобия.
17.Условные математические ожидания и их свойства.
Пусть случайный
вектор (X,Y)
задан рядом распределения. Обозначим
через
![]()
|
y1 y2 … |
|
x1 x2 . . . |
p11 p12 … p21 p22 … . . . . . . |
p1. p2. . . . |
|
p.1 p.2 |
1 |
О. Условным математическим ожиданием случайной величины Y при условии, что случайная величина X приняла значение xi называется число
![]() Введем
случайную величину:
Введем
случайную величину:
![]() ,
если
,
если
![]() .
Эта случайная величина дискретная с
рядом распределения:
.
Эта случайная величина дискретная с
рядом распределения:
M(Y|X) |
M(Y|X=x1) |
M(Y|X=x2) |
… |
p |
p1. |
p2. |
… |
О.
Случайная величина M(Y|X)
называется условным математическим
ожиданием Y
при условии X.
![]()
Свойства условного математического ожидания:
1. M(C|X)=C.
![]() ,
отсюда
,
отсюда
![]()
2. M(Y1+Y2|X)=M(Y1|X)+M(Y2|X).
Справедлива формула полного математического ожидания:
18.Оснавная теорема регрессионного анализа.
Теорема (Основная теорема регрессионного анализа).
Наилучшим прогнозом
случайной величины Y
по случайной величине X
в среднем квадратическом смысле является
условное математическое ожидание
![]() Другими словами, если h(x)
– любой прогноз Y
по X,
то математическое ожидание
Другими словами, если h(x)
– любой прогноз Y
по X,
то математическое ожидание
![]()

19.Уравнения линейной регрессии.
О. Уравнение Y=f(X), где f(X)=M[Y|X] называется уравнением регрессии Y на X (прогноза Y по X).
Если обозначить через g(Y)=M(X|Y), то
О. Уравнение X=g(Y), где g(Y)=M(X|Y) называется уравнением регрессии X на Y (гипотеза Y по X)
О. Регрессия Y на X называется линейной, если f(X)=M(Y|X)=a0+a1X.(1) О. Регрессия X на Y называется линейной, если g(Y)=M(X|Y)=b0+b1Y.
Обозначим через
MX=a,
MY=b,
![]() ,
,
![]() и через r
коэффициент корреляции
и через r
коэффициент корреляции
![]()
Применим
математическое ожидание к обеим частям
уравнения (1)
![]()
![]() Вычтем из (1)-(2’)
Вычтем из (1)-(2’)
![]()
Применим операцию МО еще раз
![]()
![]() Из этого находим
постоянную
Из этого находим
постоянную
![]() .
Подставим в (3)
.
Подставим в (3)
![]() .
Искомое уравнение регрессии имеет вид:
.
Искомое уравнение регрессии имеет вид:
![]() -
уравнение линейной регрессии Y
на X.
Аналогично
-
уравнение линейной регрессии Y
на X.
Аналогично
![]() - уравнение линейной регрессии X
на Y.
- уравнение линейной регрессии X
на Y.
20.Выборочные уравнения линейной регрессии.
На практике, как
правило, иметься только выборка. Например,
(![]() ),…,(
),…,(![]() ).
Эмпирический коэффициент корреляции
r
является мерой тесноты линейной связи
между двумя случайными величинами. С
геометрической точки зрения это означает,
что чем теснее располагаются точки на
диаграмме рассеивания вокруг линии
регрессии, тем выше абсолютная величина
регрессии и наоборот. На рисунке 1-4
изображены несколько диаграмм рассеивания.
).
Эмпирический коэффициент корреляции
r
является мерой тесноты линейной связи
между двумя случайными величинами. С
геометрической точки зрения это означает,
что чем теснее располагаются точки на
диаграмме рассеивания вокруг линии
регрессии, тем выше абсолютная величина
регрессии и наоборот. На рисунке 1-4
изображены несколько диаграмм рассеивания.
![]()
![]()
![]()
![]()
Диаграмма на рис.1
указывает на отрицательную функциональную
связь (r=-1),
на рис.2- на относительно высокую степень
положительной корреляции (r≈0,8),
на рис.3- умеренную степень отрицательной
корреляции (r≈
-0,5), на рис.4 – отсутствие корреляции
(r=0).
По диаграмме рис.4 видно, что если
коэффициент корреляции равен 0 , то
независимо от того, чему равна величина
переменной X
, оцениваемая величина зависимой
переменной всегда равна
![]() .
.
Сначала , для построения диаграммы рассеивания строят корреляционное поле, т.е. наносят на плоскость все точки.
Если видят , что точки имеют тенденцию к линейной зависимости , начинают строить линейную регрессию.
11. Гипотезы сравнения о равенстве МХ при известной дисперсии.
Предположим, что
![]() известны. H0:
a1=a2.
В качестве оценок возьмем
известны. H0:
a1=a2.
В качестве оценок возьмем
![]() .
Критическая область
.
Критическая область
![]() .
.
![]() ,
т.к.
,
т.к.
![]() -несмещенная
оценка a1
-несмещенная
оценка a1
![]() .
Т.о
.
Т.о
![]() ,
аналогично
,
аналогично
![]()
![]() .
.![]() .
.
![]() Таким образом:
Таким образом:
![]() В качестве статистики критерия берем
случайную величину
В качестве статистики критерия берем
случайную величину
![]() (по лемме о
(по лемме о
12. Гипотезы сравнения о равенстве DX.
![]()
![]()
По лемме Фишера:
![]() В
качестве статистики нашего критерия
возьмем
В
качестве статистики нашего критерия
возьмем
![]()
![]()
![]()
![]() -заданный
уровень значимости.
-заданный
уровень значимости.
13. Критерии проверки гипотезы о равенстве нулю коэффициента корреляции.
![]() Предположим, что
имеется 2-мерная выборка
(x1,y1),(x2,y2),…,(xn,yn)
наблюдений случайного вектора (X,Y).
Предположим, что
имеется 2-мерная выборка
(x1,y1),(x2,y2),…,(xn,yn)
наблюдений случайного вектора (X,Y).
В качестве оценки
дисперсии возьмем:
![]() ср.
кв. откл.
ср.
кв. откл.
![]() ,
,![]() .
MX
заменяем оценкой
.
MX
заменяем оценкой
![]()
Выборочный
коэффициент корреляции:
![]() При больших n
При больших n
![]() можно показать, что
можно показать, что
![]() Проверим
Проверим
14. Критерии согласия χ² – Пирсона.
В критерии X2-
Пирсона в качестве меры отклонения
теоретической функции распределения
F(x)
от эмпирической функции распределения
Fn(x)
выбирается величина
![]()
![]()
![]()
Обозначим через
![]() ,
,
![]() -
число выборочных значений, попавших в
интервал
-
число выборочных значений, попавших в
интервал
![]() ,
,
![]()
Теорема (Пирсона).
Пусть , тогда
 ,
где случайная величина
,
где случайная величина
 имеет распределение X2
с (k-1)
степенью свободы.
имеет распределение X2
с (k-1)
степенью свободы.
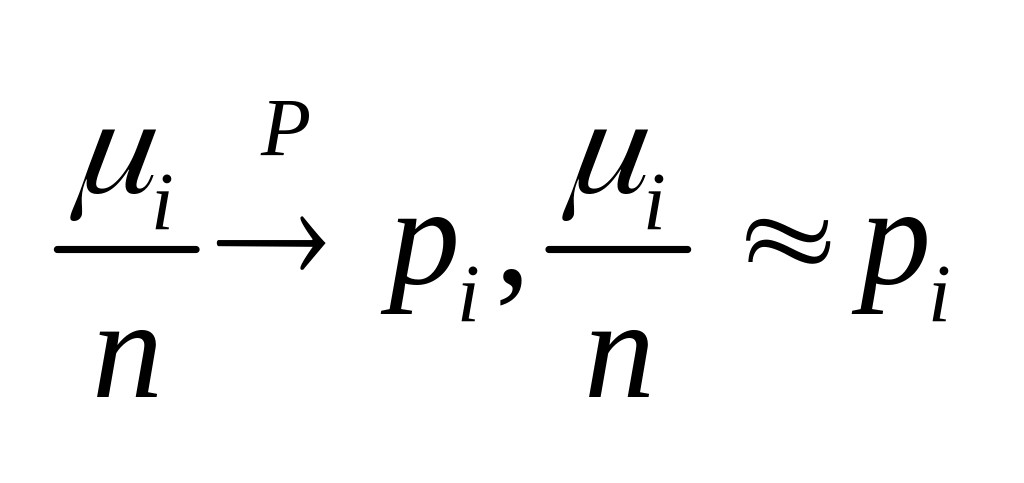 ,
тогда
,
тогда
 -
мало
-
мало X2
– небольшое число. Если предположим,
что H0
– верна, то
X2
– небольшое число. Если предположим,
что H0
– верна, то
