8. Интервальные оценки неизвестных параметров(для dx)

Опр. Случайные величины _н= _н( ) и , являющиеся функциями от выборочных значений, называются соответственно нижним и верхним двусторонними доверительными пределами для неизвестного параметра с надежностью (коэффициентом доверия, доверительной вероятностью) P (0,5<P<1) (или с уровнем значимости ), если для доверительного интервала вероятность . (1) При этом интервал называется двусторонним доверительным интервалом для параметра .

Замечание 2. В соотношение (1) случайными являются и , - число. Замечание 3. Пусть - точечная оценка параметра . Если - доверительный интервал. Тогда - точность интервальной оценки. Предположим, что - выборка из нормального распределения генеральной совокупности с параметрами .

1.Пусть - известно. Построить интервальную оценку для . - неисправленная выборочная дисперсия. .

9.Проверка статистических гипотез.

Предположим, что x₁,…,x_n – выборка из генеральной совокупности с функцией распределения F(x). F(x) может быть полностью неизвестна, тогда можно поставить следующую гипотезу: H₀: F(x)=F⁰(x), где F⁰(x) – конкретная функция распределения. Если вид функции распределения известен с точностью до каких-то m неизвестных параметров. Тогда гипотеза - заданные числа. Пусть x₁,…,x_n - берется из нормальной генеральной совокупности.

Допустим -известно и оно равно 1, т.е. ГС ~ N(a,1). Тогда или .

Пусть известно a=0, т.е. выборка берется из . или . Пусть a и неизвестны: или Подчеркнутые гипотезы называются простыми, поскольку задают единственную точку в пространстве параметров. Если гипотеза задает 2 и большее число точек в пространстве, то такая гипотеза называется сложной. H₀ – основная или нулевая гипотеза. H₁ – конкурирующая гипотеза или альтернативна.

Пусть X- выборочное пространство, т.е. это множество возможных значений вектора . Для построения критерия проверки гипотезы в выборочном пространстве выбирается критическая область

10. Гипотезы сравнения о равенстве мх при неизвестной дисперсии

Предположим, что x₁,x₂,…,x_n1 и y₁,y₂,…,y_n2 – две независимые выборки из нормальной генеральной совокупности с параметрами соответственно.

2. -неизвестно H₀: a₁=a₂.

По лемме Фишера:

-независимы и имеют стандартное нормальное распределение. ;

. -отношение Стьюдента. В качестве статистики возьмем:

- отношение Стьюдента.

16.Критерий Колмогорова.

Имеется выборка x₁,…,x_n и H₀: F(x)=F⁰(x). В качестве меры отклонения теоретической функции распределения F(x) берется .

Теорема (Колмогорова).

Если F(x) непрерывна, то . Имеются таблицы процентных точек распределения Колмогорова.

- процентная точка распределения Колмогорова, соответствующая уровню значимости или .

Алгоритм:

1. Считаем .

2. Если , то H₀ отвергается.

Если , то H₀ согласуется с экспериментальными данными.

Поэтому вероятность того, что

, . , где - уровень значимости. - искомый ДИ.

2. Пусть - не известно. Построить ДИ для . . По Лемме Фишера . ; ,

, . , .

- искомый ДИ.

таким образом, что если , то нулевая гипотеза H₀ отвергается, т.е. принимается гипотеза H₁, а если не попадает в область K, т.е. , то H₀ – принимается. Обычно K выбирается следующим образом: D=D(x₁,x₂,…,x_n) - некоторая функция от выборочных ранных значений, т.е. случайная величина. Обычно критическая область K выбирается одним из следующих 3-х способов: 1) односторонние критические области. 2) . 3) двусторонняя критическая область

О. Случайная величина D=D(x_1,x₂,…,x_n) называется статистикой критерия.

Ошибки:

1) Ошибка 1-го рода возникает, если H₀ – отвергается при условии, что H₀ – верна. -вероятность ошибки 1-го рода.

О. Вероятность ошибки 1-го рода называется уровнем значимости критерия.

2) Ошибка 2-го рода возникает тогда, когда H₀ принимается, хотя она неверна (т.е. верна H₁). -вероятность ошибки 2-го рода. Одновременно и невозможно. Если увеличивать, то будет уменьшаться и наоборот.

;

.

Если гипотеза H₀ отвергается. Если гипотеза H₀ согласуется с экспериментальными данными. ;

.

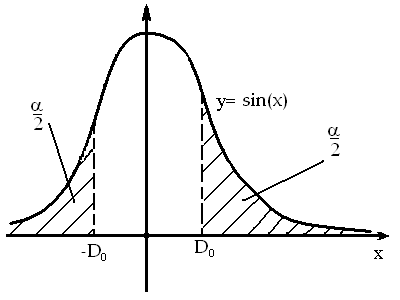
D₀-% точка распределения Стьюдента, .

Теорема1. 1) Пусть случайные величины - независимы и имеют нормальное распределение. Тогда СВ также имеет нормальное распределение.

2) Если случайная величина X имеет нормальное распределение, то при любых действительных А и В ( ), случайная величина Y=AX+B также имеет нормальное распределение. Предположим, что - выборка из генеральной совокупности с параметрами распределения . По теореме имеет нормальное распределение.

Пусть , В=0. - также имеет нормальное распределение.

, т.к. - несмещенная оценка, . ~ .

Следствие: Если - выборка из нормальной ГС с параметрами , то СВ ~ .

Предположим, что имеется выборка из нормальной генеральной совокупности с параметрами . Оценками величины -

Лемма: Если - выборка из нормальной генеральной совокупности с параметрами , то случайная величина

. Лемма Фишера: Если - выборка из нормальной генеральной совокупности с параметрами , то случайные величины и - независимы, причем .

Следовательно, получаем искомый ДИ: ,

где - точность оценки.

2. Пусть - неизвестно. Надо построить ДИ для .

~N(0,1). С другой стороны, по лемме Фишера: . Отсюда . - отношение Стьюдента с n-1 степенью свободы. . Здесь , где - уровень значимости для процентных точек. - искомый ДИ.

По лемме Фишера величина , => имеет распределение с степенями свободы, т.к. n-r= . Можно показать, что если выполняется гипотеза Н₀, т.е. , то и независимы и , => при выполнении гипотезы Н₀ величина (4) имеет распределение Фишера с r-1, n-r степенями свободы. Величина (4) может использоваться для проверки гипотезы о равенстве мат. ожиданий . Если эта гипотеза верна, то и явл. состоятельными оценками одной и той же СВ а и, =>, близки между собой, а величина мала. Если различны, то и сближаются с разными мат. ожиданиями: , и, =>, сумма должна принимать большие значения. Независимо от предложения о рав-ве , знаменатель в (4) остается оценкой σ². Это значит, что при увеличении расхождения между величина (4) в среднем должна принимать большие значения. Статистический критерий формулируется следующим образом: если , то гипотеза отвергается. Здесь нах-ся по таблице распределения Фишера с уровнем значимости α и числами степеней свободы r-1, n-r.

Обычные, начальные и центральные эмпирические моменты.

Для вычисления основных хар-к выборки удобно пользоваться эмпирическими моментами, определения кот. аналогичны определениям соотв. теоретических моментов. В отличие от теоретических, эмпирические моменты вычисляют по данным наблюдений. Опр.: Обычным эмпирическим моментом порядка к наз. среднее значение к-х степеней разностей : где - наблюдаемые варианты, -частоты вариант, n= -объем выборки, С - произвольное постоянное число( ложный нуль). Опр.: Начальным эмпирическим моментом порядка к наз. обычный момент порядка к при С=0: В частности т.е. начальный эмпирический момент первого порядка равен выборочной средней. Опр.: Центральным эмпирическим моментом порядка к наз. обычный момент порядка к при : ; - выборочная дисперсия.

соседними вариантами; практически же третий столбец заполняется так: в клетке строки, содержащей выбранный ложный нуль, пишут 0 ; в клетках над 0 пишут последовательно -1, -2, -3 и т. д., а под 0 – 1,2, 3 … 4) умножают частоты на условные варианты и записывают их произведение

в 4-ый столбец; сложив все полученные числа, их сумму помещают в нижнюю клетку столбца; 5) умножают частоты на квадраты условных вариант и записывают их произведение в 5-ый столбец; сложив все полученные числа, их суму помещают в нижнюю клетку столбца; 6) умножают частоты на квадраты условных вариант, увеличенных на единицу, и записывают произведения в 6-ой контрольный столбец; сложив все полученные числа, их сумму помещают в нижнюю клетку столбца. Замечание1. Целесообразно отдельно складывать отрицат. числа 4-го столбца (их суму записывают в клетку строки, содержащей ложный нуль) и отдельно положит. числа ( их сумму записывают в предпоследнюю клетку столбца); тогда Замечание2. При вычислении произведений 5-го столбца целесообразно числа 4-го столбца умножить на 3-го столбца. Замечание3.6-ой столбец служит для контроля вычислений: если сумма = , то вычисления проведены правильно. После заполнения таблицы и проверки правильности вычислений, вычисляются условные моменты: И вычисляют выборочные среднюю и дисперсию по формулам: .

выборочный коэффициент корреляции. Можно значительно упростить расчет, если перейти к условным вариантам (при этом не изменяется)

; . В этом случае выборочный коэффициент корреляции вычисляют по формуле: Величины можно найти методом произведений. Остается вычислить , где - частота пары условных вариант (u, ). Справедливы формулы