Векторное поле. О. Векторные линии и векторные трубки

О. Если каждой точке Р области V₂ трехмерного пространства поставлен в соответствие определенный вектор a(P)=a_xi + a_yj + a_zk, то говорят, что в области V₂ задано векторное поле, Определяемое векторной функцией a(P). Частные случаи:

Однородное поле. О. Векторное поле называется однородным, если a(P) – постоянный вектор, т.е. a_x,a_y,a_z – постоянные величины. Пример: a(P)=4i + 3j – 2k.

Плоское поле. О. Вект. поле наз. плоским, если в выбранной системе координат проекции вектора не зависят от одной из трех переменных x, y, или z и одна из проекций a_x,a_y или a_z равна нулю. Пример a(P)=a_x(x,y)i + a_y(x,y)j.

О. Векторной линией векторного поля a(Р) называется линия, в каждой точке которой направление касательной к ней совпадает с направлением вектора a, соответствующего этой точке. О. Семейством векторных линий векторного поля называется система дифференциальных уравнений вида

О. Векторной трубкой наз. пов-сть,

образованная векторными линиями, проходящими через точки некоторой лежащей в поле замкнутой кривой, не совпадающей с какой-либо векторной линией

Поток векторного поля. О. Вычисление.

О. Потоком векторного поля a(P)через поверхность σ называется интеграл, по поверхности от скалярного произведения вектора поля на единичный вектор нормали к поверхности K= . Если a(P) – поле скоростей текущей жидкости, то интеграл выраждает поток жидкости через поверхность σ.

K= = a_xcosα + a_ycosβ + a_zcosγ)dS = _xdydz + a_ydxdz + a_zdxdy.

K= _n(P)dS. Если на некотором участке a_n(P)=const, то K=a_nQ, где Q – площадь участка поверхности σ.

Вычислить поток можно 2-мя способами: 1. Методом проектирования поверхности на 3 координатные плоскости: Пусть D₁, D₂, D₃ – проекции плоскости (которая дана) на координатные плоскости (Oxy), (Oxz) и (Oyz), тогда поверхностный интеграл II рода сводится к сумме 3-х интегралов по областям D₁, D₂, D₃. 2. Методом перехода к поверхностному интегралу 1 рода (или с пом. нормали): находится единичный вектор нормали в виде ±{cosα, cosβ, cosγ}, ± берется в зависимости от выбранной стороны поверхности. Далее единичный вектор нормали записывается в векторной форме (т.е. чтоб были i, j, k). Находим dS=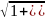 dxdy, а потом подставляем все в формулу для потока K= _xdydz + a_ydxdz + a_zdxdy.

Дивергенция векторного поля. О. Выч. Теорема г-о

О. Дивергенцией векторного поля a(P) называется предел отношения потока вектора через замкнутую поверхность σ, окружающую точку Р, к объему, ограниченному этой поверхностью, при условии, что вся поверхность стягивается в точку Р, т.е. что V→0

diva=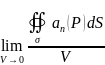 = 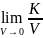. Лемма. Пусть a_x,a_y,a_z – непрерывные функции вместе со своими частными производными. Дивергенция Векторного поля a(P)=a_xi + a_yj + a_zk выражается формулой div a(P) = + + .

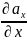Т. Г-О. Поток векторного поля a(P)=a_xi + a_yj + a_zk через замкнутую поверхность σ, лежащую в поле, в направлении ее внешней нормали, равен тройному интегралу по области Т, ограниченной этой поверхностью, от дивергенции этого векторного поля:

K= = (свойства дивергенции на обороте)