Изолированные особые точки и их классификация

О. Пусть f(z) – однозначная и аналитическая функция в вырожденном кольце D:

0<|z-z₀|<R и пусть существует комплексное число z₁ такое, что если положить f(z₀)=z₁, то f(z) станет аналитической во всем круге |z-z₀|<R. В этом случае точка z₀ называется правильной точкой функции f(z). Иначе, в правильных точках не нарушается аналитичность. Точки, в которых нарушается аналитичность функции, называются особыми. О. Если в достаточной близости к особой точке z₀ нет других особых точек, то z₀ называется изолированной особой точкой, иначе, z₀ – изолированная особая точка функции f(z), если f(z) – однозначная аналитическая функция в кольце 0<|z-z₀|<R, где z₀ – особая точка. Логически возможны и исключают друг друга 3 случая:

1-й случай. Если главная часть разложения функции в ряд Лорана в точке Z₀ отсутствует, т.е. ряд имеет вид 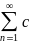_n (z - z₀)ⁿ, то изолированная особая точка Z₀ называется устранимой. Либо если функция f(z) – аналитическая в окрестности точки z=z₀ и ограничена по модулю в этой окрестности, т.е. существует конечный предел 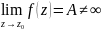2-й случай. Если главная часть разложения функции в ряд Лорана в точке Z₀ содержит лишь конечное число членов (иначе, содержит конечное число членов с отрицательными показателями), т.е. ряд имеет вид

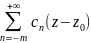ⁿ = 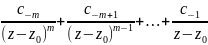+ c₀+c₁(z-z₀) + c₂(z-z₀)+… то изолированная особая точка Z₀ называется полюсом порядка m≥1. Либо если f(z) –аналитическая в окрестности точки z=z₀ и справедливо равенство .

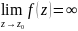3 случай. Если главная часть разложения функции в ряд Лорана в точке Z₀ содержит бесконечное число членов, т.е. ряд имеет вид: 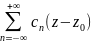ⁿ, то изолированная особая точка Z₀ называется существенно особой точкой. Либо если при z, близких к точке Z₀, |f(z)| не остается ограниченным, но функция не стремится к бесконечности при z стремящемся к Z₀, т.е. 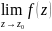не существует.

Ряд Тейлора

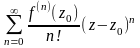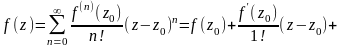
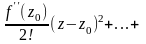
О. Пусть дана функция f(z), аналитическая в некоторой окрестности точки z₀. Ряд наз. рядом Тейлора ф-ии f(z) и внутри круга сход-ти выполн. рав-во: 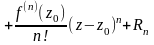. Т. (т. Тейлора). Всякая аналитическая функция f(z) внутри круга с центром в точке z₀ и радиусом R, т.е |z – z₀| < R, может быть разложена внутри этого круга в степенной ряд Тейлора по степеням (z – z₀) : 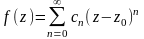, коэффициенты c_n которого определяются по формулам: 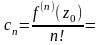(по интегральной формуле Коши) = 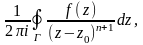где Г – какая-ниб. фиксированная концентрическая окружность радиуса r < R, т.е. лежащая внутри круга сходимости.

Ряд Лорана

Рядом, обобщающим понятие степенного ряда, является ряд Лорана. Рассмотрим разложение в ряды двух функций: 1-ый ряд:

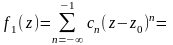
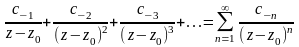
2-ой ряд:

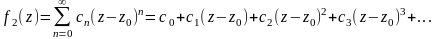
Область сходимости 1-го ряда, если она существует, определяется неравенством:

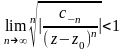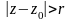, отсюда, , где (*)

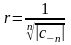Область сходимости 2-го ряда, если она существует, определяется неравенством:

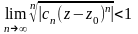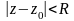, отсюда, , где 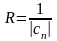(**), причем

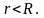
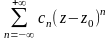
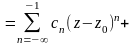
О. Рядом Лорана называется ряд ⁿ, представляющий собой сумму двух рядов: 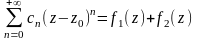, при этом 1-й ряд ­– f₁(z) - называется главной частью, а 2-й ряд ­– f₂(z) – правильной частью ряда Лорана.

Вычисление Вычетов. Определение (Т. дальше…)

О. (первое определение вычета). Если f(z) аналитическая функция в некоторой окрестности точки Z₀, за исключением, может быть, самой точки Z₀, то вычетом функции f(z)относительно точки Z₀ называется число, равное значению интеграла: выч[f(z);z₀] =

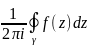= , где γ – некоторый простой замкнутый контур, лежащий в области аналитичности функции f(z) и содержащий внутри себя только 1 особую (.) Z₀.

О. (второе определение вычета). Коэффициент при (–1) –ой степени разложения функции f(z)в ряд Лорана наз. вычетом функции f(z) относ. (.) Z₀: выч[f(z);z₀] = c_-1

Формулы для нахождения вычетов:

1. Пусть Z₀– полюс первого порядка функции f(z). Тогда главная часть ее разложения в ряд Лорана содержит одно слагаемое: f(z) = 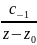+ c₀+c₁(z-z₀) +…. Умножим обе части данного равенства на (z – z₀) и найдем предел при z → z₀:

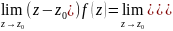c_-1 + (z – z₀)c₀ + c₁(z – z₀)² +…) = c_-1. Следовательно, имеем выч[f(z);z₀] = 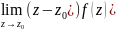. (Если f(z) = 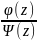, то выч[f(z);z₀] = )

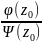2. Пусть Z₀ – полюс порядка m≥2 функции f(z). Тогда выч[f(z);z₀] = 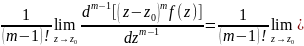[( )^mf(z)]^(m-1).

3. Пусть Z₀ – устранимая особая точка функции f(z). Тогда главная часть ее разложения в ряд Лорана отсутствует: выч[f(z);z₀] = 0.

4. Пусть Z₀ – существенно особая точка функции f(z), тогда вычет относительно ее можно найти только по разложению функции в ряд Лорана, т.к. главная часть содержит бесконечное число членов: выч[f(z);z₀] = c_-1.

5. Пусть z₀=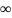 – изолированная особая точка функции f(z), Тогда вычетом функции относительно точки z₀= является коэффициент при (–1)-ой степени разложения функции в ряд Лорана, взятый с противоположным знаком: выч[f(z); ] = -c_-1.