Ортогональный и ортонормированный базис

Ортогональный (ортонормированный) базис - ортогональная (ортонормированная) система элементов линейного пространства со скалярным произведением, обладающая свойством полноты.

Конечномерный случай

Ортогональный базис — базис, где все векторы попарно ортогональны.

Ортогональный базис из единичных векторов называется ортонормированным.

Скалярное произведение каждой пары базисных векторов равно нулю, когда они не совпадают ( ), и равно единице при совпадающем индексе.

Бесконечномерный случай

Ортогональный базис — система попарно ортогональных элементов e₁,e₂,...,e_n,... гильбертова пространства X такая, что любой элемент   однозначно представим в виде сходящегося по норме ряда x = ,

- ряд Фурье элемента x по системе {e_n}.

Если | e_n | = 1 - ортонормированный базис. В этом случае числа a_n, называются коэффициентами Фурье элемента x по ортонорм-му базису {e_n}, имеют вид a_n = (x,e_n).

Понятие меры. Измеримые функции. Простые функции. Ортогональные функции

Мерой множества на плоскости называется его площадь. Внешней мерой ^*(A) множества А называется нижняя грань меры элементарных множеств, включающих множество А. Измеримые ф-ии. Пусть X и Y - два произвольных множества и в этих множествах выбраны системы подмножеств S_X и S_Y соответственно. Функция f:XY называется (S_X,S_Y)-измеримой, если для любого подмножества АS_Y его прообраз содержится в S_X : f ^-1(A) S_X. Простые ф-ии. Функция f(x), определенная на некото­ром пространстве Х с заданной на нем мерой, называется про­стой, если она измерима и

принимает не более, чем счетное число значений.

Ортогональные ф-ии. Функции φ₁(x) и φ₂(x) называются ортогональными на |a,b|, если (φ_1,φ₂)=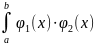 dx=0.

Мера Лебега. Свойства меры Лебега. Интеграл Лебега

Множество А называется измеримым по Лебегу, если для любого  > 0 найдется такое элементарное множество B, что *(A  B) < . Функция *, рассматриваемая только на измеримых множествах, называется лебеговой мерой .

Свойства меры Лебега. 1) мера любого множества неотрицательна: m (A)D ³ 0;

2) мера суммы A=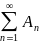 конечной или счётной системы попарно непересекающихся множеств A₁, A₂..., A_n... равна сумме их мер: m(A)=

3) при перемещении множества как твёрдого тела его мера не меняется.

Интеграл Лебега. Интегралом Лебега по множеству А от простой функции f(x) называется сумма ряда I =  y_n (A_n) , где A_n = {xA | f(x) = y_n}.

Нормированные пространства. Норма. Примеры

Нормированным векторным пространством называется пара  , где V — векторное пространство, а   — норма в V. Норма — функция, заданная на векторном пространстве и обобщающая понятие длины вектора или абсолютного значения числа.

Примеры нормированных пространств. 1. Конечномерные нормированные пространства.

Вещественная прямая   является нормированным пространством, если в качестве нормы взять модуль вещественного числа.

В действительном конечномерном пространстве   норму можно ввести нескольким способами. Наиболее широко известна Евклидова норма:

. Другие возможные нормы: , .

В комплексном n-мерном пространстве   норму можно ввести следующим образом:

||x|| = 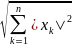. 2. Пространство непрерывных функций. В простр-ве непрерывных на отрезка [a,b] функций C[a,b] норму можно задать формулой ||f|| = .
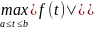