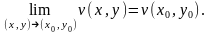- •Понятия фкп. Выражения для х и у.
- •Основные Элементарные функции
- •Предел и непрерывность фкп
- •Дифференцируемость. Условие Коши-Римана
- •Гармонические функции. Гармонические пары.
- •Определение и св-ва аналитических функций
- •Конформность отображения посредством гармонической пары и аналитической функции. Геометрический смысл модуля и аргумента производной.
- •Линейная функция
- •Простейшая дробно-линейная функция
- •Степенная функция
- •Дробно-линейная функция
- •Интегрирование по комплексному аргументу
- •Теорема Коши. Интегральная формула Коши
- •Ряды с комплексными членами
- •Изолированные особые точки и их классификация
- •Ряд Тейлора
- •Ряд Лорана
- •Основные теоремы о вычетах
- •Скалярное поле. Определение. Линии и поверхности уровня.
- •Скалярное поле. Производная по направлению.
- •Скалярное поле. Градиент
- •Векторное поле. О. Векторные линии и векторные трубки
- •Поток векторного поля. О. Вычисление.
- •Дивергенция векторного поля. О. Выч. Теорема г-о
- •Циркуляция векторного поля. О. Вычисление
- •Ротор векторного поля. О. Выч. Теорема Стокса
- •Оператор Гамильтона. Диф-ые операции II порядка
- •Специальные виды векторных полей. Соленоидальое
- •Специальные виды векторных полей. Потенциальное
- •Специальные виды векторных полей. Лапласово (гармоническое)
- •Теорема о разложении векторных полей.
- •Применение вычетов к вычислению контурных интегралов
- •Применение тфкп
- •Определение функционального анализа. Предмет функционального анализа.
- •Определение евклидова пространства
- •Определение линейных пространств. Аксиомы. Свойства
- •Линейные операторы. Действия с лин. Операторами
- •Базис и матрица линейного оператора Собственные значения и собственные векторы линейного оператора
- •Квадратичные формы. Матрица квадратичной формы. Пример.
- •Ортогональный и ортонормированный базис
- •Понятие меры. Измеримые функции. Простые функции. Ортогональные функции
- •Мера Лебега. Свойства меры Лебега. Интеграл Лебега
- •Нормированные пространства. Норма. Примеры
- •Метрические пространства. Метрика. Примеры. Сжатые отображения
- •Ортогональный и ортонормированный базис. Процесс Ортогонализации. Сопряженные векторы в евклидовом пространстве.
- •Дифференциальные уравнения с частными производными
- •Основные уравнения математической физики
- •Явная и Неявная разностная схема
Понятия фкп. Выражения для х и у.
О. Пусть дано некоторое множество М комплексных чисел z, например, некоторая область на плоскости Гаусса (z). Если каждому элементу z из этого множества по некоторому закону f поставлено в соответствие одно, вообще говоря, комплексное число ω = f(z), то говорят, что на множестве М определена функция комплексного переменного (ФКП) – ω. ω = f(z)
Область определения ФКП – множество М точек плоскости Гаусса(z).
О. Область М (на плоскости, в пространстве) называется односвязной, если любой замкнутый контур, лежащий в этой области, можно непрерывно стянуть в точку, не выходя при этом за пределы области (иначе, область без «дырок»).
Евклидово
пространство – метрическое пространство,
в котором для любых двух точек x
и y
определено число ρ(x,
y)
– расст. от х
до y
или метрика
так, что выполняются аксиомы: 1) ρ(x,
y)
= ρ(y,
х), 2) ρ(x,
y)
> 0 при x y;
ρ(x,
х)
= 0 при любых х,
3) ρ(x,
y)
+ ρ(y,
z)
y;
ρ(x,
х)
= 0 при любых х,
3) ρ(x,
y)
+ ρ(y,
z) ρ(y,
z).
ρ(y,
z).
Рассмотрим
комплексное число z
= x
+ iy,
тогда значение функции в точке z
равно ω
= f(z)
= u
+ iv,
Re[f(z)]
= u
– действительная часть, Im[f(z)]
= v
– мнимая часть функции ω
= f(z).
Т.о. при переходе от точки z
к точке z1
меняются
координаты
x
и y
на плоскости
Гаусса, следовательно, меняется и
значение f(z),
т.е. изменяются u
и v,
следовательно, u
и v
тоже
функции
переменных x
и y:
ω = f(z)
= u(x,
y)
+ iv(x,
y).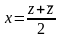

Основные Элементарные функции
1.
Дробно-рациональная ω= f(z)=
 .
.
2. Показательная функция ω = f(z) = ez = ex(cosy + isiny)
3.
Триг. функции. C
помощью формулы Эйлера sin
z
=
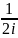 (eiz-e-iz);
cosz=
(eiz-e-iz);
cosz=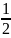 (eiz+e-iz);
(eiz+e-iz);
4. Гиперболические функции: shz= (ez-e-z); chz= (ez+e-z);
5.
Логарифмические функции.
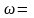 Ln
z
Ln
z
 ,
, .
.
6. Общая степенная функция ω=za. а) Если а = n – натуральное число, то степенная функция ω = zn определяется как: ω = zn = rn(cosnφ + isin nφ).
б)
если a=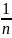 ,
где n
,
где n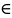 N,
то ω =
N,
то ω =
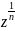 =
=
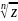 =
=
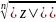
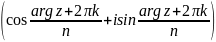 ,
k
= 0,1,2,…,n-1.
в)
Если a=
,
k
= 0,1,2,…,n-1.
в)
Если a=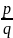 ,
где p,q
N,
то
,
где p,q
N,
то
ω
=
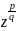 =
=
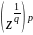 =
=
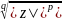
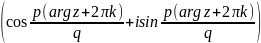 ,
k = 0,1,2,…,n-1.
,
k = 0,1,2,…,n-1.
г)
Степенная функция ω = zα,
где α = α + iβ
– произвольное комплексное число.
Тогда степенная функция ω = za
= zα+βi
определяется
как za
=
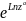 =eaLnz.
=eaLnz.
7. Общая показательная функция ω = az. ω = az = ezLna, a C
8.
Обратные тригонометрические функции:
Arcsinz
= -iLn(iz+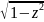 );
);
Arcsosz=-iLn(z+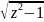 );
Arctgz =
);
Arctgz =
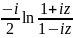 ,
(z
,
(z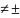 i);
Arcctz =
i);
Arcctz = ,
(z
i).
,
(z
i).
9. Обратные гиперболические функции:
Arshz
= Ln(z+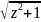 );
Archz = Ln(z+
);
Arhz =
Ln
);
Archz = Ln(z+
);
Arhz =
Ln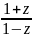 .
.
Предел и непрерывность фкп
О.
Число A
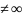 называется пределом функции ω = f(z)
при z
→ z0
и обозначается
называется пределом функции ω = f(z)
при z
→ z0
и обозначается
A
=
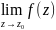 ,
если для любого положительного ε
найдется число δ = δ(ε) > 0 такое, что
для всех z
,
если для любого положительного ε
найдется число δ = δ(ε) > 0 такое, что
для всех z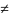 z0,
удовлетворяющих неравенству |z
– z0|
<δ выполняется неравенство |f(z)
– A|
<
z0,
удовлетворяющих неравенству |z
– z0|
<δ выполняется неравенство |f(z)
– A|
<
 .
О (первое
определение непрерывности функции в
точке).
Функция ω = f(z)
называется непрерывной в точке z0,
принадлежащей ее области определения,
если
.
О (первое
определение непрерывности функции в
точке).
Функция ω = f(z)
называется непрерывной в точке z0,
принадлежащей ее области определения,
если
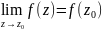 .
Отсюда можно записать, что для
непрерывности функции в точке должно
выполняться равенство нулю разности:
.
Отсюда можно записать, что для
непрерывности функции в точке должно
выполняться равенство нулю разности:
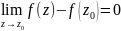 .
.
О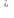 (второе
определение непрерывности функции в
точке).
Функция ω = f(z)
называется непрерывной в точке z0,
принадлежащей ее области определения,
если
(второе
определение непрерывности функции в
точке).
Функция ω = f(z)
называется непрерывной в точке z0,
принадлежащей ее области определения,
если
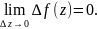 О.
Функция ω = f(z)
называется непрерывной на некотором
множестве, если она непрерывна в каждой
точке этого множества.
О.
Функция ω = f(z)
называется непрерывной на некотором
множестве, если она непрерывна в каждой
точке этого множества.
Т. (необходимое и достаточное условие непрерывности). Для непрерывности ФКП необходима и достаточна непрерывность составляющих ее функций:
ω
= f(z)
– непрерывна
 u
= u(x,
y);
v
= v(x,
y)
– непрерывны.
u
= u(x,
y);
v
= v(x,
y)
– непрерывны.
Замечание.
Равенство
эквивалентно двум равенствам: