6. Трехмерные преобразования

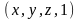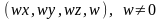Однородные координаты в трехмерном случае записывают в виде или . Таким образом, любая точка пространства, кроме начала координат, может быть задана четверкой одновременно не равных нулю чисел. Матрицы преобразований в этом случае имеют размер 4х4.

Матрицы поворота.

Повороты вокруг осей абсцисс, ординат и аппликат на угол α соответственно имеют вид:

, , .

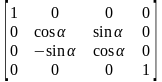Матрицы масштабирования и переноса имеют вид:

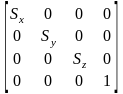и .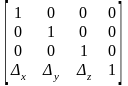

Обратите внимание, что все матрицы преобразования не вырождены.

Пример.

Выполнить поворот точки на угол α вокруг прямой L, проходящей через точку (a,b,c), параллельной вектору (l,m,n). Считаем, что вектор единичной длины.

1 шаг.

Сдвиг точки в начало координат (или начала координат в точку (a,b,c)):

.

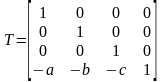Теперь прямая L проходит через начало координат.

2 шаг.

Совместим ось аппликат с прямой, вокруг которой нужно выполнить поворот.

1. Сначала выполним поворот вокруг оси абсцисс так, чтобы прямая лежала в плоскости z0x (или поворачиваем систему координат). Угол поворота равен углу между осью аппликат и проекцией L₁ прямой на плоскость z0y.

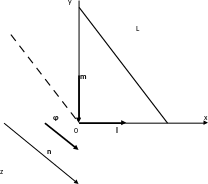
Рис. 1. Схема определения угла первого поворота

Вектор проекции имеет направляющую (0,m,n). Тогда косинус искомого угла определяется так:

.

Матрица поворота имеет вид:

.

Если пересчитать координаты вектора, параллельно которой лежит теперь прямая, получим:

.

Нетрудно проверить, что вектор имеет единичную длину.

2. Выполним поворот вокруг оси ординат на угол.

Теперь прямая лежит на плоскости z0x.

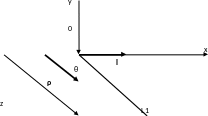
Рис. 2. Результат поворота вокруг оси абсцисс.

Угол поворота вокруг оси ординат определяется соотношениями:

.

Матрица поворота имеет вид:

.

3 шаг.

Теперь можем выполнить поворот на угол α вокруг прямой L. Прямая совпадает с осью аппликат, поэтому матрица поворота имеет вид:

.

Все необходимые операции поворота выполнены:

.

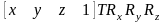Теперь нужно вернуть в исходное положение систему координат. При этом все преобразования системы координат нужно выполнять в обратном порядке.

4 шаг.

Выполняем обратный поворот вокруг оси ординат:

.

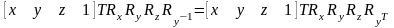Здесь мы пользуемся тем, что матрица ортогональная и ее обратная совпадает с ее транспонированной.

5 шаг.

Выполняем обратный поворот вокруг оси абсцисс:

.

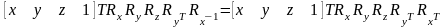Здесь опять пользуемся тем, что матрица 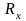ортогональная и ее обратная совпадает с ее транспонированной.

6 шаг.

Выполняем обратный перенос.

.

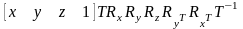Обратную матрицу 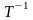вычислять не нужно. Она, как и следовало ожидать, равна:

.

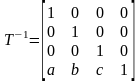Если нужно повернуть множество точек на угол α вокруг прямой L, проходящей через точку (a,b,c), параллельной вектору (l,m,n), то выгодно изначально вычислить одну матрицу преобразования

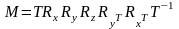
и умножить на эту матрицу все точки.

Точно также все сложные преобразования приводятся к композиции элементарных преобразований.

7. Трехмерные системы координат

На разных этапах обработки объектов используются различные системы координат. Используются следующие основные системы координат:

1. Координаты модели.

2. Мировые координаты.

3. Координаты камеры.

4. Координаты перспективы.

5. Экранные координаты.

Координаты модели (локальные координаты)

Объект описывают в его собственной системе координат и, только затем, переносят в реальное положение. При этом объектом может быть и часть рассматриваемого объекта. Суть описания в локальной системе координат заключается в том, что для каждого объекта локальная система наиболее удобна для описания его свойств.

Например, пусть рука робота описывается с помощью двух деталей (рис. 1).

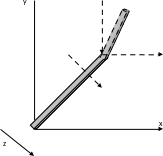
Рис. 1. Пример локальных систем координат объектов

Каждую часть руки (объект) удобно описывать в своей локальной системе координат.

СОГЛАШЕНИЯ

Существуют соглашения ориентации:

1. Передняя часть объекта ориентирована вдоль положительного направления оси z, а верх – вдоль положительного направления оси y.

2. Программное обеспечение само определяет первую главную ось (вдоль наибольшей длины) и согласовывает с положительным направлением оси y, а вторую главную ось согласовывает с положительным направлением оси z.

Первый способ предпочтительнее, так как главные оси объекта не всегда имеют максимальные длины.

Существуют соглашения масштабирования. Это связано с тем, что на этапе создания объекта часто используют нормализованные размеры. Например, и мяч и астероид на этапе создания на экране могут иметь одни и те же размеры.

Левая или правая система координат. Обе системы равноправны, нельзя только путаться затем в формулах. Это касается положительного направления оси z. Чаще всего используют левую систему координат, когда положительное направление оси z внутрь экрана.

Мировые координаты

Трехмерные модели объектов надо разместить в единой сцене, где правит система мировых координат. Если ранее координаты объекта были определены относительно локальной системы координат, то теперь нужно переопределить (не изменяя или сохраняя локальные координаты) их в мировых координатах. Это обычный перенос (или смещение) – то есть тривиальная операция. Если требуется выполнить поворот (или масштабирование) объекта, то его сначала поворачивают (или масштабируют) в локальных координатах и, только затем, переносят в мировые координаты.

Координаты камеры

Камеру располагают обычно в левой мировой системе координат. Характеристики камеры задают следующие параметры:

1. Положение определяют координатами (cam_x, cam_y, cam_z).

2. Ориентацию задают углами поворота (вокруг оси x – тангаж – α, вокруг оси y – рыскание – β, вокруг оси z – крен – γ). Для пояснения углов поворота приняли, что камера смотрит в положительном направлении оси z, верх камеры – в положительном направлении оси y. Конечно, камера может быть ориентирована и по-другому, но смысл и название углов остаются.

3. Поле обзора камеры ограничено в горизонтальном и вертикальном направлении в пределах 60-130°.

4. Имеются ближняя и дальняя плоскости отсечения, между которым находятся видимые для камеры объекты.

5. Плоскость проекции – это математическая плоскость, на которую проецируются изображения трехмерных объектов. Естественно, для нас эта плоскость совпадает с экраном дисплея.

Камера обычно располагается не в начале мировых координат. Для проецирования объектов на плоскость проекции удобнее, если мы перенесем начало координат в центр объектива камеры. При этом нужно выполнить такой же перенос всех видимых для камеры объектов реального мира.

Точно также камера практически всегда имеет ненулевые значения углов поворота. До поворота обязательно нужно переместить начало мировых координат в центр координат камеры. После этого можно повернуть мировые координаты и все видимые объекты так, чтобы углы поворота камеры оказались нулевыми, и камера смотрит в положительном направлении оси z, верх камеры – в положительном направлении оси y. При этом наиболее часто поворот выполняют последовательно сначала вокруг оси y, затем вокруг оси x, и только потом вокруг оси z. Это подобно тому, что человек при поиске поворачивает голову сначала влево-вправо, затем вверх-вниз, и только в последнюю очередь покачивает головой от плеча к плечу. Реже выполняют повороты в последовательности zyx. Можно поступать и по-другому – выполнять поворот сначала на максимальный угол.

Этапы преобразований координат

1. Определение объектов в локальных координатах.

2. Размещение объектов в мировых координатах. Описание в локальных координатах и описание в мировых координатах хранятся по отдельности.

3. Перевод мировых координат в координаты виртуальной камеры (рис. 2).

4. Обработка видимых объектов (или удаление скрытых объектов) – это будет рассмотрено позже.

5. Проецирование на плоскость проецирования (экран просмотра).

Плоскость проецирования

Для построения проекций наиболее важны угол обзора и расстояние просмотра. Для упрощения расчетов выберем угол обзора в 90°.

Рассмотрим расчет проекции (x_d,y_d,z_d) точки (x₀,y₀,z₀).

Вычислим значение x_d и y_d. Из правил о подобных треугольниках получаем:

,

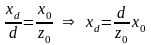Очевидно, что z_d=d.

Это проецирование в однородных координатах имеет следующий вид:

.

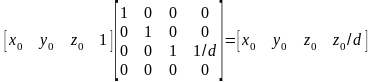Для перехода из однородных координат в декартовы, поделим координаты на :

.

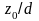На практике используют следующие два способа при выборе значения d. Условно эти способы можно назвать «нормализованный экран» и «естественный экран» просмотра.

8. Параллельное проецирование.

Параллельное проецирование можно рассматривать как частный случай центрального проецирования, когда центр проецирования удален в бесконечность, а проецирующие лучи параллельные. Положение проецирующих прямых относительно плоскости проекций определяется вектором направления проецирования. Получаемое при этом изображение называют параллельной проекцией объекта. При параллельном проецировании сохраняются свойства центрального и добавляются следующие:

1. проекции параллельных прямых параллельны между собой;

2. отношение отрезков прямой равно отношению их проекций;

3. отношение отрезков двух параллельных прямых равно отношению их проекций.

В свою очередь параллельные проекции подразделяются на прямоугольные, когда проецирующие лучи перпендикулярны плоскости проекций, и косоугольные, когда направление проецирования образует с плоскостью проекций угол не равный 90⁰.

Частным случаем параллельного проецирования является ортогональное проецирование. Проекция объекта, полученная с использованием этого метода, называется ортогональной. Ортогональному проецированию присущи все свойства параллельного и центрального проецирования и, кроме того, справедлива теорема о проецировании прямого угла: если хотя бы одна сторона прямого угла параллельна плоскости проекций, а вторая не перпендикулярна ей, то прямой угол на эту плоскость проецируется в прямой угол.

К проекционным изображениям в начертательной геометрии предъявляются следующие основные требования:

1. Обратимость – восстановление оригинала по его проекционным изображениям (чертежу) – возможность определять форму и размеры объекта, его положение и связь с окружающей средой.

2. Наглядность – чертеж должен создавать пространственное представление о форме предмета.

3. Точность – графические операции, выполненные на чертеже, должны давать достаточно точные результаты.

4. Простота – изображение должно быть простым по построению и допускать однозначное описание объекта в виде последовательности графических операций.

К счастью, эти требования распространяются не на все задачи компьютерной графики.

В машинной графике используют центральные (перспективные) и параллельные проекции.

В зависимости от взаимного положения плоскости проекции и координатных осей проекции делят на следующие виды.

Одноточечную центральную проекцию мы уже рассмотрели достаточно подробно. Далее эти наработки мы используем в качестве базы для изучения других видов проекций.

Ортографическая проекция – в общем случае, изображение какого-нибудь предмета на плоскости, посредством проектирования отдельных его точек при помощи перпендикуляров к этой плоскости. В этой проекции предметы представляются такими, какими они представлялись бы наблюдателю, смотрящему на них с бесконечного расстояния. Каждый план есть проекция местности на горизонтальную плоскость, проведенную через середину участка. В ортографической проекции иногда изображают и целые полушария земли.

В компьютерной графике при ортографической проекции плоскость проекции совпадает с одной из координатных плоскостей или параллельна ей. Например, матрица проецирования вдоль оси X на плоскость Y0Z имеет вид:

.

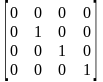Если плоскость проецирования параллельная плоскости Y0Z, то матрицу проецирования нужно умножить на матрицу переноса.

Тогда матрица проецирования вдоль оси X будет иметь вид:

.

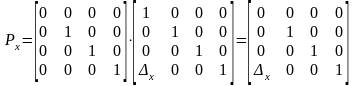Матрица проецирования вдоль оси Y имеет вид

.

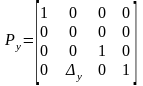Матрица проецирования вдоль оси Z имеет вид

.

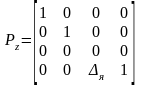Ортографическая проекция часто кажется немного странной, потому что объекты остаются того же самого размера, независимо от расстояния: это подобно просмотру сцены от отдаленной в бесконечность точки. Однако, ортонормированный просмотр очень полезен, потому что обеспечивает более «техническое» проникновение в сцену, делая ее проще, для определения пропорций.

Обычно ортогональную проекцию применяют для детального рассмотрения объекта с шести разных сторон. Можно, например, рассмотреть дом снизу, сверху, спереди, сзади, слева и справа - при этом направление проецирования совпадает с одной из осей координат. Пока нет отсечения невидимых граней имеет смысл рассматривать только проекции параллельно трех осей координат.

9. Отрезок проводится между двумя точками — (x₀,y₀) и (x₁,y₁), где в этих парах указаны колонка и строка, соответственно, номера которых растут вправо и вниз. Сначала мы будем предполагать, что наша линия идёт вниз и вправо, причём горизонтальное расстояние x₁ − x₀ превосходит вертикальное y₁ − y₀, т.е. наклон линии от горизонтали — менее 45°. Наша цель состоит в том, чтобы для каждой колонки x между x₀ и x₁, определить, какая строка y ближе всего к линии, и нарисовать точку (x,y).

Общая формула линии между двумя точками:

Поскольку мы знаем колонку x, то строка y получается округлением к целому следующего значения:

Однако, вычислять точное значение этого выражения нет необходимости. Достаточно заметить, что y растёт от y₀ и за каждый шаг мы добавляем к x единицу и добавляем к y значение наклона

которое можно вычислить заранее. Более того, на каждом шаге мы делаем одно из двух: либо сохраняем тот же y, либо увеличиваем его на 1.

Что из этих двух выбрать — можно решить, отслеживая значение ошибки, которое означает — вертикальное расстояние между текущим значением y и точным значением y для текущего x. Всякий раз, когда мы увеличиваем x, мы увеличиваем значение ошибки на величину наклона s, приведённую выше. Если ошибка превысила 0.5, линия стала ближе к следующему y, поэтому мы увеличиваем y на единицу, одновременно уменьшая значение ошибки на 1. В реализации алгоритма, приведённой ниже, plot(x,y) рисует точку, а abs возвращает абсолютную величину числа:

function line(x0, x1, y0, y1)

int deltax := abs(x1 - x0)

int deltay := abs(y1 - y0)

real error := 0

real deltaerr := deltay / deltax

int y := y0

for x from x0 to x1

plot(x,y)

error := error + deltaerr

if error >= 0.5

y := y + 1

error := error - 1.0

Проблема такого подхода — в том, что с вещественными величинами, такими как error и deltaerr, компьютеры работают относительно медленно. Кроме того, при вычислениях с плавающей точкой может накапливаться ошибка. По этим причинам, лучше работать только с целыми числами. Это можно сделать, если умножить все используемые вещественные величины на deltax. Единственная проблема — с константой 0.5 — но в данном случае достаточно умножить обе части неравенства на 2. Получаем следующий код:

function line(x0, x1, y0, y1)

int deltax := abs(x1 - x0)

int deltay := abs(y1 - y0)

int error := 0

int deltaerr := deltay

int y := y0

for x from x0 to x1

plot(x,y)

error := error + deltaerr

if 2 * error >= deltax

y := y + 1

error := error - deltax

Умножение на 2 для целых чисел реализуется битовым сдвигом влево.

Теперь мы можем быстро рисовать линии, направленные вправо-вниз с величиной наклона меньше 1. Осталось распространить алгоритм на рисование во всех направлениях. Это достигается за счёт зеркальных отражений, т.е. заменой знака (шаг в 1 заменяется на -1), обменом переменных x и y, обменом координат начала отрезка с координатами конца.

Реализация на C++:

void drawLine(int x1, int y1, int x2, int y2)

{

int deltaX = abs(x2 - x1);

int deltaY = abs(y2 - y1);

int signX = x1 < x2 ? 1 : -1;

int signY = y1 < y2 ? 1 : -1;

int error = deltaX - deltaY;

for (;;)

{

setPixel(x1, y1);

if(x1 == x2 && y1 == y2)

break;

int error2 = error * 2;

if(error2 > -deltaY)

{

error -= deltaY;

x1 += signX;

}

if(error2 < deltaX)

{

error += deltaX;

y1 += signY;

}

}

}

Реализация на Java:

// Этот код "рисует" все 9 видов отрезков. Наклонные (из начала в конец и из конца в начало каждый), вертикальный и горизонтальный - тоже из начала в конец и из конца в начало, и точку.

private int sign (int x) {

return (x > 0) ? 1 : (x < 0) ? -1 : 0;

//возвращает 0, если аргумент (x) равен нулю; -1, если x < 0 и 1, если x > 0.

}

public void drawBresenhamLine (int xstart, int ystart, int xend, int yend, Graphics g)

/**

* xstart, ystart - начало;

* xend, yend - конец;

* "g.drawLine (x, y, x, y);" используем в качестве "setPixel (x, y);"

* Можно писать что-нибудь вроде g.fillRect (x, y, 1, 1);

*/

{

int x, y, dx, dy, incx, incy, pdx, pdy, es, el, err;

dx = xend - xstart;//проекция на ось икс

dy = yend - ystart;//проекция на ось игрек

incx = sign(dx);

/*

* Определяем, в какую сторону нужно будет сдвигаться. Если dx < 0, т.е. отрезок идёт

* справа налево по иксу, то incx будет равен -1.

* Это будет использоваться в цикле постороения.

*/

incy = sign(dy);

/*

* Аналогично. Если рисуем отрезок снизу вверх -

* это будет отрицательный сдвиг для y (иначе - положительный).

*/

if (dx < 0) dx = -dx;//далее мы будем сравнивать: "if (dx < dy)"

if (dy < 0) dy = -dy;//поэтому необходимо сделать dx = |dx|; dy = |dy|

//эти две строчки можно записать и так: dx = Math.abs(dx); dy = Math.abs(dy);

if (dx > dy)

//определяем наклон отрезка:

{

/*

* Если dx > dy, то значит отрезок "вытянут" вдоль оси икс, т.е. он скорее длинный, чем высокий.

* Значит в цикле нужно будет идти по икс (строчка el = dx;), значит "протягивать" прямую по иксу

* надо в соответствии с тем, слева направо и справа налево она идёт (pdx = incx;), при этом

* по y сдвиг такой отсутствует.

*/

pdx = incx; pdy = 0;

es = dy; el = dx;

}

else//случай, когда прямая скорее "высокая", чем длинная, т.е. вытянута по оси y

{

pdx = 0; pdy = incy;

es = dx; el = dy;//тогда в цикле будем двигаться по y

}

x = xstart;

y = ystart;

err = el/2;

g.drawLine (x, y, x, y);//ставим первую точку

//все последующие точки возможно надо сдвигать, поэтому первую ставим вне цикла

for (int t = 0; t < el; t++)//идём по всем точкам, начиная со второй и до последней

{

err -= es;

if (err < 0)

{

err += el;

x += incx;//сдвинуть прямую (сместить вверх или вниз, если цикл проходит по иксам)

y += incy;//или сместить влево-вправо, если цикл проходит по y

}

else

{

x += pdx;//продолжить тянуть прямую дальше, т.е. сдвинуть влево или вправо, если

y += pdy;//цикл идёт по иксу; сдвинуть вверх или вниз, если по y

}

g.drawLine (x, y, x, y);

}

}

10. Фрактал – математическое понятие, обозначающее абстрактный образ, построенный по принципу самоподобия с помощью алгебраических уравнений. Программа по заданным уравнениям рассчитывает значения, приводит их к форме, пригодной для отображения на экране в определенном цвете, и затем рисует по ним изображение. Чтобы построить по математическому выражению графическое изображение, программа рассчитывает много значений х и у, а затем в определяемых ими точках экрана ставит точки или рисует линии. Ниже подробно рассматривается построение всех трех фракталов.

Фрактал Kam Torus Фрактал Kam Torus рисует последовательность торов -поверхностей 1-го порядка, имеющих в трехмерном пространстве форму бублика, однако в нашем двухмерном случае, представляющий собой подобие эллипса. График Kam Torus порождается наложением рядов точек в некоторой орбите, генерируемых набором уравнений, в которых переменная на каждом шаге увеличивается на единицу. Три уравнения, управляющие рисованием имеют следующий вид: x(0) = y(0) = orbit / 3 x(n+1) = x(n)*cos(a) + (x² - y(n))*sin(a) y(n+1) = x(n)*sin(a) + (x² - y(n))*cos(a) После каждого прохода цикла значение orbit получает некоторое фиксированное приращение. Параметры, задающие поведение функции, включают в себя угол а (в радианах), величину шага для переменной orbit, конечное значение этой переменной и количество точек на орбиту, задающее число проходов цикла. При каждом запуске программы (или при каждой перерисовке содержимого окна) графики, построенные процедурой DrawKamTorus(), будут меняться, поскольку для создания начальных значений уравнений используются случайные числа.

Множество Джулии В отличие от фрактала Kam Torus, фрактал множество Джулии (как и рассматриваемый ниже множество Мандельброта) не использует генератор случайных чисел. Это множество порождает свой фрактал исходя из известных начальных значений. Множество Джулии может быть генерировано путем изменения в процессе описания множества Мандельброта. Для описания множества Джулии нужно начать с заданного значения C, комплексного числа (в форме a + (b * i)). Начальное значение Z также соответствует такому комплексному числу. Действительная часть данного числа соответствует координате x, а мнимая координате y, умноженной на i (мнимую единицу). Чтобы нарисовать фрактал, нужно последовательно применить уравнение Z(n+1) = Z(n)^2 + C для каждого из значений Z из ряда (0,…,n). Для каждой точки комплексной плоскости существует свое множество Джулии, то есть существует бесконечное число различных множеств Джулии. Но наиболее интересны визуально бувают полученные из таких значений C, для которых образ М-множества (т.е. родственного точечного множества Мандельброта) наиболее плотен.

Множество Мандельброта Фракталы, определяемые множеством Мандельброта, являются самыми известными и "знаменитыми". Это множество, как и множество Джулии рисует фрактал по его уравнению, используя комплексные числа и предопределенные отправные точки. Несмотря на известность и всеобщее признание, множество Мандельброта остается просто графиком: горизонтальная (х) и вертикальная (у) координаты представляют области изменения двух независимых величин. В двумерном представлении для передачи различных уровней третьей величины, зависящих от двух первых, используют цвет. Так же, как и во множестве Джулии, ось х опять представляет действительные числа, а ось у - мнимые. Итак, фрактал начинается от любой точки комплексной плоскости - C, комплексной константы. Затем берется другое комплексное число, которое уже может меняться - Z. Чтобы построить фрактал, следует начать с Z = 0 и вычислять выражение фрактала следующим образом: Z(n) = plot Z(n+1) = Z^2 + C В этом выражении производится итерация функции Z(n+1) = Z(n)^2 + C. Для некоторых значений С результат через некоторое время "выравнивается". Для остальных он беспредельно растет.

29