5) Динамика вращательного движения

Основной закон динамики вращательного движения:

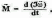
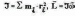или M=J , где М  момент силы M=[ r  F ] , J  момент инерции •момент импульса тела.

^-

если М(внешн)=0 - закон сохранения момента импульса. - кинетическая энергия вращающегося тела.

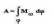работа при вращательном движении.

Теорема Штейнера. Момент инерции тела относительно произвольной оси J

где J₀ - момент инерции этого тела относительно оси, проходящей через центр тяжести тела параллельно заданной оси,

d - расстояние между осями,

m - масса тела.

Задачи для самостоятельного решения

17. (3.2) Два маленьких шарика массой m = 10 г каждый скреплены тонким невесомым стержнем длиной L = 20 см. Определить момент инерции J системы относительно оси, перпендикулярной стержню и проходящей через центр масс.

(J= 2-10^-4 кг·м²)

18. (3.21) Тонкий однородный стержень длиной L = 50 см и массой m = 400 г. вращается с угловым ускорением ε = 3 рад/с², около оси, проходящей перпендикулярно стержню через его середину. Определить вращающий момент

( 0, 025 Н-м ).

19. (3.25) Через блок, имеющий форму диска, перекинут шнур. К концам шнура привязали грузики массой m₁ = 100 г и m₂; = 110 г. С каким ускорением а будут двигаться грузики, если масса m блока равна 400 г ? Трение при вращении блока ничтожно мало.(0,24м/с²)

20. (3.28) Шар массой m=10кг и радиусом R=20см вращается вокруг оси, проходящей через его центр. Уравнение вращения шара имеет вид:

 = А + Bt²+Ct³, где В = 4 рад/с². С = -1 рад/с³.

Найти закон изменения момента сил, действующих на шар. Определить момент сил М в момент времени t = 2 с. (- 0,64 Н м ).

21. (3.41) Якорь мотора вращается с частотой n= 1500 мин^-1. Определить вращающий момент М, если мотор развивает мощность N = 500 вт.

(3,18 Нм).

22. (3.49) Обруч и сплошной цилиндр, имеющие одинаковую массу m = 2кг, катятся без скольжения с одинаковой скоростью V = 5 м/с. Найти

кинетические энергии W₁ и W₂; этих тел. (500ДЖ, 37,5 Дж).

23. (3.51) Определить линейную скорость v центра шара. скатившегося без скольжения с наклонной плоскости высотой h=1 м. (3,74 м/с).

24. (3.55) Карандаш длиной l=15 см, поставленный вертикально, падает на стол. Какую угловую  и линейную скорость V будет иметь в конце падения середина карандаша? Считать, что трение настолько велико, что нижний конец карандаша не проскальзывает.

(14 Рад/с, 2,1 м/с).

25°. Вращение от двигателя к ведущим колесам автомобиля передается через ряд устройств, одно из которых, называемое сцеплением, позволяет в случае надобности отключить двигатель от остальных устройств. Сцепление, в принципе, состоит из двух одинаковых фрикционных накладок, прижимаемых друг к другу сильными пружинами. В автомобиле "Жигули” фрикционные накладки имеют форму колец с внутренним диаметром d₁ = 142 мм и наружным диаметром d₂ =203 мм. Коэффициент трения прокладки по прокладке  = 0,35. Най­ти наименьшую силу F, с которой нужно прижимать накладки, чтобы передавать вращательный момент М=100Нм.

26*.

Н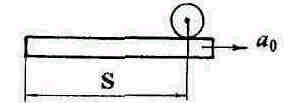 а шероховатой доске на расстоянии S от её левого конца находится сплошной цилиндр. Доску начинают двигать с ускорением a₀ вправо. С какой скоростью относительно доски будет двигаться центр инерции цилиндра

в тот момент, когда он будет находиться над краем доски? Движение цилиндра относительно доски происходит без скольжения.

Момент инерции

        величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. В механике различают М. и. осевые и центробежные. Осевым М. и. тела относительно оси z называется величина, определяемая равенством:

         

        где m_i — массы точек тела, h_i — их расстояния от оси z, ρ — массовая плотность, V — объём тела. Величина I_z является мерой инертности тела при его вращении вокруг оси (см.Вращательное движение). Осевой М. и. можно также выразить через линейную величину k, называемую радиусом инерции, по формуле I_z = Mk², где М — масса тела. Размерность М. и. —L²M; единицы измерения — кг․м² или г․см².

         Центробежным М. и. относительно системы прямоугольных осей х, у, z, проведённых в точке О, называют величины, определяемые равенствами:

         

        или же соответствующими объёмными интегралами. Эти величины являются характеристиками динамической неуравновешенности масс. Например, при вращении тела вокруг оси z от значений I_xz и I_yz зависят силы давления на подшипники, в которых закреплена ось.

         М. и. относительно параллельных осей z и z' связаны соотношением

         I_z = I_z' + М d² (3)

        где z' — ось, проходящая через центр масс тела, a d — расстояние между осями (теорема Гюйгенса).

         М. и. относительно любой, проходящей через начало координат О оси Ol с направляющими косинусами α, β, γ находится по формуле:

         l_ol = I_x α² + I_y β² + I_z γ² — 2I_xy αβ — 2I_yz βγ — 2I_zxγα. (4)

        Зная шесть величин I_x, I_y, I_z, I_xy, I_yх, I_zx, можно последовательно, используя формулы (4) и (3), вычислить всю совокупность М. и. тела относительно любых осей. Эти шесть величин определяют т. н. тензор инерции тела. Через каждую точку тела можно провести 3 такие взаимно-перпендикулярные оси, называемые главными осями инерции, для которых I_xy = I_yz =I_zx = 0. Тогда М. и. тела относительно любой оси можно определить, зная главные оси инерции и М. и. относительно этих осей.

         М. и. тел сложной конфигурации обычно определяют экспериментально. Понятием о М. и. широко пользуются при решении многих задач механики и техники.