§ 4.3. Корреляційний аналіз

Попередній аналіз тісноти взаємозв'язку параметрів багатовимірної моделі здійснюється по оцінці корреляційної матриці генеральної сукупності X за спостереженнями. Для цього використовується інструмент Аналіз даних у відповідності з наступним алгоритмом :

• розмістити на робочому аркуші Excel статистичні дані в стовпцях з відповідними заголовками (іменами змінних );

• Сервіс – Аналіз даних – Корреляція ;

• у діалоговому вікні Корреляція, що з'явилося, у відповідні поля ввести за допомогою миші вхідні дані й параметри виводу (див.рис. 3 ) ;

• після щиглика мишею по кнопці OK на робочому аркуші з'явиться матриця, що містить оцінки парних коефіцієнтів корреляції.

• Відібрати для подальшого аналізу пари змінних, що мають найбільші значення парних коефіцієнтів корреляції

( 0,4 ), з огляду на те, що чим менше коефіцієнт r_ij , тим слабкіше їхній зв'язок. Такими парами в наведеному прикладі (рис.3) є: Y2-X4; Y2-X8; X4-X6; X5-X7; X7-X8. Причому ознака X4 зв'язана з усіма іншими компонентами з від’ємним коефіцієнтом корреляції. Це говорить про зворотну залежність, що цілком природно для трудомісткості одиниці продукції й інших показників.

• Перевірити значимість коефіцієнтів корреляції на рівні 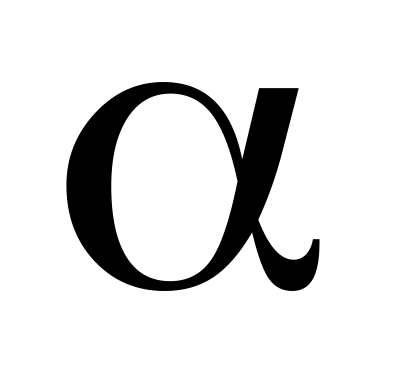= 0,05. Оскільки обсяг вибірки для всіх ознак однаковий і дорівнює 53, критичне значення r_кр для всіх пар буде однаковим й відповідно до таблиці Фішера–Йєтса r_кр = r_табл (0,05;53)< r_табл(0,05;50) = 0,273. Оскільки для всіх коефіцієнтів виконується нерівність > r_кр , коефіцієнти корреляції всіх відібраних пар ознак значимо відрізняються від нуля, що підтверджує зв'язок між ними.

Подальший аналіз статистичних даних залежить від розмірності прийнятої моделі. Найпростіший варіант – двовимірна модель. З огляду на те, що в наведеному прикладі Y2 - результативна ознака, що визначає індекс зниження собівартості продукції, входить у дві пари , треба розглянути тривимірну модель Y2–X4–X8, де X4 -трудомісткість одиниці продукції, а X8 – премії й винагороди на одного працівника. В інших парах треба визначити залежності між X6 й X4, X7 й X8 , X5 й X7. Тут X5 -питома вага робітників у складі промислово-виробничого персоналу, X6 – питома вага покупних виробів, X7 – коефіцієнт змінності устаткування.

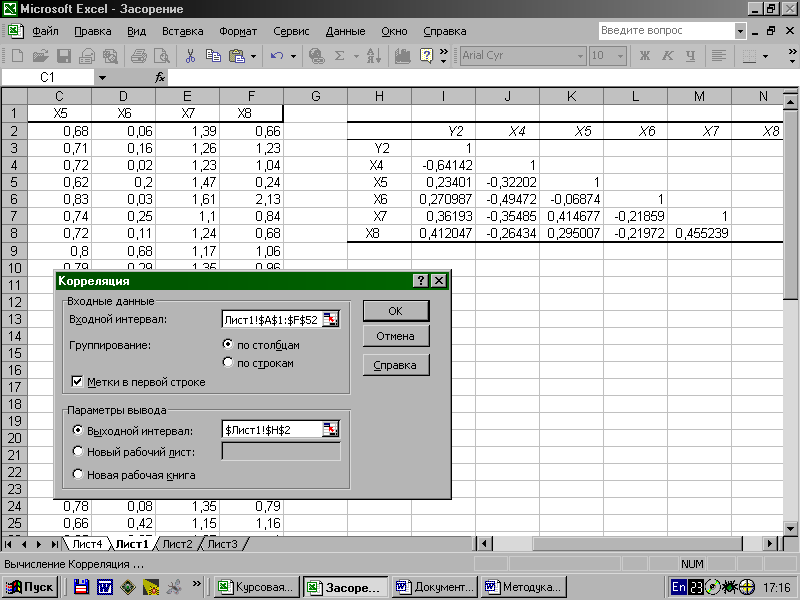
Рис.3.Аналіз парної корреляції.

Таким чином, для математичної моделі задачі вибору оптимального управління діяльністю підприємства з урахуванням зазначених показників треба встановити залежності :

Y2 = F( X4,X8) - цільова функція;

X6 = φ(X4); X8 = φ(X7); X5 = φ(X7) - обмеження.

§4.4. Регресійний аналіз двовимірної моделі.

У середовищі Excel для двовимірного випадку лінійної регресії передбачено кілька інструментів : статистичні функції (КОРРЕЛ, ЛИНЕЙН, ТЕНДЕНЦІЯ й ін.) ; інструмент Регресія надбудови Пакет аналізу ; графічні засоби при роботі з діаграмою – побудова лінії тренда.

За допомогою Пакета аналізу можна одержати шукану інформацію , дотримуючись такого алгоритму :

• розмістити на робочому аркуші Excel у двох суміжних стовпцях з відповідними заголовками статистичні дані по двох ознаках, що підлягають дослідженню (наприклад, X4 й X6);

• Сервіс – Аналіз даних – Регресія ;

• у діалоговому вікні Регресія, що з'явилося, ввести вхідні дані в поля Вхідний інтервал Y (X6) і Вхідний інтервал X (X4) і клацнути по полю Мітки , щоб заголовки не ввійшли в інтервали даних;

• ввести параметри виводу в поле Вихідний інтервал адресу лівого верхнього кута таблиці результатів або клацнути поле Новий робочий аркуш для виводу на інший аркуш (див.рис. 4);

• для наочності можна вивести графік , клацнувши по полю Графік підбора ;

• OK.

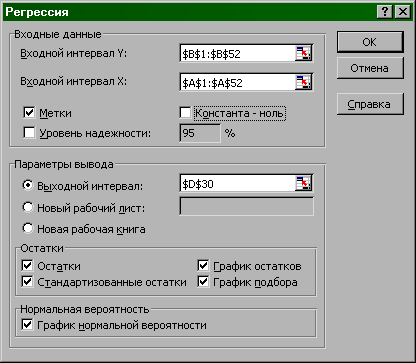
Рис.4.Робота з діалоговим вікном Регресія.

Результат роботи інструмента Регресія наведено на рис. 5. Отже, вибіркове рівняння лінійної регресії X6 на X4 має вигляд :

Вихідна таблиця містить коефіцієнт детермінації R² = 0,368802, що означає, що отримана модель приблизно на 37% відбиває залежність питомої ваги покупних виробів від трудомісткості одиниці продукції.

Стандартна похибка (відхилення результату) = 0,118415 означає, що 68% реальних значень результуючої ознаки x₆ перебуває в діапазоні 0,118415 від лінії регресії. Це випливає з того, що умовні розподіли нормально розподіленої генеральної сукупності при фіксуванні різних підмножин компонент є нормальними.

У розділі Дисперсійний аналіз наведені значення таких величин :

df – число ступенів волі ; SS -сума квадратів відхилень ; MS – дисперсія ; F – розрахункове значення F-критерію. Оскільки критичне значення критерію Фішера F_кр = 4,03 (m₁=1; m₂=50; ), F_расч =28,63 > F_кр , і, отже з імовірністю гіпотеза про відсутність зв'язку між розглянутими ознаками відкидається. Це означає, що рівняння в цілому статистично значиме, тобто добре відповідає даним спостережень.

ВИВІД ПІДСУМКІВ
Регресійна статистика
Множинний R	0,607291
R-квадрат	0,368802
Нормований R-квадрат	0,35592
Стандартна помилка	0,118415
Спостереження	51
Дисперсійний аналіз
	df		SS	MS	F	Значимість F
Регресія	1		0,401452	0,401452	28,63014	2,3E-06
Залишок	49		0,687078	0,014022
Разом	50		1,088529
	Коефіцієнти		Стандартна похибка	t-статистика	P-Значення	Нижні 95%	Верхні 95%
Y-перетинання	0,557512		0,051111	10,90789	1,04E-14	0,45480	0,66022
X4	-0,85062		0,158973	-5,35071	2,3E-06	-1,1701	-0,5312

Рис.5. Результати регресійного аналізу .

Нижня частина таблиці містить такі відомості :

Коефіцієнти – оцінки параметрів рівняння регресії;

Стандартна похибка – стандартні відхилення ;

t-статистика – розрахункове значення . Таким чином, можна оцінити значимість коефіцієнтів рівняння регресії, зрівнявши розрахункове значення t – статистики із критичним значенням, знайденим по розподілу Стьюдента при рівні значимості й m=50 : t_кр =2,009 . Оскільки > t_кр для обох коефіцієнтів , то вони є статистично значимими при рівні довірчої ймовірності 0,95 .

Нижні 95% і Верхні 95% визначають нижні й верхні границі довірчих інтервалів для коефіцієнтів рівняння регресії при . Оскільки довірчі інтервали не містять 0 , це підтверджує значимість коефіцієнтів рівняння регресії.

X4	X6
0,01	0,35
0,02	0,42
0,17	0,5
0,17	0,53
0,18	0,68
0,18	0,32
0,19	0,4
0,22	0,54
0,23	0,4
0,23	0,42
0,23	0,47
0,23	0,4
0,24	0,56
0,24	0,26
0,25	0,2
0,25	0,33
0,26	0,44
0,26	0,3
0,26	0,27
0,27	0,37
0,29	0,4

Рис. 6. Лінії тренда.

Для здобуття лінії регресії і її рівнянь у випадку двовимірної моделі зручним інструментом Excel є додавання лінії тренда до точкової діаграми, побудованої на значеннях компонентів системи двох заданих випадкових величин як результатів спостереження (див. рис. 6).

Алгоритм містить такі дії :

• розмістити на робочому аркуші Excel у двох суміжних стовпцях вихідні дані таким чином, щоб першим був незалежний показник;

• Вставка – Діаграма – Точкова (перший варіант) – Далі ;

• на закладці Діапазон даних увести діапазон , займаний всією таблицею, для чого виділити мишею обидва стовпці ;

• на закладці Ряд увести в поле Значення X діапазон значень незалежної величини , а в поле Значення Y діапазон значень величини, регресію якої треба оцінити (див. рис. 7 );

• Далі – на закладці Заголовки ввести заголовки осей і діаграми – Далі – указати , де розмістити діаграму (на наявному аркуші ) – Готово;

• відкоригувати діаграму, що з'явилася, особливо формат осей і написи, для чого клацнути правою кнопкою миші по осі або напису й у маленькому діалоговому вікні, що з'явилося, клацнути по пункту Формат осі (або напису) ;

• в діалоговому вікні Формат осі (або напису ), що з'явилося, вибрати потрібну закладку й внести необхідні зміни - OK ;

• відкоригувати отримане корреляційне поле, виключивши окремі точки, що різко виділяються із загальної множини;

• клацнути правою кнопкою миші по будь-якій точці діаграми й у діалоговому вікні, що з'явилося, вибрати пункт меню Додати лінію тренда;

• в діалоговому вікні, що з'явилося, на закладці Тип вибрати тип залежності : лінійний або поліноміальний ( указати порядок наближення ) ;

• клацнути по закладці Параметри й у діалоговому вікні послу, що з'явилося після цього, клацнути пункти показувати рівняння на діаграмі й помістити на діаграму величину вірогідності апроксимації (R^2) ;

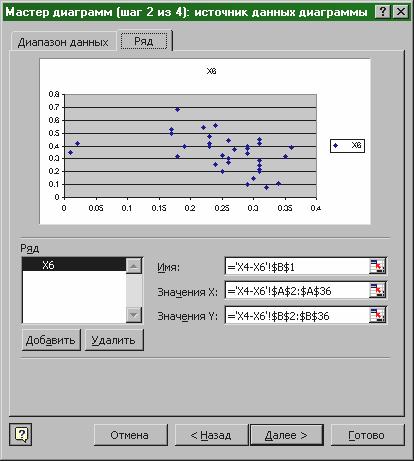
Рис.7. Побудова кореляційного поля.

• записати рівняння регресії , замінивши y та x на імена результативної й факторної ознак відповідно й оцінити значимість отриманого рівняння за допомогою R^2.

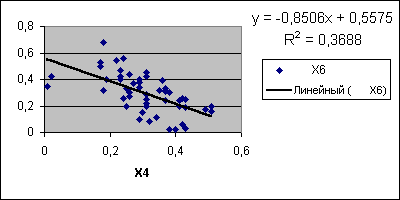
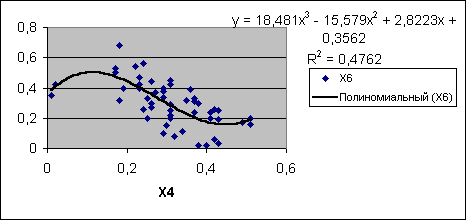
На рис.6 наведені: точкова діаграма залежності X6 від X4 і дві лінії тренда – лінійна й нелінійна. Рівняння першої збігається з рівнянням лінійної регресії , отриманим за допомогою інструмента Регресія . Друга має рівняння , тобто оцінку лінії регресії, такого виду :

.

Причому коефіцієнт детермінації в першому випадку дорівнює 0,3688 , а для кубічної залежності R² = 0,4762 , тобто слід використати поліноміальну залежність як таку, що краще погоджується зі статистичними даними.

Для інших двох відібраних пар факторних ознак необхідно виконати такі ж дії й одержати аналогічні оцінки функцій регресії.