Учебные задачи и диагностируемые цели темы

Учебные задачи: формирование у учащихся новых методов решения задач: метод разбиения и дополнения, алгебраический метод.

Основное понятие темы – понятие площади многоугольника.

Диагностируемые цели:

В результате изучения темы ученик

• Знает:

• понятие площади многоугольника;

• различные единицы измерения площади;

• основные свойства площадей;

• формулы площади квадрата, прямоугольника;

• Умеет:

• переводить из одной единицы измерения площади в другую;

• доказывать теорему о площади прямоугольника;

• применять формулы для вычисления площади квадрата и прямоугольника;

• применять метод разбиения и дополнения для решения задач;

• Понимает:

• аналогию между измерением длин отрезков и измерением площадей плоских фигур;

• из чего состоит процесс измерения площади плоской фигуры;

• на чём основано доказательство теоремы о площади прямоугольника.

2 Балла Конспект урока по теме: Площадь многоугольника

Геометрия: Учеб. для 7-9 кл. сред. шк. /Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. – 3-е изд. М. : Просвещение, 1992

Стр. 114 – 120, глава 6, §1

Тип урока: урок изучения нового.

Учебная задача урока: в совместной деятельности с учащимися ввести понятие площади многоугольника, единицы измерения площади, процесса измерения площади многоугольника по аналогии с процессом измерения длины отрезка, рассмотреть свойства площадей, формулы площади квадрата и прямоугольника, доказать теорему о площади прямоугольника.

Диагностируемые цели:

В результате урока ученик

• Знает:

• понятие площади многоугольника;

• различные единицы измерения площади;

• основные свойства площадей;

• формулы площади квадрата и прямоугольника;

• Умеет:

• переводить из одной единицы измерения площади в другую;

• доказывать теорему о площади прямоугольника;

• применять формулы для вычисления площади квадрата и прямоугольника;

• применять метод разбиения и дополнения для решения задач;

• Понимает:

• аналогию между измерением длин отрезков и измерением площадей плоских фигур;

• из чего состоит процесс измерения площади плоской фигуры;

• на чём основано доказательство теоремы о площади прямоугольника.

Методы обучения: эвристическая беседа, частично-поисковые, репродуктивный.

Форма работы: фронтальная.

Средства обучения: мел, доска, учебник, канва-таблица, модели плоских фигур, палетка.

Ученикам предварительно дается задание повторить дома понятие длины отрезка и ее свойства (глава 1, §4 «Измерение отрезков», стр. 13-15).

Структура урока:

1. Мотивационно-ориентировочный этап (10 минут)

2. Содержательный этап (30 минут)

3. Рефлексивно-оценочный этап (5 минут)

Ход урока:

1. Мотивационно-ориентировочный этап

1. Актуализация

Повторяется понятие длины отрезка и ее свойства.

1. Вспомним, решая следующие задачи, что такое длина отрезка и какие она имеет свойства. Раздается канва-таблицы.

	Длина отрезка
Что показывает?
Какая это величина?
Свойства
Обозначение
Единицы измерения

№1

Найдите длины всех отрезков, изображенных на рисунке, если за единицу измерения принят отрезок:

1. K 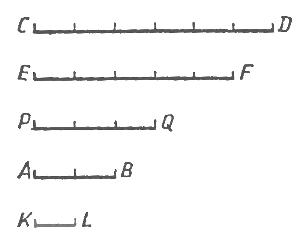L; (Ответ: a) CD=6KL; EF=5KL; PQ=3KL; AB=2KL;

2. AB; b)CD=3AB; EF=2,5AB; PQ=1,5AB; KL=0,5AB)

2. Что показывает длина отрезка? (Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

3. Какое по знаку это число? (Положительное число.)

Заполняются соответствующие строки в канве таблице.

№2

1. П

   A

   В

   O

   остройте произвольный отрезок AB. Разделите его пополам. Обозначим середину отрезка точкой O. Измерьте отрезки AO и OB, сравните их длины.

Длины отрезков АО и ОВ равны.

Получили 1 свойство длины отрезка: Равные отрезки имеют равные длины.

2. Начертите отрезок АВ, между точками А и В поставьте точки С и D, что получилось? Измерьте получившиеся отрезки, найдите их сумму, измерьте АВ. Что получили?

AC=6 см;

CD=2 см;

BD=1 см;

AC+CD+BD=9 см;

AB=9 см.

(2 свойство: Если отрезок разделен на несколько отрезков, то длина этого отрезка равна сумме длин отрезков, составляющих его.)

Заполняются соответствующие строки в канве таблице.

4. Повторим, решая задачу №3, перевод величин:

№3

Перевести:

1. 5,8 м в см;

2. 5 дм 1 см в см;

3. 3,3 км 300 м в м.

Решение:

1. 5,8 м = 580 см;

2. 5 дм 1 см = 51 см;

3. 3,3 км 300 м = 3600 м.

Заполняются соответствующие строки в канве таблице.

2. М отивация

Вычислите площадь квадрата BPTF, если известно, что сторона AB = 3 см, а сторона BD =5 см. APQC и DCEF – квадраты, a ABDC и CQTE - прямоугольники. (64 см²)

Решение:

1. ABDC – прямоугольник; ;

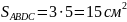2. APQC – квадрат, BD=AC=5 см; ;

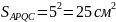3. DCEF – квадрат; AB=CD=3 см; ;

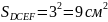4. CQTE – прямоугольник; ;

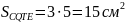5. Можно предположить, что площадь большого квадрата равна сумме площадей фигур APQC, DCEF, ABDC, CQTE. Тогда .

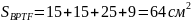Сейчас вы пользовались формулами для вычисления площадей квадрата и прямоугольника. Назовите их. ( ; )

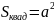С понятием площади все знакомы из повседневной жизни, каждый понимает, что такое площадь комнаты, квартиры, садового участка.

Измерять площадь научились еще в Древнем Вавилоне. Вавилоняне измеряли простейшие фигуры, связанные с практическими нуждами – измерение и межевание земель, строительство плотин и каналов, возведение стен и т. д. Сохранилось немало планов земельных угодий, разделенных на прямоугольники, трапеции и треугольники, а также планов различных строений, свидетельствующих, что вавилонский землемер или архитектор должен был хорошо чертить и проводить геометрические расчеты.

3. Постановка учебной задачи урока.

Тема нашего урока – “Площадь многоугольника”. Учащиеся записывают тему урока в тетрадь и в соответствующую строку в канве-таблице.

Сформулируйте цели урока.

• Рассмотреть подробнее понятие площади и ее свойства.

• Изучить теорему о площади прямоугольника и ее доказательство.

• Углубить навык решения задач по данной теме.