
- •Понятие множества. Примеры множеств. Способы задания множеств.
- •Пустое множество. Равные множества. Подмножества. Примеры.
- •Универсальное множество. Дополнение множества до универсального множества.
- •Кортеж. Декартово умножение множеств.
- •Отношения эквивалентности и порядка.
- •Отображения. Функции. Равномощные множества. Композиция отображений.
- •12.Мощность множества. Счетные множества. Мощность континуума.
- •14.Понятие перестановки. Число перестановок n-элементного множества.
- •16. Понятия размещения. Числа всех размещений из n элементов по k элементов.
- •17. Треугольник паскаля и его свойства. Бином ньютона, его свойства и некоторые приложения.
- •18. Метод рекуррентных соотношений (определение и примеры).
- •Решение рекуррентных соотношений. Примеры.
- •21. Линейные рекуррентные соотношения с постоянными коэффициентами.
- •Числа Фибоначчи, их свойства и приложения.
- •23.. Числа Каталана. Числа Стирлинга (1-го и 2-го рода), гармонические числа.
- •25. Производящие функции.
- •Целочисленные функции округления.
- •27.Иерархия.Асимптотическая аппроксимация.
- •29.Графы, ориентированные графы, псевдографы, мультиграфы.
- •31.Маршруты, пути.
- •32.Матричное задание графов.
- •33.Операции над графами, подграфы.
- •35. Поиск маршрутов в графах.
- •36.Деревья, свойства деревьев. Лес.
- •38.Эйлеровы графы и циклы.
- •40.Планарные графы.
- •41.Правильная раскраска вершин графов.
- •43.Принцип Дирихле.
- •45.Приложение теоремы Рамсея. Теорема Ван дер Вардена.
- •46.Двудольные графы. Теорема Кенига
25. Производящие функции.
Пусть ![]() —
произвольная (бесконечная) последовательность
чисел (целых, рациональных, вещественных
или комплексных). Производящей
функцией (производящим рядом) называется
запись вида
—
произвольная (бесконечная) последовательность
чисел (целых, рациональных, вещественных
или комплексных). Производящей
функцией (производящим рядом) называется
запись вида
![]() Замечание. Не
следует думать, что мы можем сказать,
чему равно значение производящей
функции
Замечание. Не
следует думать, что мы можем сказать,
чему равно значение производящей
функции ![]() в
точке
в
точке ![]() .
Переменная
.
Переменная ![]() является
формальной, и ряд
является
формальной, и ряд ![]() смысла
не имеет. Единственное, что мы можем
сказать про функцию
смысла
не имеет. Единственное, что мы можем
сказать про функцию ![]() ,
это что ее значение в нуле равно
,
это что ее значение в нуле равно ![]() .
Если, однако, производящий ряд является
полиномом (т.е. все его коэффициенты
кроме конечного числа равны нулю), то
значение этого ряда в любой точке
выражается конечной суммой и поэтому
имеет смысл.
.
Если, однако, производящий ряд является
полиномом (т.е. все его коэффициенты
кроме конечного числа равны нулю), то
значение этого ряда в любой точке
выражается конечной суммой и поэтому
имеет смысл.
Целочисленные функции округления.
27.Иерархия.Асимптотическая аппроксимация.
28.Формула суммирования Эйлера-Маклорена.
формула суммирования, связывающая частные суммы ряда с интегралом и производными его общего члена:
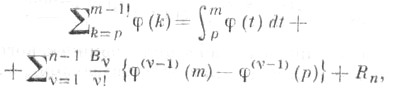 где
где ![]() - Бернулли
числа, Rn - остаточный
член. С помощью Бернулли
многочленов Bn(t),
В n(0)=В п остаточный
член записывается в виде:
- Бернулли
числа, Rn - остаточный
член. С помощью Бернулли
многочленов Bn(t),
В n(0)=В п остаточный
член записывается в виде:
![]() Для n=2sостаточный
член R2s может
быть представлен с использованием
чисел Бернулли:
Для n=2sостаточный
член R2s может
быть представлен с использованием
чисел Бернулли:
![]() Если
производные
Если
производные ![]() и
и ![]() имеют
одинаковые знаки и не меняют знака на
[ р,
т],то
имеют
одинаковые знаки и не меняют знака на
[ р,
т],то
![]() Э.-М.
ф. играет важную роль при изучении
асимптотич. разложений, в теоретико-числовых
оценках, в конечных
разностей исчислении. Э.-М.
ф. была впервые приведена Л. Эйлером
[1] в виде:
Э.-М.
ф. играет важную роль при изучении
асимптотич. разложений, в теоретико-числовых
оценках, в конечных
разностей исчислении. Э.-М.
ф. была впервые приведена Л. Эйлером
[1] в виде:
![]() где S
- сумма
первых членов ряда с общим членом t(п),
S=t=0
при n=0,
а коэффициенты определяются рекуррентными
соотношениями:
где S
- сумма
первых членов ряда с общим членом t(п),
S=t=0
при n=0,
а коэффициенты определяются рекуррентными
соотношениями:
![]() Независимо
формула была открыта позднее К.
Маклореном.
Независимо
формула была открыта позднее К.
Маклореном.
29.Графы, ориентированные графы, псевдографы, мультиграфы.
Графом G(V,E) называется совокупность двух множеств — непустого множества V (множества вершин) и множества Е двухэлементных подмножеств множества V (Е — множество рёбер). G(V, E) = (V;E), V^0, Е С 2V кVe G E |e| = 2. Если элементами множества Е являются упорядоченные пары (то есть Е с V х V), то граф называется ориентированным (или орграфом). В этом случае элементы множества V называются узлами, а элементы множества Е — дугами. Если элементом множества Е может быть пара одинаковых (не различных) элементов V, то такой элемент множества Е называется петлей, а граф называется графом с петлями (или псевдографом). Если Е является не множеством, а набором, содержащим несколько одинаковых элементов, то эти элементы называются кратными ребрами, а граф называется мультиграфом.
30.Изоморфизм
и гомеоморфизм графов, двудольные
графы.Говорят,
что два графа G\1V1,Ei) и G2(V2,E2) изоморфны
(обозначается G1 ~ G2), если существует
биекция h: V1—► V2, сохраняющая смежность
ei = (u,v) е Ех <=> е2 = (h(u),h(v)) e E2. Пусть А
= (-А, fi, П) и В = (В, П, П) — две однотипные
алгебраические системы. Отображение
h: А-± В называют гомоморфизмом
алгебраической системы А в алгебраическую
систему В, если выполняются следующие
условия: 1) для любой п-арной операции
ш (![]() )
и любых элементов
)
и любых элементов
![]() 2)
для любого п-арного отношения тг (n ^ 1)
и любых элеэлементов
2)
для любого п-арного отношения тг (n ^ 1)
и любых элеэлементов
![]() следует
следует
![]() Двудольный
граф (или биграф, или чётный граф) — это
граф G(V, E)y такой что множество V разбито
на два непересекающихся множества V1 и
V2 (Vi U V2 = V2 &V1 П V2 = 0), причем всякое ребро
из Е инцидентно вершине из V1 и вершине
из V2 (то есть соединяет вершину из Vi с
вершиной из V2). Множества V1 и V2 называются
долями двудольного графа. Если двудольный
граф содержит
Двудольный
граф (или биграф, или чётный граф) — это
граф G(V, E)y такой что множество V разбито
на два непересекающихся множества V1 и
V2 (Vi U V2 = V2 &V1 П V2 = 0), причем всякое ребро
из Е инцидентно вершине из V1 и вершине
из V2 (то есть соединяет вершину из Vi с
вершиной из V2). Множества V1 и V2 называются
долями двудольного графа. Если двудольный
граф содержит
все рёбра, соединяющие множества V\ и V2l то он называется полным двудольным графом..
