5.Связь между линейными и угловыми характеристиками вращательного движения твердого тела.

расстоянии r , то за время dt она проходит путь 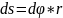Скорость точк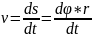и , или

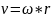
При вращении тела тангенциальное ускорение его точки , или

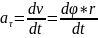
Нормальное ускорение точки тела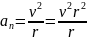 , или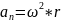 Полное ускорение, как указывалось ранее, определяют по формуле

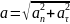
6.Плоское движение твердого тела. Мгновенная ось вращения. Динамика плоского движения.

Плоским или плоскопараллельным движением твердого тела называется такое его движение, при котором каждая точка тела движется в плоскости, параллельной некоторой неподвижной плоскости, например движение колеса вагона на прямолинейном участке пути, движение шатуна кривошипно-шатунного механизма. Рассмотрим движение плоской фигуры, представляющей собой сечение тела, находящегося в плоском движении, плоскость 2 , параллельной неподвижной плоскости 1 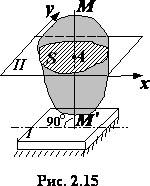При плоском движении все точки тела, лежащие на прямой MM’ , перпендикулярной к сечению S , т. е. к плоскости I , движутся тождественно. Поэтому вместо плоского движения тела достаточно изучить движение плоской фигуры в ее плоскости.В кинематике твердого тела изучаются три основных вопроса: задание движения тела, вычисление скорости какой-либо его точки и вычисление ее ускорения. Кроме этих вопросов изучаются и другие вопросы, представляющие научный и технический интерес. Положение движущейся плоской фигуры в ее плоскости относительно неподвижной системы осей координат Oxy определяется положением какого-либо отрезка, жестко связанного с этой фигурой 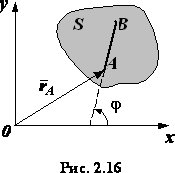Положение отрезка AB можно определить, зная радиус-вектор rA точки A и угол , который образует отрезок AB с осью Ox. Точку называют полюсом. При движении тела величины и будут изменяться в зависимости от времени, т. е. rA=rA(t) - называются уравнениями плоского движения твердого тела. Теорема. Всякое перемещение плоской фигуры в ее плоскости можно представить как совокупность двух перемещений: 1) поступательного перемещения, зависящего от выбора полюса; 2) вращательного перемещения вокруг полюса; угол и направление поворота от выбора полюса не зависят. Доказательство. Пусть в момент времени t фигура занимала положение I 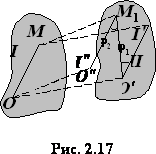а в момент времени t+∆t – положение 2 . Переместим сначала фигуру поступательно в положение I’ а затем повернем ее на угол 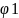вокруг точки O’ . Заметим, что поступательное перемещение зависит от выбора полюса, а угол поворота не зависит от него. Действительно, тот же переход из положения I в положение I’ можно осуществить, приняв за полюс точку и переместив сначала фигуру в положение I’ (причем все точки фигуры получат перемещения, геометрически равные MM’ и отличные от OO’ , а затем повернув фигуру на угол O’M1O’= вокруг точки M1. так как отрезки O’M’ и O’M параллельны и повороты вокруг точек O’ и M’ происходят в одну сторону. Продифференцировав равенство, получим 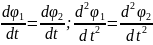т. е. угловая скорость и угловое ускорение не зависят от выбора полюса плоской фигуры при плоском ее движении.ОСЬ ВРАЩЕ́НИЯ, прямая, неподвижная относительно вращающегося вокруг нее твердого тела. Для твердого тела, имеющего неподвижную точку (напр., для детского волчка), прямая, проходящая через эту точку, поворотом вокруг которой тело перемещается из данного положения в положение, к нему бесконечно близкое, называется мгновенной осью вращения.МГНОВЕННАЯ ОСЬ ВРАЩЕНИЯ- прямая, неподвижная в данный момент в нек-рой инерциальной системе отсчёта, относительно к-рой сложное движение твёрдого тела в этот момент можно представить как вращат. вокруг этой прямой. М. о. в. может лежать как внутри тела, так и вне его. С течением времени положение М. о. в. изменяется относительно как неподвижной системы отсчёта, так и системы отсчёта, движущейся вместе с телом. При равномерном или неравномерном вращении твердого тела вокруг постоянной неподвижной оси все точки тела, находящиеся на оси, остаются неподвижными; гораздо сложнее и разнообразнее вращательные движения твердого тела вокруг неподвижной точки, которая одна только остается в покое. Как бы ни было сложно такое движение, одновременные скорости всех точек тела имеют такие величины и направления, как будто бы тело вращалось вокруг некоторой оси, проходящей через неподвижную точку, так что скорости точек тела, находящихся на этой оси, равны нулю, а скорости прочих точек перпендикулярны к плоскостям, проходящим через них и через вышесказанную ось, и пропорциональны кратчайшим расстояниям от этой оси. Эта ось называется мгновенной осью вращения и величина отношений скоростей точек к кратчайшим расстояниям их от мгновенной оси — мгновенной угловой скоростью. Мгновенными называются они потому, что как направление оси, так и величина угловой скорости изменяются с течением времени. 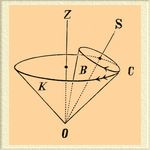В положении, изображенном на чертеже, мгновенной осью служит производящая OC обоих конусов; если качение происходит в таком направлении, что ось OS симметрии конуса B перемещается слева направо по отношению к оси симметрии OZ конуса K, то мгновенная ось (т. е. место прикосновения поверхностей) будет перемещаться в пространстве по поверхности конуса K в сторону, указанную двойной строкой, и по поверхности конуса B — в сторону, указанную простой стрелкой. Каково бы ни было вращение твердого тела вокруг неподвижной точки, если только это не есть вращение вокруг неподвижной постоянной оси, мгновенная ось вращения изменяет свое положение в пространстве и в теле. Коническая поверхность или пирамида, вычерчиваемая мгновенной осью в пространстве, называется неподвижным аксоидом, а коническая поверхность, вычерчиваемая ею в твердом теле — подвижным аксоидом