42.Связанные системы. Парциальные и нормальные колебания. Представление движения системы с помощью нормальных колебаний.

СВЯЗАННЫЕ СИСТЕМЫ- колебательные системы с двумя и более степенями свободы, рассматриваемые как совокупность систем с одной степенью свободы каждая (парциальных систем), взаимодействующих между собой. Два или неск. колебательных контуров у к-рых колебания в одном контуре из-за наличия связи вызывают колебания в других. Происходит переход энергии из одной системы в другую. Наличие связи изменяет характер резонансных явлений по сравнению с одиночным контуром. Резонанс наступает всякий раз, когда частота внеш. воздействия совпадает с одной из частот собственных колебаний всей системы, отличающихся от парциальных частот отд. контуров состоящей из двух контуров, резонанс наступает на двух разл. частотах.

43.Продольные и поперечные волны. Амплитуда, фаза, скорость распространения волы.

Длина волны - это расстояние между ближайшими точками, колеблющимися в одинаковых фазах. Величины, характеризующие волну:  длина волны, скорость волны, период колебаний, частота колебаний. Единицы измерения в системе СИ: длина волны [лямбда] = 1 м, скорость распространения волны [ v ] = 1м/с. период колебаний [ T ] = 1c. частота колебаний [ ню ] = 1 Гц Волны, рассматриваемый параметр которых изменяется периодически вдоль оси распространения, называются продольными волнами. Если колебания происходят перпендикулярно оси распространения волны (как у электромагнитных волн, например), то такие волны называются поперечными. В поперечной волне колебания происходят в направлении, перпендикулярном направлению распространения волны. Как и в случае продольных волн амплитуды колебаний всех шариков одинаковы, а фаза линейно изменяется от шарика к шарику y₀=Bsin(wt);  y₁=Bsin(wt+Dj); y₂=Bsin(wt+2Dj); y₃=Bsin(wt+3Dj);  Механические волны делятся на: а) продольные - колебания среды происходят вдоль направления распространения волн, при этом возникают области сжатия и разрежения среды. - возникают в любой среде (жидкости, в газах, в тв. телах). б) поперечные - колебания среды происходят перпендикулярно направлению их распространения, при этом происходит сдвиг слоев среды. - возникают только в твердых телах.

Амплитуда — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении. Неотрицательная скалярная величина, размерность которой совпадает с размерностью определяемой физической величины. Фаза колебаний — аргумент функции cos(ωt + φ), описывающий гармонический колебательный процесс. Фаза — это величина стоящая под знаком синуса или косинуса в уравнениях гармонических колебаний. 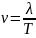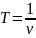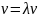Скорость волны определяется скоростью распространения колебаний от одной очки среды к другой: ; Так как   то, Скорость распространения волн тем меньше, чем инертнее среда, т.е. чем больше ее плотность. С другой стороны, она имеет большее значение в более упругой среде, чем в менее упругой. Скорость продольных волн определяется по формуле: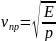  , а поперечной: 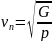, где ρ- плотность среды, E - модуль Юнга, G - модуль сдвига. Так как для большинства твердых тел E>G то скорость продольных волн больше скорости поперечных.