
- •1.Основные кинематические характеристики мат. Точки : радиус-вектор,координаты, перемещение, траектория, путь. Способы описания движения мат. Точки.
- •2.Описание перемещения, скорости и ускорения в векторной и координатной форме.
- •3.Ускорение точки при криволинейном движении. Нормальное и тангенциальное
- •4.Кинематика твердого тела. Число степеней свободы твердого тела. Поступательное движение твердого тела. Вращение вокруг неподвижной оси. Векторы угловой скорости и углового ускорения.
- •5.Связь между линейными и угловыми характеристиками вращательного движения твердого тела.
- •6.Плоское движение твердого тела. Мгновенная ось вращения. Динамика плоского движения.
- •7.Инерциальные систему отсчета. Преобразования Галилея. Инварианты преобразований Галилея. Классический закон сложения скоростей. Механический принцип относительности.
- •8.Взаимодействия и силы. Силы в механике. Первый закон Ньютона.
- •9.Масса тела. Второй и третий законы Ньютона. Интерпретация третьего закона Ньютона при электромагнитном взаимодействии движущихся зарядов.
- •10.Система мат. Точек и ее импульс. Уравнение движения системы мат точек.
- •12.Закон сохранения импульса механической системы.
- •20.Сила трения. Сухое и вязкое трение. Трение покоя. Трение скольжения. Трение качения.
- •21.Закон притяжения Ньютона. Энергия гравитационного взаимодействия.
- •22.Основные законы движения планет и комет.
- •23.Движение искуственных спутников Земли. Первая, вторая, третья космические скорости. Задача двух тел. Приведенная масса.
- •24.Реактивное движение. Уравнение Мещерского.
- •25.Формула Циалковского. Общая характеристика возможностей реактивных двигателей для космических полетов.
- •26.Работа и мощность силы.Потенциальные силы и их работа.
- •27.Потенциальная энергия, закон ее изменения. Нормировка потенциальной энергии. Связь между силой и потенциальной энергией.
- •28.Кинетическая энергия. Закон изменения кинетической энергии для мат точки.
- •29.Кинетическая энергия твердого тела, закон ее изменения.
- •30.Полная механическая энергия мат точки и механической системы. Закон ее изменения. Закон ее сохранения.
- •40.Сложение гармонических колебаний одного направления. Биения.
- •41.Сложение взаимноперпендикулярных колебаний. Фигуры Лиссажу.
- •42.Связанные системы. Парциальные и нормальные колебания. Представление движения системы с помощью нормальных колебаний.
- •43.Продольные и поперечные волны. Амплитуда, фаза, скорость распространения волы.
- •47.Природа звука. Высота звука. Громкость. Звуковое давление. Энергия звуковой волны.
- •48.Скорость звука и ее измерение. Источники звука. Ультразвук. Эффект Доплера.
- •49.Стационарное течение жидкости, поле скоростей. Линии и трубки тока. Уравнение неразрывности струи.
- •51.Полная энергия потока. Уравнение Бернулли.
- •52.Вязкость жидкости. Коэффициент вязкости и его измерение.
27.Потенциальная энергия, закон ее изменения. Нормировка потенциальной энергии. Связь между силой и потенциальной энергией.
Потенциальная энергия — скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет его нахождения в поле действия сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы. Единицей измерения энергии в СИ является Джоуль.
28.Кинетическая энергия. Закон изменения кинетической энергии для мат точки.
кинетическая
энергия - это еще одна, но уже скалярная,
мера движения материальной точки, что
дает ей определенные преимущества
перед векторными мерами движения -
количеством движения и моментом
количества движения. В системе СИ
единицей измерения кинетической энергии
является джоуль, 1 Дж = кг·(м2/с2) =
(кг·м/c2)·м = 1 Н·м. Кинетическая энергия
обозначается буквой Ek. Ek=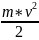
Теорема об изменении кинетической энергии материальной точки.
Для
доказательства теоремы запишем
дифференциальное уравнение движения
точки в виде mdV
/ dt
= F.
Умножая обе части уравнения скалярно
на вектор элементарного действительного
перемещения точки dr
и учитывая, что dr
/ dt
= V,
имеем m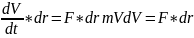
Зная, что F - равнодействующая сил, приложенных к точке, обозначим δA скалярное произведение в правой части и назовем его элементарной работой сил, приложенных к точке:δA=F*dr
Находя
дифференциал от mV2 / 2, имеем d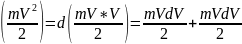 mVdV=d
mVdV=d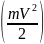
Подставляя
последнее выражение и выражение (2) в
уравнение (1), получаем математическую
запись теоремы в дифференциальной
форме: d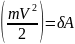
Половину произведения массы точки на квадрат ее скорости под знаком дифференциала в левой части уравнения (3) называют кинетической энергией точки.
Это замечание позволяет по математической записи сформулировать теорему об изменении кинетической энергии материальной точки в дифференциальной форме: дифференциал от кинетической энергии материальной точки равен элементарной работе сил, приложенных к точке.
29.Кинетическая энергия твердого тела, закон ее изменения.
Кинетическая энергия материальной точки - мера ее движения. Характеризует ее способность к совершению работы вследствие движения. Кинетическая энергия материальной точки - скалярная физическая величина, равная половине произведения массы материальной точки на квадрат ее скорости в данной системе отсчета.
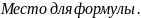
 [Дж]
[Дж]
Теорема о кинетической энергии материальной точки.
В инерциальной
системе отсчета изменение кинетической
энергии материальной точки равно работе
силы, на эту точку действующей.
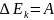
30.Полная механическая энергия мат точки и механической системы. Закон ее изменения. Закон ее сохранения.
. Полная механическая энергия материальной точки - сумма ее кинетической и потеннциальной энергий.
E=Ek+ Ep [Дж]
Полная механическая энергия системы материальных точек - сумма кинетической и потенциальной энергий системы.
E=Ek+ Ep [Дж]
Теорема о полной механической энергии материальной точки.
Изменение полной механической энергии материальной точки в инерциальной системе отсчета равно работе всех непотенциальных сил, действующих на эту точку.E = Aнепот Теорема о полной механической энергии системы материальных точек.
Если на систему материальных точек, движущуюся в инерциальной системе отсчета, действуют как потенциальные, так и непотенциальные силы, то изменение полной энергии системы равно работе всех непотенциальных сил, как внешних, так и внутренних.
E = Aнепот.
Закон сохранения полной механической энергии материальной точки.
Если в инерциальной системе отсчета работа непотенциальных сил, действующих на материальную точку, равна нулю, то полная энергия точки сохраняется.
Aнепот.=0 Ek + Ep = const
