Лекция 15. Решение задачи коши для волнового уравнения

15.1. Решение задачи Коши методом Даламбера

Поставим задачу Коши для однородного волнового уравнения, описывающего свободные колебания однородной струны, т.е. найдем решение уравнения

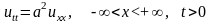, (15.1)

удовлетворяющее начальным условиям

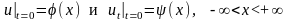. (15.2)

Эту задачу (15.1), (15.2) можно решить методом Даламбера.

Осуществим переход к канонической форме уравнения (15.1) с помощью общих интегралов уравнения характеристик (13.3). В нашем случае это уравнение имеет вид:

Следовательно, С₁ и С₂ определяют уравнения семейств характеристик. Тогда преобразование независимых переменных (13.5) будет иметь вид

.

Вычислим в новых переменных:

и подставим их в уравнение (15.1)

.

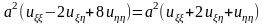После сокращений получим

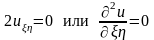. (15.3)

Интегрирование этого уравнения дает

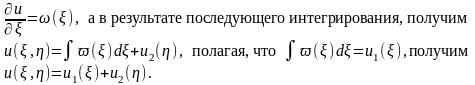
Возвращаясь к переменным х и у, окончательно будем иметь

. (15.4)

Функция является решением уравнения (15.1), если и₁ и и₂ - произвольные дважды дифференцируемые функции. В решении (15.4) необходимо выбрать функции и₁ и и₂ так, чтобы удовлетворить начальным условиям (15.2)

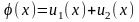(15.5)

и

. (15.6)

Проинтегрировав уравнение (15.6) в пределах от х₀ до х, получим

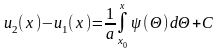. (15.7)

Разрешив совместно уравнения (15.5) и (15.7) относительно и₁(х) и и₂(х), получим

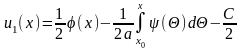(15.8)

(15.9)

Подставив (15.8) и (15.9) в решение (15.4) окончательно получим решение задачи Коши для однородного волнового уравнения

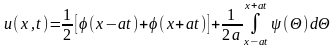. (15.10)

Формула (15.10) называется формулой Даламбера для однородного волнового уравнения, описывающего свободные колебания однородной струны. Эта формула дает классическое решение задачи (15.1) - (15.2) только в предположении, что функция 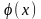имеет производные до второго порядка включительно, а функция 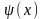- до первого.

Решение задачи Коши неоднородного волнового уравнения, описывающего вынужденные колебания однородной струны

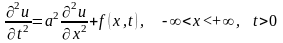, (15.11)

удовлетворяющего начальным условиям

, (15.12)

можно получить по формуле

.(15.13)

Это формула Даламбера, дающая решение задачи Коши для неоднородного волнового уравнения, описывающего вынужденные колебания однородной струны.

Пример 15.1. Найти решение уравнения

,

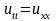удовлетворяющее начальным условиям

.

▲ Для нахождения решения исходной задачи Коши используем формулу Даламбера (15.10)

,

в которой .

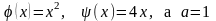Следовательно,

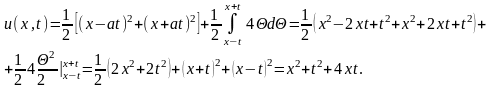Окончательно решение исходной задачи имеет вид

▲

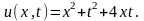Пример 15.2. Найти решение уравнения

,

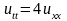удовлетворяющее начальным условиям

.

▲ Для нахождения решения исходной задачи Коши используем формулу Даламбера (15.10)

,

в которой .

Следовательно,

Окончательно решение исходной задачи имеет вид

▲

Пример 15.3. Найти решение уравнения

,

удовлетворяющее начальным условиям

.

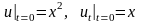▲ Для нахождения решения исходной задачи Коши используем формулу Даламбера (15.13)

в которой .

Следовательно,

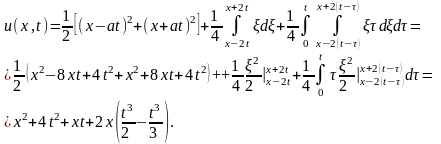Окончательно решение исходной задачи имеет вид

▲

15.2. Решение задачи Коши для волнового уравнения методом Тейлора

Задача Коши для волнового уравнения, описывающего вынужденные колебания какого-либо трехмерного объекта

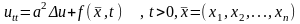(15.14)

с начальными условиями

(15.15)

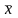где – неизвестная функция; – заданные функции; - вектор с координатами (x,y,z), может быть решена методом Тейлора. Суть метода заключается в том, что решение поставленной задачи ищется в виде ряда

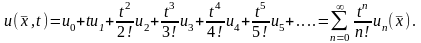(15.16)

Если найти все функции 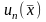, то по формуле (15.16) получим решение исходной задачи Коши. Заметим, что определяются из начальных условий (15.15), остальные коэффициенты можно найти по формуле

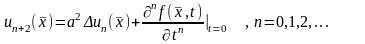(15.17)

Пример 15.4. Найти решение уравнения

▲ Здесь

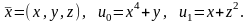
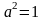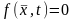Так как и , то по (15.17)

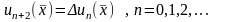
Отсюда, при n = 0, получим

при n = 1, получим

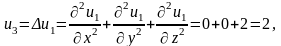
при n = 2, получим

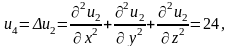
при n = 3, получим

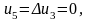
при n = 4, получим

то есть, все остальные

Подставляем найденные в решение (15.16)

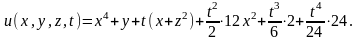
Окончательно,

▲

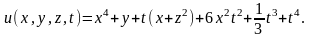Пример 15.5. Найти решение уравнения

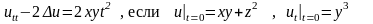
▲ Здесь Так как и , то по (15.17)

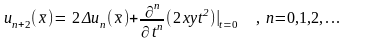
Найдем по этой формуле

И так далее, все остальные

Подставляем полученные в решение (15.16)

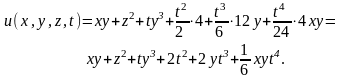
Таким образом, решением исходного уравнения является функция

▲