
- •Часть 2. Дифференциальные уравнения в частных производных первого порядка Лекция 11. Уравнения в частных производных первого порядка
- •11.1. Линейные и квазилинейные уравнения
- •11.2. Уравнения с переменными коэффициентами. Характеристики
- •11.3. Решение задачи Коши
- •12.2. Уравнение колебаний стержня
- •12.3. Уравнение теплопроводности и диффузии
- •12.4. Уравнения гидродинамики и звуковых волн
- •Лекция 13. Классификация уравнений в частных производных 2-го порядка, приведение их к каноническому виду и нахождение общего решения
- •Задания для самостоятельной работы
- •Лекция 14. Начальные и граничные условия
- •14.1. Начальные условия
- •14.2. Краевые задачи
- •Лекция 15. Решение задачи коши для волнового уравнения
- •15.1. Решение задачи Коши методом Даламбера
- •15.2. Решение задачи Коши для волнового уравнения методом Тейлора
- •Задания для самостоятельной работы
- •Лекция 16. Решение граничных задач волнового уравнения
- •16.1. Метод Фурье (метод разделения переменных) для уравнения свободных колебаний струны
- •16.2. Метод Фурье (метод разделения переменных) для уравнения вынужденных колебаний струны
- •Задания для самостоятельной работы
- •Лекция 16 (продолжение). Задача о напряженном состоянии элемента вооружения долота режущего действия
- •Лекция 17. Уравнения теплопроводности (диффузии) и методы их решений
- •17.1. Методы решения задачи Коши
- •Задания для самостоятельной работы
- •17.2. Методы решения граничных задач
- •Лекция 17 (продолжение). Расчет глубины промерзания связанных горных пород
- •Лекция 18. Стационарные уравнения. Уравнение лапласа и методы его решения
- •18.1.Задачи, приводящие к уравнениям эллиптического типа
- •18.2. Решения краевых задач для уравнения Лапласа в круге
- •Задания для самостоятельной работы
- •Лекция 19. Уравнение неразрывности и уравнения эйлера
- •19.1. Гипотеза сплошности
- •19.2. Установившееся и неустановившееся движения.
- •19.3. Уравнения гидродинамики и звуковых волн
- •19.4. Закономерности распространения плоских упругих волн
- •Лекция 20. Закономерности преломления и отражения плоских упругих волн на плоскости контакта твердых тел
- •Часть 4. Преобразование лапласа и его применение при решении дифференциальных уравнений Лекция 21. Преобразование лапласа
- •21.1. Преобразование Лапласа
- •21.2. Основные свойства преобразования Лапласа
- •21.3. Свертка функций
- •21.4. Оригиналы с рациональными изображениями
- •21.5. Нахождение оригинала по заданному изображению (когда оно рационально)
- •21.6. Оригиналы с изображениями, регулярными в бесконечности
- •Лекция 22. Практическое применение преобразования лапласа
- •22.1. Приложения к решению линейных дифференциальных уравнений с постоянными коэффициентами
- •22.2. Использование преобразования Лапласа при решении уравнений в частных производных
- •Лекция 23. Миграционная подмодель радиогеоэкологической модели подземного регионального хранилища радиоактивных отходов и ядерных материалов
- •Вопросы к экзамену по дисциплине: «Дифференциальные уравнения в горном деле»
21.3. Свертка функций
Формула
Дирихле.
Пусть
![]() непрерывна
в треугольнике
непрерывна
в треугольнике
![]() :
:
![]() (рис.
21.1).
(рис.
21.1).
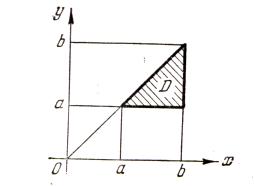
Рис. 21.1
Преобразуя
двойной интеграл
![]() двумя способами в двукратный и сравнивая
результаты, получим искомую формулу
Дирихле:
двумя способами в двукратный и сравнивая
результаты, получим искомую формулу
Дирихле:
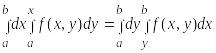 (21.3)
(21.3)
Свертка
функций. Пусть
и
— непрерывные, комплекснозначные
функции на
![]() .
Сверткой
функций
и
называется функция, обозначаемая
.
Сверткой
функций
и
называется функция, обозначаемая
![]() *
*![]() и
определяемая равенством
и
определяемая равенством
(
*
)![]()
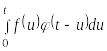 .
.
Это будет непрерывная функция на . Очевидно,
![]() *
*![]()
![]() *
*![]()
при с помощью формулы Дирихле находим:
![]() *
*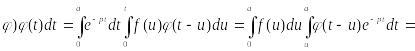
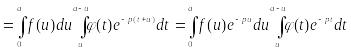 ;
;
следовательно, если записать внутренний интеграл
![]() в
виде
в
виде
![]() -
-![]() ,
получим
формулу
,
получим
формулу
*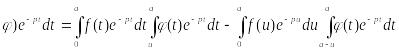 (21.4)
(21.4)
Из
(21.4)
следует, что при
![]() и
и
![]() и действительном
и действительном
![]()
![]() *
* ,
,
откуда видно, что если и оригиналы, то * — тоже оригинал, причем показатель роста * не более наибольшего из показателей роста и .
Свертка оригиналов.
Теорема.
При
свертывании оригиналов изображения
перемножаются, т.е. если
≒
и
≒
,
то
![]() *
*![]() ≒
≒![]() .
.
Доказательство.
Для простоты мы имеем в виду лишь
непрерывные на
![]() оригиналы. Учитывая формулу (19.4),
достаточно показать, что
оригиналы. Учитывая формулу (19.4),
достаточно показать, что
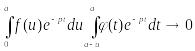 при
.
при
.
Пусть
![]() ≒
≒![]() и
и
![]() ≒
≒![]() ,
тогда,
если Rе
,
тогда,
если Rе![]() больше показателей роста
и
,
то
больше показателей роста
и
,
то
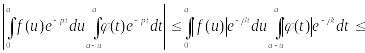
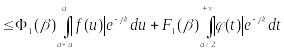 ,
,
что
![]() при
,
что и требовалось доказать.
при
,
что и требовалось доказать.
Пример.
Найти
свертку
![]() и
и
![]() ,
где
,
,
где
,
![]() .
Делая в интеграле подстановку
.
Делая в интеграле подстановку
![]() и
учитывая формулы
и
учитывая формулы
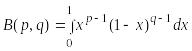 и
и
![]()
![]() ,
,
где
![]() и
и
![]() – гамма-функции, или эйлеровы интегралы
2-го рода, которые определяются для
положительных значений независимых
переменных
и
– гамма-функции, или эйлеровы интегралы
2-го рода, которые определяются для
положительных значений независимых
переменных
и
![]() формулами:
формулами:
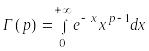 и
и
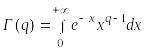 ,
,
*
и, в
частности, при целых неотрицательных
![]() ,
,
![]() и
и
![]()
Следовательно, искомая свертка имеет вид
![]() *
*![]() .
.
Формула
Дюамеля. Пусть
-
непрерывный на
оригинал,
-
непрерывно дифференцируемая на
функция такая, что
![]() есть
оригинал. Из
≒
и
≒
следует:
есть
оригинал. Из
≒
и
≒
следует:
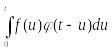 ≒
≒
Из правила дифференцирования интегралов, зависящих от параметра, следует, что левая часть непрерывно дифференцируема на , причем

Отсюда в силу свойства 4 (см. 21.2) [дифференцирование оригинала ] получаем искомую формулу Дюамеля
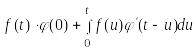 ≒
(21.5)
≒
(21.5)
21.4. Оригиналы с рациональными изображениями
Изображения некоторых элементарных функций.
1.
Изображения
степенных и показательных функций.
При
![]() степенная функция
является оригиналом с нулевым показателем
поста, причем
степенная функция
является оригиналом с нулевым показателем
поста, причем
![]() ,
,
что
при положительных значениях
равно
(после замены
![]() на t)
на t)
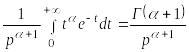 (21.6)
(21.6)
Необходимо
отметить, что в силу теоремы
единственности,
которая гласит: если в области
даны две аналитические функции,
совпадающие на множестве точек, имеющем
хотя бы одну предельную точку, лежащую
в области
,
то эти две функции тождественно равны,
изображение
и правой часть равенства (21.6)
аналитичны в полуплоскости Rе![]() ,
следовательно, совпадая в положительных
точках, они совпадают на всей полуплоскости
Rе
(заметим, что степенные функции
,
следовательно, совпадая в положительных
точках, они совпадают на всей полуплоскости
Rе
(заметим, что степенные функции
![]() комплексного
переменного
многозначны
при нецелых
комплексного
переменного
многозначны
при нецелых
![]() ,
но, рассматривая их на полуплоскости
Rе
,
мы всякий раз имеем в виду те их ветви,
которые происходят от ветвей
,
но, рассматривая их на полуплоскости
Rе
,
мы всякий раз имеем в виду те их ветви,
которые происходят от ветвей
![]() ,
совпадающих
для положительных
с
).
Итак,
,
совпадающих
для положительных
с
).
Итак,
≒![]() (
) (21.7)
(
) (21.7)
Так,
при
![]()
![]()
≒![]() (21.8)
(21.8)
и, в
частности, при
![]()
1≒![]() (21.9)
(21.9)
Из (21.8) по правилу смещения изображений (1.2 свойство 9 - ≒ ) находим при любом целом неотрицательном и любом комплексном
![]() ≒
≒![]() (21.10)
(21.10)
и, в частности, при
![]() ≒
≒![]() (21.11)
(21.11)
2. Изображения тригонометрических и гиперболических функций. В силу (21.10) имеем:
![]() ≒
≒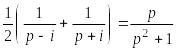 (21.12)
(21.12)
![]() ≒
≒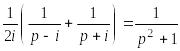 (21.13)
(21.13)
![]() ≒
≒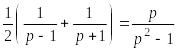 (21.14)
(21.14)
![]() ≒
≒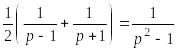 (21.15)
(21.15)
Из (21.12) и (21.13) по правилу подобия (1.2, свойство 3 - ≒ ) находим:
![]() ≒
≒![]() (21.16)
(21.16)
![]() ≒
≒![]() (21.17)
(21.17)
откуда
по правилу смещения изображений (1. 2,
свойство 9 -
![]() ≒
)
≒
)
![]() ≒
≒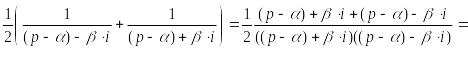
![]() (21.18)
(21.18)
![]() ≒
≒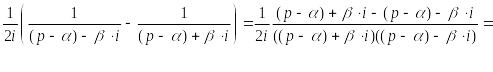
![]() (21.19)
(21.19)
Условие рациональности изображения.
3. Изображения линейной комбинации функций вида .
Изображения линейной комбинации функций вида ( - целое неотрицательное, - комплексное) всегда являются рациональными, т.е. всякая правильная рациональная дробь является изображением некоторого оригинала. Поэтому, с помощью преобразования Лапласа можно устанавить взаимно однозначное соответствие между всеми функциями, являющимися линейными комбинациями выражений tmet, и всеми правильными рациональными дробями.
Необходимо отметить, что класс функций, являющихся линейными комбинациями выражений вида , обладает следующими свойствами:
- операции линейного комбинирования,
- умножения на аргумент,
- умножения на показательную функцию,
- линейного преобразования аргумента,
- дифференцирования и интегрирования,
примененные к функциям этого класса, приводят снова к функциям этого класса.
