Часть 4. Преобразование лапласа и его применение при решении дифференциальных уравнений Лекция 21. Преобразование лапласа

21.1. Преобразование Лапласа

Преобразование Лапласа это такое преобразование, которое ставит в соответствие комплекснозначной функции действительного переменного некоторую функцию комплексного переменного с помощью следующего соотношения

. (21.1)

Интеграл, стоящий в правой части, называют интегралом Лапласа функции . При этом эта функция должна удовлетворять следующим условиям:

1. задана на множестве действительных чисел (на числовой прямой) R, причем для всех функция ;

2. при функция на любом ограниченном промежутке имеет не более чем конечное число точек разрыва первого рода;

3. существуют такие числа и , что для всех функция является ограниченной - , причем точная нижняя граница числа равна числу ( ), которое называется показателем степени роста функции , следовательно, можно констатировать, что функция в данном случае имеет ограниченный рост.

Если функция имеет ограниченный рост, то является аналитической функцией комплексного переменного в полуплоскости Re , где - показатель степени роста функции , который еще называют абсциссой абсолютной сходимости интеграла Лапласа .

Резюмируя сказанное можно утверждать:

- комплекснозначная функция , непрерывная на интервале , за исключением изолированных точек^, и имеющая ограниченный рост, называется оригиналом;

- аналитическая функция комплексного переменного , определенная формулой (21.1) при Re , называется изображением оригинала .

Преобразование Лапласа (21.1) схематично можно записать в виде

≒ .

Употребляется также обозначение вида

,

где - знак преобразования Лапласа.

Замечания.

1. Если функция является оригиналом, то и также будет оригиналом с тем же показателем роста.

2. Если функции , ,…, , являются оригиналами, то их линейная комбинация также будет оригиналом. Если функция является оригиналом, то функции ( - положительное число), , ( – действительное число), ( - комплексное число) тоже будут оригиналами.

3. Можно утверждать, что если комплекснозначная функция является оригиналом, то функция , определяемая выражением

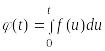
будет непрерывным на интервале оригиналом.

Непрерывность функции следует из абсолютной интегрируемости функции на каждом сегменте , где . Далее, если – показатель степени роста функции , а – положительное число больше , причем ( Re ), то в случае, когда имеем:

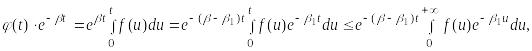
откуда следует, что интеграл 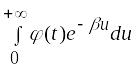сходится, а функция является оригиналом.

4. Если функция комплексного переменного , определенная формулой (21.1) является изображением, то при Re следует, что .

21.2. Основные свойства преобразования Лапласа

1. Однородность. Если ≒ , то ≒ ( - любое комплексное число).

Действительно,

.

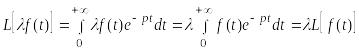Следовательно, ≒ .

2. Аддитивность. Если ≒ и ≒ , то

≒ .

Действительно,

.

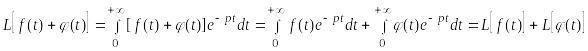Следовательно, ≒ .

3. Подобие. Если ≒ , то ≒ .

Действительно,

.

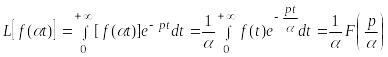Следовательно, ≒ .

4. Дифференцирование оригинала. Если функция непрерывно дифференцируема на интервале является оригиналом и существует конечный предел - , а также, если есть то же оригинал, то из ≒ следует:

≒ .

Действительно, интегрирование по частям дает при

.

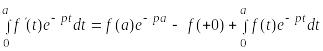Если Re больше показателей роста функции и ее производной , то оба интеграла стремятся к конечным пределам при , следовательно, с учетом того, что интеграл вида 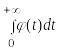не может абсолютно сходиться, если функция при стремится к пределу, отличному от нуля, стремится к конечному пределу, но этот предел не может быть отличен от нуля. Следовательно, в пределе при получим

.

4.1. Обобщение. Если функция раз непрерывно дифференцируема на интервале является оригиналом и все ее производные до -го порядка включительно – , ,…, , то же есть оригиналы, а также существуют конечные пределы - , , ,…, , то из ≒ следует:

≒ .

Для доказательства существования изображения производной -го порядка используется свойство 4 по индукции.

5. Дифференцирование изображения. Если ≒ , то

≒ .

Действительно,

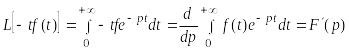
Следовательно, ≒ .

5.1. Обобщение. Если ≒ , то ≒ .

Для доказательства этого утверждения используется метод индукции по свойству 5.

6. Интегрирование оригинала. Если функция являющаяся оригиналом, непрерывна на интервале и имеет изображение , то

≒ .

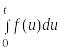Действительно, если функция является оригиналом, которому соответствует изображение , т.е. ≒ , тогда и по свойству 4 следует, что ≒ , следовательно,

или = .

7. Интегрирование изображения. Если функция является оригиналом, а также является оригиналом , то из ≒ следует:

≒ .

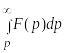
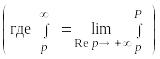Действительно, если ≒ , тогда по свойству 5 ≒ , следовательно, . Интегрируя полученное равенство в пределах от до , найдем:

,

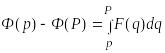следовательно, с учетом того, что Re следует, что , получим:

.

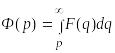8. Запаздывание. Если ≒ , то ≒ ( – любое положительное число).

Действительно,

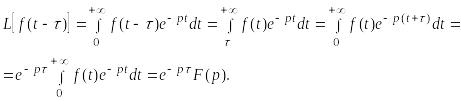
9. Умножение оригинала на показательную функцию (смещение изображения). Если ≒ , то ≒ ( - любое комплексное число).

Действительно,