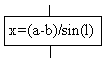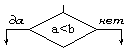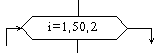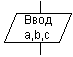7.Дайте определение алгоритма, его особенности.

Под алгоритмом понимается совокупность действий, необходимых для решения задачи. Алгоритм отличается от программы тем, что в нем содержится только описание действий, производимых над данными, но полностью отсутствуют какие-либо описания данных. Алгоритмы содержат определение пошагового процесса обработки данных с описанием преобразований данных и функций управления.

Основные свойства любого алгоритма:

· детерминированность – однозначность получаемых результатов при одних и тех же исходных данных;

· результативность – обязательное получение искомого результата либо сигнала ошибки;

· массовость – возможность получения искомого результата при различных исходных данных;

· дискретность – возможность разбиения на элементарные действия. 1. Однозначность — предлагаемые действия должны быть "понятны" компьютеру, а порядок исполнения этих действий должен быть единственно возможным, любая неопределенность или двусмысленность недопустимы.

Каждая научная дисциплина имеет свои методы получения результатов. Основное различие задач заключается в том, что для одних существуют прямые методы решения, а другие не могут быть решены без дополнительной информации, получаемой в ходе решения задачи.

Если задача может быть решена прямым способом, говорят, что она имеет детерминированный метод решения, в котором отсутствуют неопределенность, произвольность в выборе решений, определяющих последовательность действий. Для синтеза детерминированных алгоритмов недопустимо применение методов проб и ошибок. К таким задачам относятся, в основном, математические уравнения.

Если решение задачи выбирается из заранее определенного множества вариантов, говорят о недетермиинированном методе решения. В реализации недетерминированного алгоритма используются методы проб и ошибок, повторов, случайного выбора. К числу подобных задач относятся задачи оптимизации, транспортные задачи, задачи сортировки и поиска.

Третий тип алгоритмов предназначен не для поиска ответа на поставленную задачу, а для моделирования физических систем с помощью ЭВМ.

Выполнение алгоритмов определяется следующими правилами:

· последовательность действий;

· альтернативность действий;

· использование повторений действий;

· использование вспомогательных алгоримов.

Главная особенность любого алгоритма – формальное исполнение, позволяющее выполнять заданные действия (команды) различным техническим устройствам (исполнителям). Множество команд, которые в состоянии выполнить данный исполнитель, называется системой команд исполнителя. Алгоритм может быть понят и выполнен только в том случае, если каждая его команда входит в эту систему.

3.Графический (блок-схемный) способ записи алгоритмов. Его преимущества и недостатки. Перечислите основные обозначения и приведите пример.

Графический способ представления алгоритмов является более компактным и наглядным по сравнению со словесным.

При графическом представлении алгоритм изображается в виде последовательности  связанных между собой функциональных блоков, каждый из которых соответствует  выполнению одного или нескольких действий.

Такое графическое представление называется схемой алгоритма или блок-схемой. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий.   

Обозначение и пример заполнения	Пояснение
	Вычислительное действие или  последовательность действий
	Проверка условий
	Начало цикла
	Вычисления по подпрограмме,    стандартной подпрограмме
	Ввод-вывод в общем виде
	Начало, конец алгоритма,  вход и выход в подпрограмму
	Вывод результатов на печать

8.Разрешимые и перечислимые множества.

Множество А N называется разрешимым (рекурсивным), если его харак­теристическая функция

вычислима.

Множество А N называется полуразрешимым, если его полухарактеристическая функция

вычислима.

Множество А N называется перечислимым (рекурсивно перечисли­мым), если А = Ø или существует вычислимая последовательность f (т.е. вычислимая тотальная функция f : N —> N), для которой А = {f(0), f(1),...}. Такое представление множества называется его вычислимым пересчетом.

Определения естественно переносятся на случай А ϵ X, где X — про­извольный тип конструктивных объектов (X = N^k, Σ*,...) . При решении задач предполагается использование тезиса Черча-Тьюринга, согласно ко­торому для доказательства вычислимости функции достаточно предложить неформализованный алгоритм ее вычисления.

9.Словесная форма записи алгоритмов. Его преимущества и недостатки, приведите пример.

Словесный способ записи алгоритмов представляет собой описание последовательных этапов обработки данных. Алгоритм задается в произвольном изложении на естественном языке.

Например. Записать алгоритм нахождения наибольшего общего делителя (НОД) двух натуральных чисел (алгоритм Эвклида).

Алгоритм может быть следующим:

• задать два числа;

• если числа равны, то взять любое из них в качестве ответа и остановиться, в противном случае продолжить выполнение алгоритма;

• определить большее из чисел;

• заменить большее из чисел разностью большего и меньшего из чисел;

• повторить алгоритм с шага 2.

• Описанный алгоритм применим к любым натуральным числам и должен приводить к решению поставленной задачи. Убедитесь в этом самостоятельно, определив с помощью этого алгоритма наибольший общий делитель чисел 125 и 75.

Словесный способ не имеет широкого распространения, так как словесные описания:

• строго не формализуемы;

• страдают громоздкостью, то есть многословностью записей;

• допускают неоднозначность толкования отдельных предписаний.

10.Правила составления алгоритмов. В чем суть принципов поэтапной детализации, ограниченного числа структур, модульного принципа.

1. При составлении алгоритма необходимо пользоваться способом последовательной (поэтапной) детализации.

2. Алгоритм должен строиться по модульному принципу.

3.Схема алгоритма должна доставляться на базе ограниченного числа типовых(стандартных) структур.

1.предполагает получение алгоритма в виде многоэтапного, процесса, в котором на каждом из этапов составляется алгоритм или отдельные его части с различной степенью детализации.

2. предполагает его построение в виде отдельных, относительно независимых частей (модулей). В состав модуля включаются части алгоритма, удовлетворяющие следующим требованиям: функциональной законченности, минимальной связности и представимости в форме схемы с одним входом и одним выходом.

Требование функциональной законченности означает, что в состав модуля должна включаться некоторая законченная в смысловом и функциональном отношении часть общего алгоритма. При обнаружении ошибок полной замене или коррекции может подлежать содержание только «неисправного» модуля, а не всего алгоритма.

Требование минимальной связности означает формирование модулей так, чтобы они использовали минимальное число общих переменных. Учет этого требования позволяет строить наглядные и легко «читаемые» алгоритмы, а также выполнять их проверку в автономном режиме.

Представление модуля схемы, имеющей один вход и один выход, так же как и требование минимальной связности, обеспечивает улучшение наглядности и «читаемости» алгоритма. В таких алгоритмах легко прослеживаются причинно-следственные связи отдельных частей.

3.Правило составления схем алгоритмов на базе ограниченного числа типовых структур, имеющих один вход и один выход, обусловлено стремлением обеспечить обозримость и проверяемость алгоритма. Сложные структуры алгоритмов или их частей могут быть изображены с помощью трех типовых структур

обработки данных, имеющих один вход и один выход. При этом алгоритмы сложной структуры также будут иметь один вход и один выход.

К типовым структурам относятся:

1) неразветвленная (линейная) структура обработки данных.

Она характеризуется независимостью последовательности обработки данных от выполнения каких-либо условий;

2) разветвленные нециклические структуры.

Как и в структуре первого типа, степень детализации алгоритма может быть различной. Поэтому внутри символа «Процесс» могут находитьсясвои (внутренние) разветвления, которые можно на этом этапе детализации не учитывать;

3) разветвленные циклические структуры. Структуры этого типа используются для многократного выполнения одних и тех же вычислений (действий) при изменяющихся данных.

11.Приведите примеры алгоритмов с использованием типовых структур алгоритмов.

Различают три типа базовых структур:

• Следование

• Развилка

• Цикл

Пример линейного алгоритма вычисления площади прямоугольника и ее алгоритм в виде блок-схемы:

CLS

INPUT “Введите две стороны прямоугольника”; a,b

S = a * b

PRINT “Площадь”; S

END

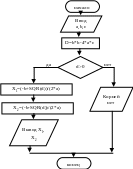
Пример разветвляющегося алгоритма – алгоритм решения квадратного уравнения. Появление условия при решении этой задачи связано с отсутствием корней при отрицательном дискриминанте. Рассмотрим блок-схему этого алгоритма:

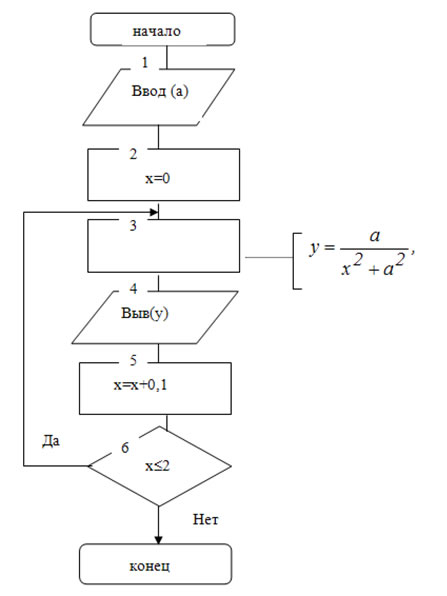
Пример циклического алгоритма. Вычислить если x изменяется от 0 до 2 с шагом 0,1.

Решение: Схема алгоритма имеет вид:

12.Что такое алгоритмизация? Дайте определение и приведите примеры логических и численных алгоритмов.

Алгоритмизация – это процесс построения алгоритма решения задачи, результатом которого является выделение этапов процесса обработки данных, формальная запись содержания этих этапов и определение порядка их выполнения.

Численный алгоритм – алгоритм, соответствующий решению поставленной задачи с помощью арифметических действий.

Логический алгоритм – алгоритм, используемый в случае, если при решении задачи приходится применять некоторые логические действия.

Процесс решения задачи на ЭВМ прежде всего должен быть выражен каким-то алгоритмом. Разработка алгоритмов решения задач – задача программиста, а разработка алгоритмов функционирования цифрового автомата для решения поставленных задач – задача инженера-разработчика.

Пример логического алгоритма.

Приве­дем теперь пример алгоритма, где предписание о спо­собе действия будет относиться уже не к цифровым объ­ектам. Этот алгоритм служит для решения одной логи­ческой задачи — поиска пути в конечном лабиринте.

Представим себе лабиринт в виде конечной системы площадок, от которых расходятся коридоры, причем каждый коридор соединяет две площадки (назовем их смежными площадками), но возможно существование и таких площадок, из которых можно пройти только в один коридор (такие площадки будем называть тупи­ками). Геометрически лабиринт можно представить в виде системы кружков A, В, С, . .., изображающих пло­щадки, соединенные отрезками прямых линий, изобра­жающих коридоры (рис. 12.1).

Алгоритмы, в соответствии с которыми решение по­ставленных задач сводится к арифметическим действиям, называются численными алгоритмами. Рассмотренные выше примеры были примерами численных алгоритмов. Численными алгоритмами также являются любые формулы и схемы, служащие для решения некоторого клас­са задач, если этими формулами полностью выражен как состав действий (умножение, вычитание, деление), так и порядок, в котором они должны выполняться.