Проблемы, касающиеся абстрактных машин

• Проблема остановки

• Проблема самоприменимости

• Busy beaver (англ.)

• Любая проблема, сформулированная в теореме Райса

• Определить, достигнет ли когда-нибудь заданная исходная конфигурация в игре «Жизнь» заданной конечной конфигурации

• ] Проблемы, касающиеся матриц

• Проблема умирающей матрицы: для данного конечного множества квадратных матриц n × n определить, существует ли произведение всех или некоторых из этих матриц (возможно, с повторениями) в каком-либо порядке, дающее нулевую матрицу. Проблема неразрешима даже для n=3 (разрешимость для n=2 является открытым вопросом^[2])

Другие проблемы

• Проблема разрешения (Entscheidungsproblem‎)

• Выводимость формулы в арифметике Пеано

• Проблема соответствий Поста (англ.)

• Вычисление колмогоровской сложности произвольной строки

• Идеальный архиватор, создающий для любого входного файла программу наименьшего возможного размера, печатающую этот файл ^[3]

• Идеальный оптимизирующий по размеру компилятор ^[4]

• Десятая проблема Гильберта

• Определить, можно ли замостить плоскость данным набором плиток Ванга (англ.)

• Определить, можно ли замостить плоскость данным набором полимино

• Проблема унификации (англ.) второго и высшего порядков

• Проблема вывода типов в модели Хиндли — Милнера с rank-N полиморфизмом

Проблемы, алгоритмическая неразрешимость которых не доказана

Для некоторых задач неизвестен алгоритм, решающий их, и по своей природе они похожи на известные алгоритмически неразрешимые задачи. Вопросы об алгоритмической разрешимости таких задач являются открытыми проблемами. Вот некоторые из таких задач:

• Аналог десятой проблемы Гильберта для уравнений степени 3

• Аналог десятой проблемы Гильберта для уравнений в рациональных числах

• Проблема умирающей матрицы для матриц порядка 2

42 Формулировка и доказательство критерия Поста

Теорема:

Набор булевых функций K является полным тогда и только тогда, когда он не содержится полностью ни в одном из классов  , т.е. когда в нем имеется хотя бы одна функция, не сохраняющая ноль, хотя бы одна функция, не сохраняющая один, хотя бы одна несамодвойственная функция, хотя бы одна немонотонная функция и хотя бы одна нелинейная функция.

Доказательство:

Заметим, что необходимость этого утверждения очевидна, так как если бы все функции из набора К входили в один из перечисленных классов, то и все суперпозиции, а значит, и замыкание набора входило бы в этот класс и класс К не мог быть полным. Докажем достаточность этого утверждения. Рассмотрим функцию, не сохраняющую ноль —  .  .   может принимать два значения: а)  , тогда  . б)  , тогда  . Рассмотрим функцию, не сохраняющую один —  .  .   может принимать два значения: а)  , тогда  . б)  , тогда  . Возможны четыре варианта: 1) Мы получили функцию НЕ. Используем несамодвойственную функцию  . По определению найдется такой вектор  , что  .  . Возьмем  , где  , при   и  , при  . Нетрудно заметить, что  . Таким образом мы получили одну из констант. 2) Мы получили НЕ и  .  . 3) Мы получили НЕ и  .  . 4) Мы получили   и  . Рассмотрим немонотонную функцию  . Существуют такие  , что  ,  , зафиксируем все  , тогда  . В итоге имеем три функции: НЕ,  ,  . Используем нелинейную функцию  . Среди нелинейных членов   (ее представления в виде полинома Жегалкина), выберем тот, в котором минимальное количество элементов. Все аргументы, кроме двух, в этом члене, приравняем единице, оставшиеся два назовем   и  , а все элементы, не входящие в данный член, сделаем равными нулю. Тогда эта функция будет представима в виде  , где в квадратных скобках указаны члены, которые могут и не присутствовать (остальные слагаемые будут равны нулю, поскольку в них есть как минимум один аргумент не входящие в выбранный член, т. к. мы выбрали член, в котором минимальное число элементов). Рассмотрим несколько вариантов: Присутствует член  . Возьмем отрицание от   и член   уберется. Присутствуют три члена, без  :  . Составив таблицу истинности для этой функции, нетрудно заметить, что она эквивалентна функции ИЛИ. Присутствуют два члена, без  . Построив две таблицы истинности, для двух различных вариантов, видим, что в обоих случаях функция истинна только в одной точке, следовательно, СДНФ будет состоять только из одного члена, а если это так, то не составляет труда выразить И, через НЕ и  . Присутствует один член. Выразим И, через НЕ и  . В итоге получаем функцию НЕ, а также либо функцию И, либо функцию ИЛИ. Поскольку функцию И можно выразить через ИЛИ и НЕ, а функцию ИЛИ через И и НЕ, то мы получили базис И, ИЛИ, НЕ. Любую булеву функцию, не равную тождественному нулю, можно представить в форме СДНФ, т. е. с помощью данного базиса. Если же функция равна тождественному нулю, то ее можно представить в виде  . Значит, полученные функции образуют полную систему, т. к. с их помощью можно выразить любую булеву функцию. Из этого следует, что K — полная система функций, что и требовалось доказать.

43. Нормальный алгоритм Маркова (НАМ)

НАМ работает с весьма специфической структурой данных, которая называется «строка Маркова» (СМ). СМ представляет собой слово , но в отличие от ленты МТ строка обладает свойством сжатия при замене символов алфавита на «пустой» символ  и расширения при вставлении символов. Это свойство СМ позволяет значительно упростить распознающие алгоритмы, но также значительно усложнить их моделирование на процедурных языках.

Определение НАМ. , А – множество слов в алфавите А, есть строка Маркова в алфавите А, а Р – правила подстановок.

1) , где Т – терминальный алфавит для символов, над которыми работает алгоритм, V – вспомогательный алфавит для промежуточных символов, которые возникают в процессе работы НАМ.

2) Правила Р суть правила замены (подстановки) фрагмента СМ «x» на фрагмент «y». Применение интерпретируется следующим образом:

Пусть , где W, W , W , – строки Маркова, в результате применения правила «x» заменяется на «y» так, что , где и у есть СМ.

а) Если , то (строка Маркова расширяется);

б) Для правила строка Маркова сжимается ровно на х букв.

в) Для правила , где СМ сжимается на .

г) Существует «конечное» правило, отмеченное точкой «» – после его применения НАМ останавливается. Обычно (при правильном завершении НАМ) таким образом фиксируется результат в виде СМ из терминальных букв.

г) Логика исполнения каждого правила может быть описана условным выражением вида: если r = x, то х  у, где r – условие применения правила; или в процедурной записи – if r then

П : х  у, где П – последовательность действий по выполнению замены «х» на «у», некоторым гипотетическим процессором (программой).

3) Процесс выполнения НАМ (производится на единственном процессоре).

а) В каждом такте выполняется единственное правило.

б) Процесс выполнения описывается логической структурой (БСА) и для всех НАМ стандартен (см. рис. 4а). Последовательность выполнения правил может быть произвольной, но фиксированной во время исполнения НАМ.

в) Останов НАМ. После исполнения «конечного» правила ( ) произошло благоприятное завершение, можно «считать» результат из СМ.

г) Аварийный останов НАМ (АО). В процессе выполнения НАМ не может применить ни одного правила. Для распознающего алгоритма аварийный останов АО сигнализирует о ложности предиката .

Пример 6. НАМ для распознавания слов

Правила Условия – Действия

–

–

–

ЛСА этого НАМ показана на рис. 4б. Ниже приводятся примеры работы НАМ при распознавании конкретных слов языка .

а) б) в) г)

(aabb) (abab) (aabbb) (aaabb)

(aSb) (Sab) (aSbb) (aaSb)

ab (SS) – АО (abb) (aab)

(S) (Sb) – АО (aS) – АО

( )

На примере хорошо видно, как сжимается строка Маркова (сравни с соответствующей МТ). Простота построения распознающих алгоритмов на структурах данных типа СМ сделало НАМ весьма популярным как для теории, так и для практики программирования.

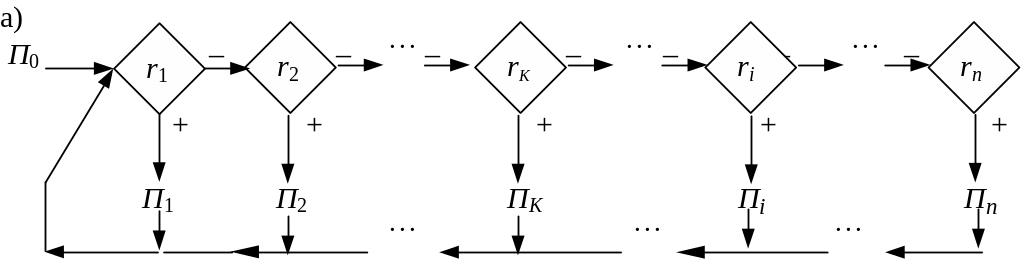
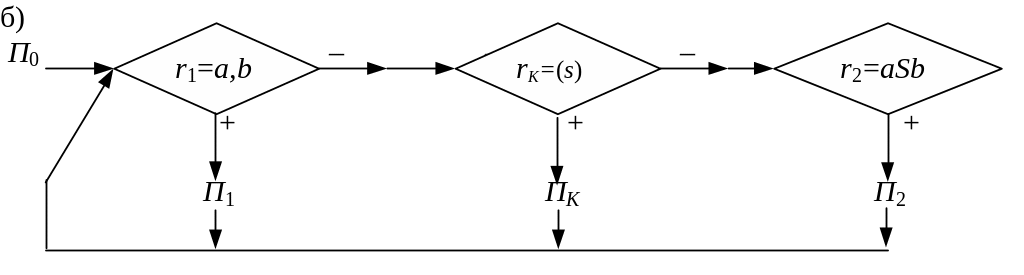
Рис. 4. Логическая структура НАМ.

а) Стандартная логическая структура любого НАМ.

б) Логическая структура НАМ, распознающего слова языка

(без диагностики).

44 пример НАМ