
- •1.Перечислите и поясните основные этапы полного построения алгоритмов.
- •6. Программная реализация алгоритма.
- •4.Сформулируйте основные определения абстрактного алфавита (алфавит, слово алфавита, расширение алфавита, алфавитный оператор).
- •7.Дайте определение алгоритма, его особенности.
- •13.Свойства и виды алгоритмов и соотношение между ними.
- •14.Интерпретации и модели.
- •15.Семантическая и формальная непротиворечивость.
- •1) «Условие – действие», т.Е. Если построенные объекты удовлетворяют некоторым условиям, то для построений нового объекта нужно выполнить такое-то действие;
- •Первая теорема о неполноте
- •22. Интуитивное понятие алгоритма. Требования к алгоритмам.
- •23. Формализация понятия алгоритма и универсальные алгоритмические модели.
- •24.Машина Тьюринга - основные определения. Понятие вычислимости на машине Тьюринга.
- •25.Операции над машинами Тьюринга. Универсальная машина Тьюринга.
- •26.Понятие алгоритмической неразрешимости. Теорема Райса.
- •27.Проблема остановки - формулировка теоремы и ее доказательство.
- •28.Понятие рекурсии. Примитивно-рекурсивные функции. Примеры.
- •29.Неограниченный оператор минимизации. Примеры. Определение частично-рекурсивной функции.
- •30.Разрешимые и перечислимые множества и предикаты.
- •31.Конечные автоматы. Основные определения. Способы задания автоматов.
- •32.Алгоритмические возможности: что могут и что не могут вычислять автоматы. Примеры.
- •33.Эквивалентность автоматов. Алгоритм минимизации автоматов.
- •34.Автоматы и логические схемы. Программная реализация автоматов.
- •35.Интуитивное определение понятия «алгоритм». Свойства алгоритма.
- •37. Приметивно рекурсивные функции
- •Глава 4. Алгоритмы
- •40 Частично рекурсивные функции
- •41 Рекурсивные функции
- •Проблемы, касающиеся абстрактных машин
- •Другие проблемы
- •Проблемы, алгоритмическая неразрешимость которых не доказана
- •42 Формулировка и доказательство критерия Поста
- •Описание
- •Примеры Пример 1
- •Пример 2
- •Ветвление (условный оператор)
- •Повторение (цикл)
- •Устройство машины Тьюринга
- •Проблемы, касающиеся абстрактных машин
- •Другие проблемы
- •Проблемы, алгоритмическая неразрешимость которых не доказана
- •48) Машина Поста
- •Принцип работы
- •Устройство машины Тьюринга
- •Описание машины Тьюринга
- •Полнота по Тьюрингу
- •Варианты машины Тьюринга
- •Машина Тьюринга, работающая на полубесконечной ленте
35.Интуитивное определение понятия «алгоритм». Свойства алгоритма.
Мухаммед ибн Муса ал-Хорезми (IX в) в своем арифметическом трактате изложил основы индийской системы счисления и искусство счета в ней. Латинский перевод трактата, относящийся к XII в начинается словами «Dixit algorizmi» – «Сказал аль-Хорезми». С тех пор термин «алгоритм» стал применяться для обозначения первых алгоритмов цифровых вычислений, затем и для произвольных алгоритмов.
Интуитивное понятие алгоритма – одно из основных понятий математики, не допускающее определения в терминах более простых понятий.
Пусть задано бесконечное множество задач и указано, что понимается под решением каждой из них. Говорят, что существует алгоритм для решения данного бесконечного множества задач, если существует единый способ, позволяющий, для любой задачи этого множества, в конечное число шагов, найти ее решение.
Это не является определением, т.к. выражение «единый», «конечное число шагов» лишены математической точности.
Черты, характерные для интуитивного понятия алгоритма:
Дискретность. Это свойство заключается в следующем: в начальный момент задается исходная система величин, а в каждый следующий момент система величин получается из предыдущей системы величин по определенному закону (программе).
Детерминированность. Система величин, получаемых в любой, отличный от начального, момент времени, однозначно определяется системой величин в предшествующие моменты времени.
Элементарность шагов. Закон получения последующей системы величин из предыдущей должен быть простым и локальным.
Эффективность (результативность). Каждый шаг работы алгоритма должен заканчиваться результатом.
Массовость алгоритма. Начальная система величин может выбираться из некоторого бесконечного счетного множества Х.
Конструктивность. Объекты из Х, над которым работает алгоритм, должны быть конструктивными.
Конструктивный объект – тот, который может быть набран весь целиком и представлен для рассмотрения.
Примерами конструктивных объектов являются булевы функции, формулы алгебры логики, натуральные и рациональные числа, матрицы с натуральными или рациональными элементами, многочлены от неизвестных с рациональными коэффициентами.
Неконструктивными объектами являются, например, любые действительные числа, представления которых в десятичной записи a0 a1…an… ни для какого nиз натуральных чисел не может быть целиком представлено для рассмотрения. Числа и не являются конструктивными объектами.
Понятно, что понятие алгоритма, описываемое свойствами 1-6, является нестрогим: в формулировке этих свойств встречаются слова, не имеющие точного математического определения. Необходимо также отметить, что, вообще говоря, не предполагается, что процесс применения алгоритма к исходным данным обязательно должен закончиться результатом через конечное число шагов. Процесс может закончиться безрезультатно или не закончиться вообще. В этом случае говорят, что алгоритм неприменим к рассматриваемым исходным данным.
Примеры алгоритмов:
-Алгоритмы арифметических действий с числами в двоичной системе счисления
-алгоритм нахождения НОД 2-х целых чисел, 2-х многочленов от переменной х;
-алгоритм извлечения ?n,?n?N ;
-алгоритм дифференцирования многочлена от переменной ;
-алгоритм нахождения определителя квадратной матрицы А над ?;
Вплоть до 30-х годов двадцатого столетия понятие алгоритма оставалось интуитивно понятным, имевшем скорее методологическое, а не математическое значение. Так, к началу ХХ в. много ярких примеров дала алгебра и теория чисел. Среди них упомянем алгоритм Евклида нахождения наибольшего общего делителя двух натуральных чисел или двух целочисленных многочленов, алгоритм Гаусса решения системы линейных уравнений над полем, алгоритм нахождения рациональных корней многочленов одного переменного с рациональными коэффициентами, алгоритм Штурма определения числа действительных корней многочлена с действительными коэффициентами на некотором отрезке действительных чисел, алгоритм разложения многочлена одного переменного над конечным полем на неприводимые множители. Указанные алгоритмические проблемы решены путем указания конкретных разрешающих процедур. Для получения результатов такого типа достаточно интуитивного понятия алгоритма.
Но тогда же были выдвинуты алгоритмические проблемы, для которых не удавалось построить алгоритм, да и само существование таких алгоритмов было под сомнением.
36)
Определение.
Говорят, что функция y получена из функций
j и f1,...,fm
операцией постановки
(суперпозицией)
и обозначают этот факт:
y=Submn(j;f1,...,fm)
или просто y=Sub(j;f1,...,fm),
если
y(x1,x2,...,xn)=j(f1(x1,x2,...,xn),...,fm(x1,x2,...,xn)).
Остановимся на важном применении функций
проецирования, предложенном К.Гёделем
(1934). Заметим, что все функции, определяемые
термами fi,
зависят от n переменных, а функция,
определяемая термом j, имеет столько
переменных, каково количество термов
fi.
Однако иногда требуется найти результат
суперпозиции некоторых функций, но
какое-то из указанных выше условий (все
функции fi
зависят от n переменных, а у функции j
имеется столько переменных, каково
количество функций fi) не выполнены.
Тем не менее, за счет введения фиктивных
аргументов и функций Imn
это можно сделать.
Примеры.
1.
Функция y(x,y,z)=j(f1(x),f2(x,y,z),y,z)
получена суперпозицией из функции
j(x1,x2,x3,x4)
и функций F1(x,y,z)«I13(x,y,z),
F2(x,y,z)«f2(x,y,z),
F3(x,y,z)«I23(x,y,z),
F4(x,y,z)«I33(x,y,z).
2.
Пусть j(x,y,z)«z(x,h(y,q(x)),2). Определение функции
j через функции z,h,q может быть символически
выражено так:
j=Sub33(z;I13,Sub23(h;I23,Sub13(q;I13)),C23).
"Вывод"
можно записывать и следующим образом:
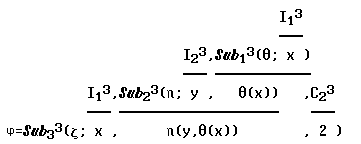 Мы
будем строить класс вычислимых функций,
который будет замкнутым относительно
суперпозиции функций, т.е. если он
содержит некоторые функции, то он
содержит и их суперпозицию. Ответ на
вопрос, почему это так, даёт
следующее
Предложение
(свойства суперпозиции).
Операция
подстановки сохраняет:
(1)
интуитивную вычислимость функций;
(2)
всюду определённость
функций.
Доказательство.
(1)
Если мы каким-либо образом умеем вычислять
значения функций f1,...,fm
и j, то ясно, как надо вычислять значение
функции y. Придадим переменным x1,...,xn
некоторые значения a1,...,an.
Вычислим
все
fi(a1,...,an).
Получим
b1=f1(a1,...,an),...,bm=fm(a1,...,an).
Вычисляя
теперь c=j(b1,...,bm),
получим: y(a1,...,an)=c.
Итак,
если функции f1,...,fm,j
интуитивно вычислимы, то и функция y
интуитивно вычислима.
(2) Если все
функции f1,...,fm
и j - всюду определённые, то функция y
всюду определена. Функция y будет не
всюду определённой, если одна из функций
f1,...,fm
не всюду определена или если можно найти
такие a1,...,an,
что b1=f1(a1,...,an),...,bm=fm(a1,...,an),
но значение j(b1,...,bm)
неопределено.
Предложение доказано.
Мы
будем строить класс вычислимых функций,
который будет замкнутым относительно
суперпозиции функций, т.е. если он
содержит некоторые функции, то он
содержит и их суперпозицию. Ответ на
вопрос, почему это так, даёт
следующее
Предложение
(свойства суперпозиции).
Операция
подстановки сохраняет:
(1)
интуитивную вычислимость функций;
(2)
всюду определённость
функций.
Доказательство.
(1)
Если мы каким-либо образом умеем вычислять
значения функций f1,...,fm
и j, то ясно, как надо вычислять значение
функции y. Придадим переменным x1,...,xn
некоторые значения a1,...,an.
Вычислим
все
fi(a1,...,an).
Получим
b1=f1(a1,...,an),...,bm=fm(a1,...,an).
Вычисляя
теперь c=j(b1,...,bm),
получим: y(a1,...,an)=c.
Итак,
если функции f1,...,fm,j
интуитивно вычислимы, то и функция y
интуитивно вычислима.
(2) Если все
функции f1,...,fm
и j - всюду определённые, то функция y
всюду определена. Функция y будет не
всюду определённой, если одна из функций
f1,...,fm
не всюду определена или если можно найти
такие a1,...,an,
что b1=f1(a1,...,an),...,bm=fm(a1,...,an),
но значение j(b1,...,bm)
неопределено.
Предложение доказано.
Определение.
Будем говорить, что функция
f(x1,...,xn,y)
получена из функций g и h в результате
применения операции
примитивной рекурсии,
если:
(а) для n¹0 имеют место
равенства
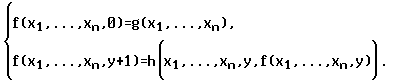 Эта
система равенств называется схемой
примитивной рекурсии с параметрами
x1,...,xn
(первое равенство называется начальным
условием, а второе - рекурсивным
шагом);
(б) для n=0 имеют место
равенства (qÎN)
Эта
система равенств называется схемой
примитивной рекурсии с параметрами
x1,...,xn
(первое равенство называется начальным
условием, а второе - рекурсивным
шагом);
(б) для n=0 имеют место
равенства (qÎN)
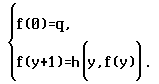 Эта
система равенств называется схемой
примитивной рекурсии без
параметров.
Функцию,
полученную операцией примитивной
рекурсии, обозначим: (а) для n=0:
f(x)=Rec(q,h(x,y)) или f=Rec(q,h); (б) для
n¹0:
f(x1,...,xn,y)=Rec(g(x1,...,xn),h(x1,...,xn,y,z))
или f(x1,...,xn,y)=Recn(g(x1,...,xn),h(x1,...,xn,y,z)),
или f=Rec(g,h), или f=Recn(g,h).
Примеры
(схем примитивной рекурсии).
1.
g(x)«0, 2. g(x)«1, 3. g(x)«x,
h(x,y,z)«z+x, h(x,y,z)«z×x,
h(x,y,z)«xz,
Эта
система равенств называется схемой
примитивной рекурсии без
параметров.
Функцию,
полученную операцией примитивной
рекурсии, обозначим: (а) для n=0:
f(x)=Rec(q,h(x,y)) или f=Rec(q,h); (б) для
n¹0:
f(x1,...,xn,y)=Rec(g(x1,...,xn),h(x1,...,xn,y,z))
или f(x1,...,xn,y)=Recn(g(x1,...,xn),h(x1,...,xn,y,z)),
или f=Rec(g,h), или f=Recn(g,h).
Примеры
(схем примитивной рекурсии).
1.
g(x)«0, 2. g(x)«1, 3. g(x)«x,
h(x,y,z)«z+x, h(x,y,z)«z×x,
h(x,y,z)«xz,
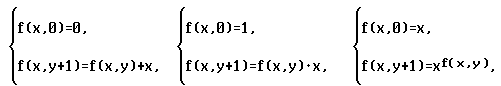 Оказывается
(это можно доказать методом математической
индукции), что приведённые схемы
описывают соответственно
функции:
x
x
f(x,y)=x×y;
f(x,y)=xy;
f(x,2)=x ,...
Мы будем строить
класс вычислимых функций, который будет
замкнутым относительно операции
примитивной рекурсии, т.е. если он
содержит некоторые функции из строящегося
класса, то он содержит и результат
применения к ним операции примитивной
рекурсии. Ответ на вопрос, почему это
так, даёт следующее
Предложение
(свойства операции примитивной рекурсии).
Операция
примитивной рекурсии сохраняет:
(1)
всюду определённость функций;
(2)
интуитивную вычислимость
функций.
Доказательство.
(1) Действительно, пусть f=Rec(g,h), и
функции g(x1,...,xn)
и h(x1,...,xn,y,z)
всюду определены. Докажем, что функция
f определена на любом наборе (x1,...,xn,y).
Проведём доказательство индукцией по
y. (а) y=0, тогда f(x1,...,xn,0)=g(x1,...,xn),
а т.к. функция g всюду определена, то
функция f на наборе (x1,...,xn,0)
также определена. (б) Пусть на наборе
(x1,...,xn,y)
функция f определена. Тогда по определению
операции примитивной рекурсии
f(x1,...,xn,y+1)=h(x1,...,xn,y,f(x1,...,xn,y)).
В
силу всюду определённости функции h,
получаем, что функция f определена на
наборе (x1,...,xn,y+1),
а т.к. f:Nn+1®N
- арифметическая функция, то метод
математической индукции позволяет
сделать вывод, что функция f всюду
определена.
(2) Аналогично тому,
как это делалось для операции подстановки,
можно показать, что если функции g и
h интуитивно вычислимы и f=Rec(g,h), то
существует и алгоритм af, вычисляющий
функцию f. Этот алгоритм состоит в
следующем. Пусть задан некоторый набор
(x1,...,xn,y).
Применяем алгоритм ag,
вычисляющий функцию g, к набору (x1,...,xn).
В случае остановки через конечное число
шагов получаем значение функции g на
наборе (x1,...,xn),
равное, по определению, f(x1,...,xn,0).
После этого используем алгоритм ah,
вычисляющий функцию h, применяя его
последовательно к
наборам
(x1,...,xn,0,f(x1,...,xn,0)),
(x1,...,xn,1,f(x1,...,xn,1)),...,
(x1,...,xn,y-1,f(x1,...,xn,y-1)).
Если
каждый раз работа алгоритма ah заканчивается
остановкой, в результате мы получим
соответственно
значения:
h(x1,...,xn,1,f(x1,...,xn,1))=f(x1,...,xn,2),...,
h(x1,...,xn,y-1,f(x1,...,xn,y-1))=f(x1,...,xn,y).
Если
же не произошло остановки алгоритма ag
при работе на наборе (x1,...,xn)
или не закончилась результативно
работа алгоритма ah
на
одном из этапов (при вычислении
h(x1,...,xn,yl,f(x1,...,xn,yl-1))
для какого-то ylÎ{0,1,...,y-1}),
то перехода к следующему этапу никогда
не произойдет, и искомый алгоритм af
считаем неприменимым к набору
(x1,...,xn,y).
Предложение
доказано.
Таким образом, наш метод
описания класса функций состоит в отборе
функций, получаемых с помощью рекурсивных
определений.
МетаОпределение
(содержательное).
(1)
Рекурсивным
определением
(лат.recurso, recurro) - "бежать назад,
возвращаться") называется определение,
которое основывается на "возвращении"
от неизвестного к известному.
(2)
Рекурсивное
определение функции
- это определение, в котором значения
функции для данных аргументов
непосредственно определяются значениями
той же функции для "более простых"
аргументов или значениями "более
простых" функций. Термин "более
простой" следует уточнять выбором
формализаций (простейшими, как правило,
являются все константы).
Оказывается
(это можно доказать методом математической
индукции), что приведённые схемы
описывают соответственно
функции:
x
x
f(x,y)=x×y;
f(x,y)=xy;
f(x,2)=x ,...
Мы будем строить
класс вычислимых функций, который будет
замкнутым относительно операции
примитивной рекурсии, т.е. если он
содержит некоторые функции из строящегося
класса, то он содержит и результат
применения к ним операции примитивной
рекурсии. Ответ на вопрос, почему это
так, даёт следующее
Предложение
(свойства операции примитивной рекурсии).
Операция
примитивной рекурсии сохраняет:
(1)
всюду определённость функций;
(2)
интуитивную вычислимость
функций.
Доказательство.
(1) Действительно, пусть f=Rec(g,h), и
функции g(x1,...,xn)
и h(x1,...,xn,y,z)
всюду определены. Докажем, что функция
f определена на любом наборе (x1,...,xn,y).
Проведём доказательство индукцией по
y. (а) y=0, тогда f(x1,...,xn,0)=g(x1,...,xn),
а т.к. функция g всюду определена, то
функция f на наборе (x1,...,xn,0)
также определена. (б) Пусть на наборе
(x1,...,xn,y)
функция f определена. Тогда по определению
операции примитивной рекурсии
f(x1,...,xn,y+1)=h(x1,...,xn,y,f(x1,...,xn,y)).
В
силу всюду определённости функции h,
получаем, что функция f определена на
наборе (x1,...,xn,y+1),
а т.к. f:Nn+1®N
- арифметическая функция, то метод
математической индукции позволяет
сделать вывод, что функция f всюду
определена.
(2) Аналогично тому,
как это делалось для операции подстановки,
можно показать, что если функции g и
h интуитивно вычислимы и f=Rec(g,h), то
существует и алгоритм af, вычисляющий
функцию f. Этот алгоритм состоит в
следующем. Пусть задан некоторый набор
(x1,...,xn,y).
Применяем алгоритм ag,
вычисляющий функцию g, к набору (x1,...,xn).
В случае остановки через конечное число
шагов получаем значение функции g на
наборе (x1,...,xn),
равное, по определению, f(x1,...,xn,0).
После этого используем алгоритм ah,
вычисляющий функцию h, применяя его
последовательно к
наборам
(x1,...,xn,0,f(x1,...,xn,0)),
(x1,...,xn,1,f(x1,...,xn,1)),...,
(x1,...,xn,y-1,f(x1,...,xn,y-1)).
Если
каждый раз работа алгоритма ah заканчивается
остановкой, в результате мы получим
соответственно
значения:
h(x1,...,xn,1,f(x1,...,xn,1))=f(x1,...,xn,2),...,
h(x1,...,xn,y-1,f(x1,...,xn,y-1))=f(x1,...,xn,y).
Если
же не произошло остановки алгоритма ag
при работе на наборе (x1,...,xn)
или не закончилась результативно
работа алгоритма ah
на
одном из этапов (при вычислении
h(x1,...,xn,yl,f(x1,...,xn,yl-1))
для какого-то ylÎ{0,1,...,y-1}),
то перехода к следующему этапу никогда
не произойдет, и искомый алгоритм af
считаем неприменимым к набору
(x1,...,xn,y).
Предложение
доказано.
Таким образом, наш метод
описания класса функций состоит в отборе
функций, получаемых с помощью рекурсивных
определений.
МетаОпределение
(содержательное).
(1)
Рекурсивным
определением
(лат.recurso, recurro) - "бежать назад,
возвращаться") называется определение,
которое основывается на "возвращении"
от неизвестного к известному.
(2)
Рекурсивное
определение функции
- это определение, в котором значения
функции для данных аргументов
непосредственно определяются значениями
той же функции для "более простых"
аргументов или значениями "более
простых" функций. Термин "более
простой" следует уточнять выбором
формализаций (простейшими, как правило,
являются все константы).
