
- •1.Перечислите и поясните основные этапы полного построения алгоритмов.
- •6. Программная реализация алгоритма.
- •4.Сформулируйте основные определения абстрактного алфавита (алфавит, слово алфавита, расширение алфавита, алфавитный оператор).
- •7.Дайте определение алгоритма, его особенности.
- •13.Свойства и виды алгоритмов и соотношение между ними.
- •14.Интерпретации и модели.
- •15.Семантическая и формальная непротиворечивость.
- •1) «Условие – действие», т.Е. Если построенные объекты удовлетворяют некоторым условиям, то для построений нового объекта нужно выполнить такое-то действие;
- •Первая теорема о неполноте
- •22. Интуитивное понятие алгоритма. Требования к алгоритмам.
- •23. Формализация понятия алгоритма и универсальные алгоритмические модели.
- •24.Машина Тьюринга - основные определения. Понятие вычислимости на машине Тьюринга.
- •25.Операции над машинами Тьюринга. Универсальная машина Тьюринга.
- •26.Понятие алгоритмической неразрешимости. Теорема Райса.
- •27.Проблема остановки - формулировка теоремы и ее доказательство.
- •28.Понятие рекурсии. Примитивно-рекурсивные функции. Примеры.
- •29.Неограниченный оператор минимизации. Примеры. Определение частично-рекурсивной функции.
- •30.Разрешимые и перечислимые множества и предикаты.
- •31.Конечные автоматы. Основные определения. Способы задания автоматов.
- •32.Алгоритмические возможности: что могут и что не могут вычислять автоматы. Примеры.
- •33.Эквивалентность автоматов. Алгоритм минимизации автоматов.
- •34.Автоматы и логические схемы. Программная реализация автоматов.
- •35.Интуитивное определение понятия «алгоритм». Свойства алгоритма.
- •37. Приметивно рекурсивные функции
- •Глава 4. Алгоритмы
- •40 Частично рекурсивные функции
- •41 Рекурсивные функции
- •Проблемы, касающиеся абстрактных машин
- •Другие проблемы
- •Проблемы, алгоритмическая неразрешимость которых не доказана
- •42 Формулировка и доказательство критерия Поста
- •Описание
- •Примеры Пример 1
- •Пример 2
- •Ветвление (условный оператор)
- •Повторение (цикл)
- •Устройство машины Тьюринга
- •Проблемы, касающиеся абстрактных машин
- •Другие проблемы
- •Проблемы, алгоритмическая неразрешимость которых не доказана
- •48) Машина Поста
- •Принцип работы
- •Устройство машины Тьюринга
- •Описание машины Тьюринга
- •Полнота по Тьюрингу
- •Варианты машины Тьюринга
- •Машина Тьюринга, работающая на полубесконечной ленте
31.Конечные автоматы. Основные определения. Способы задания автоматов.
Конечный автомат — абстрактный автомат без выходного потока, число возможных состояний которого конечно. Результат работы автомата определяется по его конечному состоянию.
Существуют
различные варианты задания конечного
автомата. Например, конечный автомат
может быть задан с помощью пяти
параметров: ![]() ,
где:
,
где:
Q — конечное множество состояний автомата;
q0 — начальное состояние автомата (
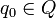 );
);F — множество заключительных (или допускающих) состояний, таких что
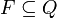 ;
;Σ — допустимый входной алфавит (конечное множество допустимых входных символов), из которого формируются строки, считываемые автоматом;
δ — заданное отображение множества
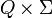 во
множество
во
множество 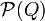 подмножеств
Q:
подмножеств
Q:
![]() (иногда
δ называют функцией
переходов автомата).
(иногда
δ называют функцией
переходов автомата).
Автомат начинает работу в состоянии q0, считывая по одному символу входной строки. Считанный символ переводит автомат в новое состояние из Q в соответствии с функцией переходов. Если по завершении считывания входного слова (цепочки символов) автомат оказывается в одном из допускающих состояний, то слово «принимается» автоматом. В этом случае говорят, что оно принадлежит языку данного автомата. В противном случае слово «отвергается».
Конечные автоматы широко используются на практике, например в синтаксических, лексических анализаторах, и тестировании программного обеспечения на основе моделей.
Способы описания:
Диаграмма состояний (или иногда граф переходов) — графическое представление множества состояний и функции переходов. Представляет собой нагруженный однонаправленный граф, вершины которого — состояния КА, ребра — переходы из одного состояния в другое, а нагрузка — символы, при которых осуществляется данный переход. Если переход из состояния q1 в q2 может быть осуществлен при появлении одного изнескольких символов, то над дугой диаграммы (ветвью графа) должны быть надписаны все они.
Таблица переходов — табличное представление функции δ. Обычно в такой таблице каждой строке соответствует одно состояние, а столбцу — один допустимый входной символ. В ячейке на пересечении строки и столбца записывается действие, которое должен выполнить автомат, если в ситуации, когда он находился в данном состоянии на входе он получил данный символ.
Детерминированность: Конечные автоматы подразделяются на детерминированные и недетерминированные.
Детерминированным конечным автоматом (ДКА) называется такой автомат, в котором для каждой последовательности входных символов существует лишь одно состояние, в которое автомат может перейти из текущего.
Недетерминированный конечный автомат (НКА) является обобщением детерминированного.
Существует теорема, гласящая, что «Любой недетерминированный конечный автомат может быть преобразован в детерминированный так, чтобы их языки совпадали» (такие автоматы называются эквивалентными). Однако, поскольку количество состояний в эквивалентном ДКА в худшем случае растёт экспоненциально с ростом количества состояний исходного НКА, на практике подобная детерминизация не всегда возможна. Кроме того, конечные автоматы с выходом в общем случае не поддаются детерминизации. В силу последних двух замечаний, несмотря на бо́льшую сложность недетерминированных конечных автоматов, для задач, связанных с обработкой текста, преимущественно применяются именно НКА.
Детерминированным конечным автоматом называется произвольная пятерка <Q,Z,b,s,F> , такая что Q и Z — конечные множества, Пусть M = <Q,Z,b,s,F> — детерминированный конечный автомат. Множество Z называется алфавитом автомата M ( автоматы являются устройствами для распознавания языков; если автомат служит для распознавания языка некоторого алфавита Z, то то же самое Z будет алфавитом этого автомата). Множество Q называется множеством состояний автомата M, а элементы этого множества — состояниями. Поскольку в определение автомата входит s — элемент Q, то множество состояний не может быть пустым. Сам элемент s из опре- деления M называется начальным состоянием автомата M. Множество F называется множеством конечных состояний автомата M, а его элементы — конечными состояниями. Наконец, b называется функцией переходов; если для q1, q2 принадл Q и a принадл Z q2 = b(q1; a), то мы говорим, что автомат M переходит из состояния q1 в состояние q2 под действием символа a.
Конечные автоматы принято изображать в виде диаграмм, на кото рых кружочками отмечены состояния автоматов, а стрелками с надпи санными над ними символами — переходы между состояниями. Начальное состояние автомата отмечается на диаграмме в виде маленького треугольника напротив соответствующего кружочка. Конечные состояния обводятся двойными кружками.
