
- •Основные допущения и гипотезы сопротивления материалов
- •Расчетная схема. Классификация расчетных схем по геометрическому признаку
- •Внешние силы. Силы массовые и поверхностные. Сосредоточенные силы
- •Принципы сопротивления материалов: неизменяемости начальных размеров, независимости действия сил, Сен-Венана.
- •Механические характеристики материалов
- •Внутренние силы. Метод сечений. Внутренние силовые факторы
- •Метод сечений.
- •Внутренние силовые факторы.
- •Напряжения и деформации Напряжение.
- •Растяжение и сжатие. Удлинения и деформации при растяжении и сжатии
- •Коэффициенты запаса прочности и допускаемые напряжения
- •Закон Гука при растяжении и сжатии
- •Определение перемещений при растяжении (сжатии)
- •Закон парности касательных напряжений (из напряжений по косым площадкам)
- •Расчёты на прочность (проектировочный, проверочный, определение несущей способности)
- •Напряженное состояние при растяжении и сжатии (напряжения по косым площадкам)
- •Статически неопределимые системы, работающие на растяжение и сжатие
- •Свойства статически неопределимых систем.
- •Расчет статически неопределимых систем, работающих на растяжение и сжатие за пределами упругости
- •Особенности расчета за пределами упругости.
- •Предельное состояние системы, работающей на растяжение.
- •Чистый сдвиг. Закон Гука при чистом сдвиге. Связь между модулем упругости и модулем сдвига
- •Кручение стержней круглого поперечного сечения
- •Угловое перемещение при кручении и условие жёсткости при кручении (определение касательных напряжений при кручении)
- •Расчет полых валов
- •Кручение стержней прямоугольного поперечного сечения
- •Моменты сопротивления плоских сечений (прямоугольное, круглое, составные сечения)
- •Кручение тонкостенных стержней открытого профиля
- •Кручение тонкостенных стержней замкнутого профиля
- •Статически неопределимые задачи кручения
- •Геометрические характеристики поперечных сечений. Статические моменты и моменты инерции и их свойства.
- •Статические моменты.
- •Преобразование моментов инерции при параллельном переносе осей
- •Моменты инерции простейших фигур (прямоугольник, треугольник, круг)
- •Преобразование моментов инерции при повороте осей
- •Главные оси и главные моменты инерции
- •Изгиб. Внутренние силовые факторы при изгибе
- •Дифференциальные зависимости при изгибе
- •Напряжения при чистом изгибе
- •Расчеты на прочность при изгибе. Рациональные типы сечений при изгибе
- •Напряжения при поперечном изгибе. Формула Журавского
- •Косой изгиб
- •Напряжения при косом изгибе.
- •Внецентренное растяжение и сжатие
- •Перемещения при изгибе. Дифференциальное уравнение изогнутой оси
- •Интегрирование уравнения изогнутой оси по методу начальных параметров
- •Теорема о работе силы, приложенной к линейно упругой системе
- •Теорема Кастилиано
- •Метод Мора. Интеграл Мора
- •Вычисление интеграла Мора по методу Верещагина
- •Кинематический анализ плоских стержневых систем. Статически неопределимые рамы и балки
- •Метод сил. Уравнения метода сил.
- •Использование симметрии и косой симметрии при расчете рам и балок
- •Правило:
- •Расчет статически неопределимых балок
- •Проверка правильности раскрытия статической неопределимости.
Определение перемещений при растяжении (сжатии)
Если нормальная сила и поперечное сечение меняются по длине ступенчато, то стержень надо разбить на участки, так чтобы в пределах каждого участка и были постоянны, определить удлинение каждого из участков и тогда полное удлинение стержня будет равняться алгебраической сумме, (знак определяется знаком ) удлинений участков.
Е сли же напряженное состояние в стержне неоднородно, то выделив малый элемент длиной определим его удлинение
, Здесь и рассматривается как функции z. Полное удлинение стержня будет равно:
16)
Закон парности касательных напряжений (из напряжений по косым площадкам)
Выясним, каковы касательные напряжения
по площадке перпендикулярной данной,
т.е. задаваемой углом
![]()
![]() т.е.
т.е.
![]()
З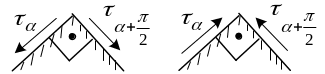 нак
“минус” указывает на то, что касательные
напряжения на взаимно перпендикулярных
площадках направлены либо к ребру между
площадками либо от ребра. Таким образом
имеет место закон парности касательных
напряжений.
нак
“минус” указывает на то, что касательные
напряжения на взаимно перпендикулярных
площадках направлены либо к ребру между
площадками либо от ребра. Таким образом
имеет место закон парности касательных
напряжений.
Касательные напряжения по взаимно перпендикулярным площадкам равны по величине и направлены как было указано выше.
17)
Расчёты на прочность (проектировочный, проверочный, определение несущей способности)
18)
Напряженное состояние при растяжении и сжатии (напряжения по косым площадкам)
Во вводной лекции мы уже упоминали о напряженном состоянии в точке и в частности, говорили, что знать напряженное состояние в точке – это уметь вычислить напряжения по любой площадке, проходящей через данную точку. Теперь уже мы рассмотрим этот вопрос в случае, когда исследуемая точка принадлежит растянутому или сжатому стержню.
П усть
стержень растянут силой F
и в поперечных сечениях стержня, как мы
знаем, возникают нормальные напряжения
равные
усть
стержень растянут силой F
и в поперечных сечениях стержня, как мы
знаем, возникают нормальные напряжения
равные
![]() ,
где А - площадь поперечного сечения.
,
где А - площадь поперечного сечения.
Проведем через
исследуемую точку А произвольное
сечение, положение которого задается
углом
![]() между осью стержня и внешней нормалью
к сечению. Кроме того, проведем еще
поперечное сечение. Выделим с помощью
указанных сечений элемент и рассмотрим
равновесие данного элемента.
между осью стержня и внешней нормалью
к сечению. Кроме того, проведем еще
поперечное сечение. Выделим с помощью
указанных сечений элемент и рассмотрим
равновесие данного элемента.
По наклонной
площадке действует полное напряжение
![]() .
проектируя силы, действующие на элемент
на ось стержня, получаем
.
проектируя силы, действующие на элемент
на ось стержня, получаем
![]()
![]()
Разлагая
на нормальное
![]() и касательное напряжение, получаем
и касательное напряжение, получаем
![]()
![]()
Переходя к функциям
угла
![]() имеем
имеем
![]()
Уравнения (5) дают
возможность вычислить напряжения по
любым площадкам, проходящим через данную
точку, т.е. определяют напряженное
состояние при растяжении и сжатии.
Очевидно, что касательные напряжения
обращаются в нуль по двум площадкам
![]() (поперечное сечение) и
(поперечное сечение) и
![]() (продольное сечение). Площадки, по которым
касательные напряжения равны нулю,
называются главными площадками, а
нормальные напряжения, действующие по
ним, главными напряжениями.
(продольное сечение). Площадки, по которым
касательные напряжения равны нулю,
называются главными площадками, а
нормальные напряжения, действующие по
ним, главными напряжениями.
Очевидно, что одно
из главных напряжений, действующее в
поперечном сечении -
![]() является максимальным по модулю, что
обосновывает использование формулы
(1), как основной расчетной формулы при
растяжении, сжатии, а другое главное
напряжение, действующее в продольных
площадках рано нулю. Таким образом,
продольные площадки свободны от
напряжений.
является максимальным по модулю, что
обосновывает использование формулы
(1), как основной расчетной формулы при
растяжении, сжатии, а другое главное
напряжение, действующее в продольных
площадках рано нулю. Таким образом,
продольные площадки свободны от
напряжений.
Из второго уравнения
(5) видно, что максимальные касательные
напряжения возникают по площадкам,
наклоненным к оси на угол
![]() ,
и равняются по величине
,
и равняются по величине
![]()
Максимальные касательные напряжения являются причиной разру-
шения образцов из хрупких материалов, испытываемых на сжатие.
19)_А
