Перемещения при изгибе. Дифференциальное уравнение изогнутой оси

42)

Интегрирование уравнения изогнутой оси по методу начальных параметров

43)

Теорема о работе силы, приложенной к линейно упругой системе

Работа статической силы, приложенной к упругой системе, равняется половине произведения окончательного значения силы на окончательное значение перемещения.

Пусть - сила, изменяющаяся на сегменте а

- перемещение, изменяющееся в пределах . Система линейно упруга и сила связана с перемещением законом Гука , где - перемещение, вызванное силой Тогда

Э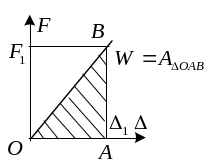 та теорема, носящая имя Клапейрона, имеет простую геометрическую интерпретацию.

Легко понять, что множитель у работы, равный появляется по той причине, что сила не постоянна, а меняется по линейному закону.

44)

Потенциальная энергия деформации при растяжении и сжатии

45)

Потенциальная энергия деформации при кручении

46)

Потенциальная энергия деформации при изгибе

47)

Теорема о взаимности работ и перемещений

Работа первой силы на перемещении ее точки приложения, вызванном второй силой равняется работе второй силы на перемещении ее точки приложения, вызванном первой силой.

Будем считать, что система консервативна и работа в ней не зависит от промежуточных состояний, а зависит лишь от начального и конечного состояния системы.

(Линейно-упругие системы всегда консервативны, если загружены консервативными силами, т.е. силами, имеющими потенциал).

В качестве модели системы выберем консольную балку. Перемещения будем обозначать - перемещение по направлению силы , вызванное силой .

Нагрузим систему вначале силой , а затем приложим силу . Работа сил, приложенных к системе запишется:

(Почему два первых члена имеют множитель , а последний нет?)

Затем первой приложим силу а второй - .

Т.к. система консервативна, а также потому, что начальные и конечные состояния в обоих случаях совпадают, то работы необходимо равны, откуда следует

Если положить , то получим частный случай теоремы Бетти – теорему о взаимности перемещений.

Перемещения, вызванные единичными силами, мы будем обозначать (смысл индексов прежний). Тогда

48)

Теорема Кастилиано

Выражение (3) показывает, что потенциальная энергия деформации является однородной квадратичной функцией и , а те в свою очередь линейно зависят от сил, действующих на систему таким образом является квадратичной функцией сил.

Теорема. Частная производная от потенциальной энергии по силе равняется перемещению точки приложения этой силы по направлению последней.

Доказательство:

Пусть - потенциальная энергия, соответствующая силам системы Рассмотрим два случая.

1) Вначале приложены все силы а затем одна из них получает малое приращение тогда полная потенциальная энергия равна:

2) Вначале приложена сила а затем прикладываются силы В этом случае потенциальная энергия равна:

Т.к. начальное и конечное состояние в обоих случаях одинаково, а система консервативна, то потенциальные энергии надо приравнять

Отбрасывая малые второго порядка, получаем

49)