
- •События и операции над ними. Относительные частоты и их свойства.
- •2.Аксиомы тв. Дискретное пространство элементарных исходов. Классическое определение вероятности.
- •3. Элементы комбинаторики. Основное правило комбинаторики.
- •(Обобщенная теорема сложения вероятностей)
- •(Теорема сложения k слагаемых)
- •6.Условная вероятность. Независимость.
- •7.Формулы полной вероятности и Байеса.
- •8.Схема Бернулли.Полиноминальное распределение.
- •9.Теорема Пуассона.
- •10.Локальная и интегральная теоремы Муавра-Лапласа.
- •12.Дискретные случайные величины. Закон распределения. Биномиальное, геометрическое и распределение Пуассона.
- •13.Математическое ожидание дискретной случайной величины и его свойства
- •Свойства математического ожидания:
- •Математическое ожидание постоянной величины равно самой постоянной:
- •Постоянный множитель можно выносить за знак математического ожидания:
- •14.Дисперсия случайной величины и ее свойства. Начальный и центральный момент.
- •15. Непрерывные случайные величины. Св-во плотности распределения
- •16. Равномерное, показательное, нормальное распределения и их св-ва
- •17. Лемма о нормальном распределении. Критерии независимости дискретной и непрерывной случайной величин
- •18. Случайный вектор. Св-ва функции распределения случайного вектора
- •2.Функция распределения случайного вектора неубывающая по каждому аргументу.
- •19. Случайный вектор. Свойства плотности распределения случайного вектора
- •20. Функция двух случайных аргументов. Формула свёртки
- •21. Числовые характеристики системы двух случайных величин. Корелляция и ее св-ва
- •22. Задачи математической статистики. Генеральная совокупность. Выборка
- •23. Эмпирическая функция распределения. Полигон и гистограмма
9.Теорема Пуассона.
Теорема.
Пусть производится n
независимые испытания в каждом из
которых событие а малое с событием р
тогда, если число испытании неограниченно
возрастает, а р стремится к нулю и причем
np=a
величина постоянная, то вероятность
появления k
события Р в n
испытаниях находится по формуле
![]() .
.
Доказательство:
По формуле
Бернулли
![]() ,
где q=1-p.
,
где q=1-p.
Отсюда
![]() .
.
По условию
![]() .
.
Подставляя, получим
![]()
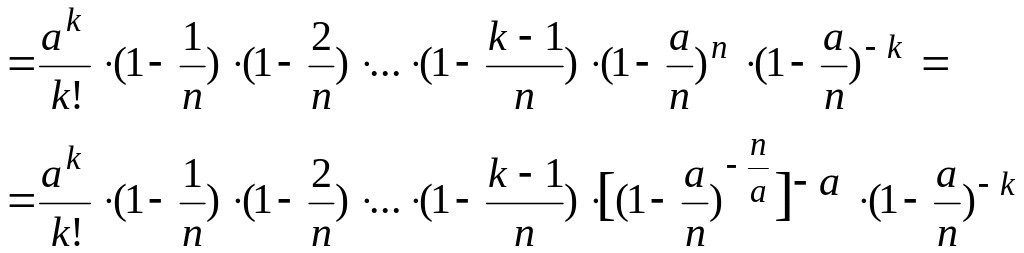
Перейдем к пределу
при
![]() ,
т.е.
,
т.е.
![]()
![]() .
.
![]() —формула
Пуассона.
—формула
Пуассона.
Замечание:
Теоремой удобно пользоваться, когда
р→0,
![]() .
Существуют специальные таблицы, в
которых приведены значения вероятностей
для различных а и k.
.
Существуют специальные таблицы, в
которых приведены значения вероятностей
для различных а и k.
10.Локальная и интегральная теоремы Муавра-Лапласа.
Формулой Бернулли удобно пользоваться, когда значение n не очень велико. Если же n достаточно велико, то удобнее пользоваться приближенными формулами, одна из которых содержится в следующей теореме.
Теорема (локальная теорема Муавра-Лапласа).
Если вероятность появления события А в каждом отдельном испытании постоянная и отлична от 0 и 1, т.е. 0<p<1, то вероятность того, что событие А появится ровно k раз в n независимых испытаниях.
![]() ,
где
,
где
![]() ;
;
![]() ,
q=1-p.
,
q=1-p.
Замечание: Имеются специальные таблицы значений функций φ(х). Нужно учитывать, что функция φ(х)–четная, т.е. φ(х)=φ(-х).
Теорема (интегральная теорема Муавра-Лапласа).
Если вероятность
появления события А в каждом отдельном
испытании постоянна и отлична от 0 и 1,
т.е.0<p<1,
то вероятность того, что событие А
появится от k1
до k2
раз в n
независимых испытаниях определяется
выражением:![]() ,
где
,
где
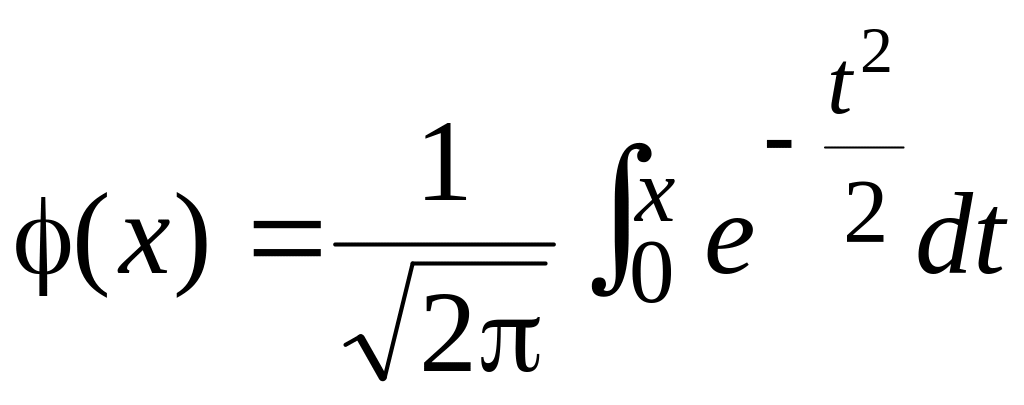 —функция
Лапласа,
—функция
Лапласа,
![]() ,
,
![]() ,
,
![]() .
.
Замечание:
Функция Лапласа—нечетная, т.е.
![]() .
Значения находят по таблице.
.
Значения находят по таблице.
11.Случайные величины. Функция распределения и их свойства.
Случайной величиной Х называется функция X(w), отображающая пространство элементарных исходов Ω во множ-ве действительных чисел R.
Множество значений случайной величины обозначается Ωх. Одной из важных характеристик случайной величины является функция распределения случайной величины.
Функцией распределения случайной величины Х называется функция F(x) действительной переменной х, определяющая вероятность того, что случайная величина Х примет в результате эксперимента значение, меньшее некоторого фиксированного числа х.
![]() .
.
Замечание: Если рассматривать случайную величину Х как случайную точку на оси ох, то функция распределения F(x) с геометрической точки зрения—это вероятность того, что случайная точка Х в результате реализации эксперимента попадет левее точки х.
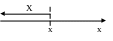
Свойства функции распределения.
Функция распределения F(x)–неубывающая функция, т.е. для
 таких что x1<x2
таких что x1<x2
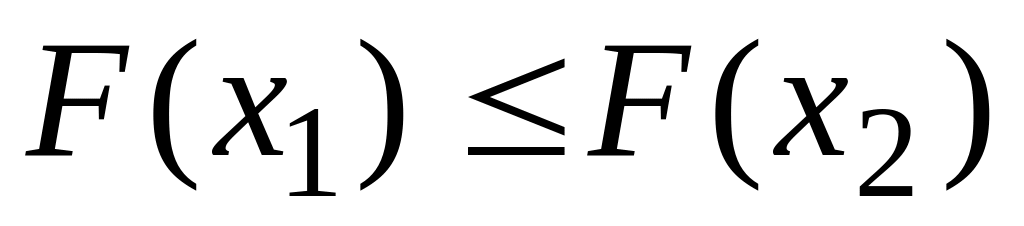 .
.
![]() .
.
![]() ,
т.е.
,
т.е.
![]() .
Поскольку
.
Поскольку
![]() ,
то
,
то
![]() .
.
Для любых
 вероятность того что
вероятность того что
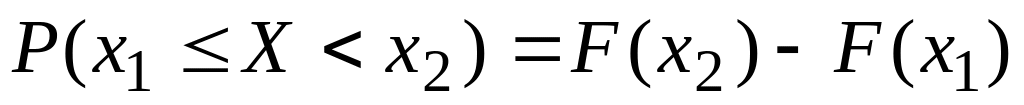
Замечание. Если функция распределения F(x) непрерывная, то свойство выполняется и при замене знаков ≤ и < на < и ≤.
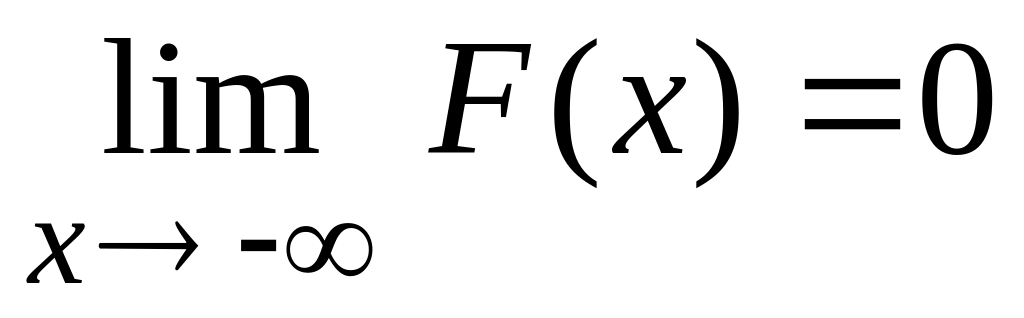 ,
,
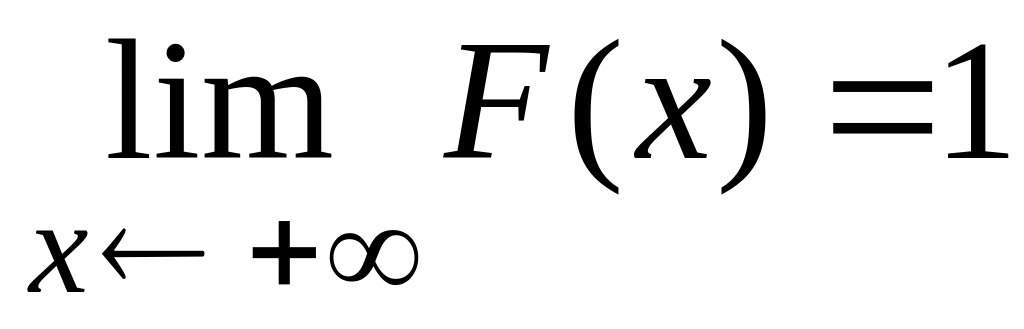 .
.
![]() ,
,
![]() .
.
Функция распределения F(x) непрерывна слева. (т.е.
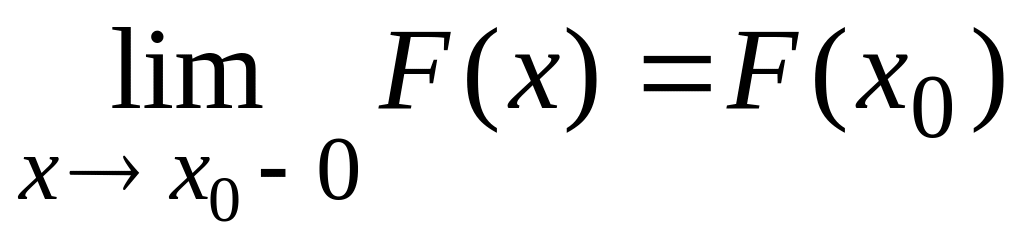 ).
).Вероятность того, что значение случайной величины Х больше некоторого числа х, вычисляется по формуле.
![]() .
.
![]() .
Найдем их вероятности
.
Найдем их вероятности
![]() .
.
Поскольку вероятность достоверного события равна единице, то
![]() .
Отсюда
.
Отсюда
![]() .
.
