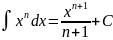42. Таблица неопределенных интегралов
43. Определенный интеграл. Задача о вычислении площади криволинейной трапеции. Геометрический смысл определенного интеграла.
Рассмотрим Криволинейную трапецию ограниченную сверху непрерывной ф-ей y=f(x), f(x)≥0 с боков вертикалями x=a, x=b где b>a, снижу отрезком [a;b] оси OX. Необходимо найти площадь этой криволинейной трапеции.
Разделим отрезок [a;b] точками разделив на элементарные отрезки ∆x1, ∆x2, ∆xn и проведем в точках деления перпендикуляры, прямые до пересечения с графиком ф-ии y=f(x)
На каждом элементарном отрезке выберем точку x и проведем перпендикуляры до y=f(x). В результате получим ступенчатую фигуру, состоящую из прямоугольников высоты f(x) и длины основания ∆x площадь каждого i-прямоугольника S ступенчатой фигуры равна сумме площадей этих прямоугольников
Геометрический смысл определенного интеграла
Очевидно, что при
,
,
Определенный интеграл
равен площади криволинейной трапеции,
ограниченный сверху непрерывной ф-ей
y=f(x),
f(x)≥0 с
боков прямыми x=a,
x=b, b>a
снизу отрезком [a;b]
оси OX
44. Определенный интеграл с переменным верхним пределом
Рассмотрим ф-ию
это Sкриволин трап.
Дадим x приращение ∆x:
x+∆x. Тогда
ф-ия получит приращение ∆Ф
Обозначим через m=min f(x) когда x Є [x; x+∆x], а через M=max f(x), x Є [x; x+∆x]. Тогда точка ∆x ≤∆Ф≤M∆x (1)
Разделим на ∆x
(2)
Очевидно что
т.е. правая и левая части неравенства
(2) имеют одинаковый предел f(x)
тогда по 1-му признаку существованию
предела, но
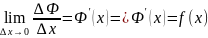
Получается что производная определенного интеграла с переменным верхним пределом равна подынтегральной ф-ии в точке верхнего предела.
45. Связь определенного интеграла с неопределенным. Ф-ла Ньютона-Лейбница. Интеграл с переменным внешним пределом.
имеет производную равную f(x) Ф’(x)=f(x)
Пусть F(x) есть первообразная ф-ии f(x) т.е. F’(x)=f(x) тогда ф-ии Ф(x) и F(x) есть первообразные одной и той же ф-ии f(x) а тогда по следствию 1
Ф(x)=F(x)+C
(3)
Положим в (3) x=a
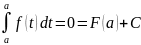
Следовательно C=-F(a)
(4)
Положим в (4) что x=b тогда
(5)
Формула (5) называется формулой Ньютона-Лейбница
Свойство определенного интеграла:
Определенный интеграл не зависит от обозначения переменной т.к. он равен приращению производной
Если пределы определенного интеграла одинаковы то интеграл равен нулю это следует из геометрического смысла определенного интеграла и из формулы Ньютона-Лейбница
Если поменять местами пределы интегрирования то интеграл изменит знак на противоположный
Постоянный множитель можно выносить за знак определенного интеграла
Если ф-ия f(x) непрерывна и интегрируема на [a;b], [a;c], [c;b] то интеграл равен интегралу
И действительно
Отметим что точка c может и не принадлежать отрезку [a;b]
Если ф-ии f(x), g(x), h(x) непрерывны и интегрируемы на [a;b] то
Интеграл от алгебраической суммы равен сумме интегралов от этих ф-ий.
Интегрирование по частям в определенном интеграле.
Известно, что d(uv)=uvd+vdu (7)
Udv=d(uv)-vdu (8)
Проинтегрируем (8) на [a;b] предполагая что ф-ии u(x) и v(x) дифференцируемы на [a;b] ф-ия v(x) интегрируема на [a;b]
(9)
(9) – формула интегрирования по частям в определенном интеграле
Интегрирование подстановкой в определенном интеграле
Рассмотрим
Положим x=φ(t) ф-ия определенная и дифференцируемая на [α;β] причем φ(α)=a,φ(β)=b тогда
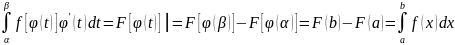
Формула доказана и в одну и в другую сторону
46. Приложение определенного интеграла
S крив трап
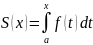
В случае если ф-ия непрерывна положительна и сверху и снизу
П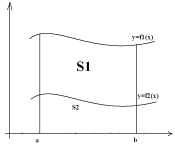
усть
нужно найти S
фигуры ограниченной сверху непрерывной
ф-ей f1(x)
снизу непрерывной f2(x)
и с боков прямыми x=a,
x=b
Тогда
Пусть нужно найти площадь фигуры ограниченной замкнутой непрерывной ф-ей f(x)
Спроектируем на
Разделим фигуру крайней точкой на yв и yн
Е
сли
фигура ориентирована вдоль оси ординат,
то S
лучше вычислять по (10)
(10)
Объем тела
Пусть
некоторое тело ориентировано вдоль
оси OX
в точке x
проведено сечение перпендикулярно оси
OX.
Пусть Sсеч
в точке x
есть непрерывная ф-ия S(x)
Взяв точку x+∆x проведем в этой точке так же сечение S(x+∆x) тогда объем тела расположенного между сечениями S(x) и S(x+∆x) Обозначим ∆v Обозначим
,
xЄ(x;x+∆x)
,
xЄ(x;x+∆x)
Тогда ∆v
(11)
Разделим (11) на ∆x и перейдем в (12) к пределу в котором ∆x→0
Тогда на основании 1-го признака существования предела или теоремы о 2-х милиционерах мы получим
,
но
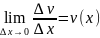следовательно v(x)=S(x)
т.е.
(13)
Найдена формула объема тела через известное поперечное сечение (13). Найдем объем тела, образованного вращением вокруг оси OX криволинейной трапеции
Каждая точка криволинейной трапеции описывает окружность
Объем тела полученного в результате вращения вокруг оси OY криволинейной трапеции
