13 Число е. Второй замечательный предел и его следствия.
E=2,71828…
Рассмотрим
последовательность (1+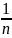
)n
N=1 =>2
N=2 => (3/2)2
Последовательность возрастающая при возрастающем n
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(сочетания)
(1+
)n=1+
*
+
*(
)2+
*(
)3+…+(
)n=1+n*
+
*(
)2+
*(
)3+
*(
)4+…+(
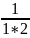)n=1+1+(1-
)*
+(1-
)(1-
)*
+(1-
)(1-
)(1-
)*
+…+(
)n<2+
+
+
+…+
=
+
+
+…+
=
=
=1-
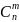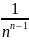<1
2<(1+ )n<3
=e
Следствия
=
15 Теоремы о непрерывных ф-ях. Теорема1,2,3,4
Теорема1.
алгеброическая сумма конечного числа непрерывных ф-ций есть ф-я непрерывная.
Дано.
f(x), g(x), h(x) – непрерывные
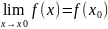
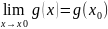
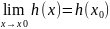
Док-во
f(x)+g(x)-h(x)
Теорема2.
Произведения конечного числа непрерывных функций есть ф-ция непрерывная.
Теорема3.
Частное от деления двух непрерывных ф-ций есть ф-ция непрерывная всюду за исключением корней знаменателя.
Теорема4.
Непрерывная ф-ция от непрерывной ф-ции есть также ф-ция непрерывная т.е. сложная ф-ция состоящая из непрерывных ф-ций есть ф-ция непрерывная.
Дано.
F[φ(x)]
F(u), uє(A;B)
u=φ(x), xє(α;β), E[φ]=(A;B) по замечанию
Т.е. сложная ф-ия f[φ(x0)] непрерывна в точке x0
16 Типы точек разрыва. Устранимый разрыв. Разрывы 1,2 рода. Скачок.
Точка x0 называется точкой устраненного разрыва ф-ии f(x) если односторонние пределы ф-ий в этой точке равны, но не совпадают со значением ф-ии в точке
f(x)
точка x1 разрыва ф-ии f(x) называется точкой разрыва 1-го рода если односторонние пределы ф-ии в этой точке не равны
f(x1-0)≠f(x1+0)
при этом ф-ия не обязательно должна быть определена в точке x1 т.е. f(x1) может и не существовать.
Разность односторонних пределов ф-ий в точке x1 называется скачком ф-ии f(x) в точке x1
α=f(x1+0)-f(x1-0)
напр.:
f(x)=
точка x2 ф-ии f(x) называется точкой разрыва второго рода если хотя бы один из односторонних пределов этой точки не существует или бесконечен.
F(x)=
;
Если предел и слева и справа существуют, равны между собой и совпадают со значением ф-ии в точке то ф-ия f(x) непрерывна в данной точке
17 Производная. Геометрический и механический смысл. Уравнение касательной.
Рассмотрим ф-ию y=f(x), xє(a;b) конечного или бесконечного, дадим x приращение Δx. Составим приращение ф-ии Δy=f(x+Δx)-f(x), (x+Δx)є(a;b).
Рассмотрим
отношение
.
Оно показывает во сколько раз Δy>Δx
т.е. дает среднюю скорость изменения y
относительно x на промежутке
[x;x+Δx].
Формула
y’=
определяет ф-ию f(x)
которая носит название производной
f’(x).
Таким образом производной ф-ии называется предел (если он существует) приращения ф-ии к приращению аргумента, когда приращение аргумента →0.
Ф-ия имеющая производную в каждой точке некоторого множества называется дифференцируемой на этом множестве.
y’(x)=f’(x)=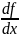
=
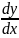
f’(x)=f’(x0),
геометрический смысл производной. Задача о касательной.
Найти уравнение касательной в некоторой точке M зная уравнение непрерывно дифференцируемой ф-ии y=f(x)
Пусть на некоторой кривой l взяты точки L и L1 и проведена секущая MM1.
Предельное положение секущей MM1 когда точка M1 движется по кривой l неограниченно приближаясь к точке M называется касательной.
Если секущая MM1 когда M1→M не имеет предельного положения то говорят что касательная в данной точке M не существует
A(x;f(x))
B(x+Δx;f(x+Δx))
AC=Δx, BC=Δy
На кривой взяты точки A и B, проведена секущая AB. Секущая AB образует угол φ с осью OX, OT – касательная к кривой в точке A образует угол α
Kкас - угловой коэффициент к касательной
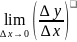=y’(x)
=>y’(x)=
Kкас
т.е. Kкас к графику ф-ии = значению производной в точке касания.
Зная Kкас можно написать ее уравнение
Y-y=f’(x)(X-x)
Механический смысл производной.
Пусть точка M движется по оси OX и каждому значению времени t соответствует некоторое расстояние OM=OX значит X есть ф-ия от t. Пусть в момент времени t+Δt точка занимает некоторое положение M1 расстояние обозначим x(t+Δt)=OM1 тогда за промежуток времени Δt точка проходит расстояние Δx=x(t+Δt)-x(t)
Отношение
=
=
vср есть средняя
скорость изменения x за
время Δt.
Предел средней скорости движения при Δt→0 называется скоростью движения в данный момент. Таким образом v прямолинейного движения = производной от пути по времени.