
- •31. Бесконечно малые функции.
- •32 Основные теоремы о пределах.
- •33. Первый замечательный предел (с выводом).
- •34. Второй замечательный предел.
- •36. Непрерывность функции в точке.
- •37. Точки разрыва, их классификация.
- •39. Определение и геометрический смысл производной.
- •40. Дифференцируемость и непрерывность.
- •43. Производные функций: логарифм, показательная функция, стеленная.
- •44. Логарифмическое дифференцирование, дифференцирование неявных функций.
- •63. Производная по направлению.
- •64. Градиент.
40. Дифференцируемость и непрерывность.
Непрерывность функции есть необходимое условие ля ее дифференцируемости.
Функция y=f(x) называется дифференцируемой в
некоторой точке x0,
если она имеет в этой точке определенную
производную, т.е. если предел
отношения ![]() существует
и конечен.
существует
и конечен.
Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что онадифференцируема на отрезке [а; b] или соответственно в интервале (а; b).
Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.
Теорема. Если функция y=f(x) дифференцируема в некоторой точке x0, то она в этой точке непрерывна.
Таким образом,из дифференцируемости функции следует ее непрерывность.
41.Основные правила дифференцирования
Пусть ![]() ,
тогда:
,
тогда:

7)
Если ![]() ,
то есть
,
то есть ![]() ,
где
,
где ![]() и
и ![]() имеют
производные, то
имеют
производные, то ![]() (правило
дифференцирования сложной функции).
(правило
дифференцирования сложной функции).
42. Производные функций: синуса, тангенса и обратных тригонометрических.

43. Производные функций: логарифм, показательная функция, стеленная.
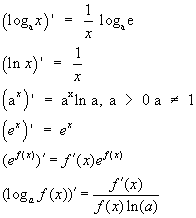

44. Логарифмическое дифференцирование, дифференцирование неявных функций.
Логарифмическое дифференцирование |
||||||||||||||||||||||||
|
||||||||||||||||||||||||
Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием позволяет эффективно вычислять производные степенных и рациональных функций. Рассмотрим этот подход более детально. Пусть дана функция y = f(x). Возьмем натуральные логарифмы от обеих частей:
Теперь продифференцируем это выражение как сложную функцию, имея ввиду, что y - это функция от x.
Неявно заданная функция: Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2у-х+у=0).Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.Производная неявной функции выражается через аргумент х и функцию у.
45 Дифференциал, его применение в приближенных вычислениях.
Дифференциалом dy
функции y=y(x) называется главная часть
ее приращения, пропорциональная
приращению Применение дифференциала в приближенных вычислениях.
Теорема о производной сложной функции (дифференцирование сложной функции). Пусть x=x(t), y=y(t) – дифференцируемы в точке t, z=f(x,y) – дифференцируема в точке t(x,y), если t получит Δt, то x получит Δx, y – Δy, z –Δz, а т.к. функция z дифференцируема, то ее приращение
46. Геометрический смысл и свойства дифференциала Геометрический смысл: дифференциал функции f(x), соответствующей данным значениям x и Δx, равен приращению ординаты касательной к кривой y=f(x) в данной точке х. Дифференциал функции обладает свойствами:
Следствие. Если две дифференцируемые функции отличаются постоянным слагаемым, то их дифференциалы равны d(u+c) = du (c= const).
Следствие. Постоянный множитель можно выносить за знак дифференциала d(cu) = cdu (с = const).
47. Производные и дифференциалы высших порядков Пусть производная некоторой функции f дифференцируема. Тогда производная от производной этой функции называется второй производной функции fи обозначается f". Таким образом, f"(x) = (f'(x))'. Если дифференцируема (n - 1)-я производная функции f, то ее n-й производной называется производная от (n - 1)-й производной функции f и обозначается f(n). Итак, f(n)(x) = (f(n-1)(x))', n ϵ N, f(0)(x) = f(x). Число n называется порядком производной. Дифференциалом n-го порядка функции f называется дифференциал от дифференциала (n - 1)-го порядка этой же функции. Таким образом, dnf(x) = d(dn-1f(x)), d0f(x) = f(x), n ϵ N. Если x - независимая переменная, то dx = const и d2x = d3x = ... = dnx = 0. В этом случае справедлива формула dnf(x) = f(n)(x)(dx)n. 48. Функция, заданная параметрически Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений
где t — вспомогательная переменная, называемая параметром. Найдем производную у'х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции
Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у'х=y't•t'x. С учетом равенства (21.2) получаем
Полученная формула позволяет находить производную у'х от функции заданной параметрически, не находя непосредственной зависимости у от х.
49. Интервалы монотонности. Монотонность функции. Условия монотонности. Оказывается, монотонность функции связана с тем, каков знак ее производной:
50. Экстремумы (необходимое условие существования с док.). Определение. Точка x0 называется точкой минимума функции f, если для всех x из некоторой окрестности x0 выполняется неравенство f(x) ≥ f(x0. Определение. Точка x0 называется точкой максимума функции f, если для всех x из некоторой окрестности x0 выполняется неравенство f(x) ≤ f(x0.Для точек минимума и максимума функции есть общее определение - точки экстремума. Значение функции в этих точках соответственно назыветсямаксимумом или минимумом этой функции. Общее название - экстремум функции. Точки максимума обычно обозначают xmax, а точки минимума - xminДоказательство. Докажем необходимость условия существования максимума. Пусть f '(x) = 0, f ''(x) > 0. Так как f ''(x) непрерывна, то в достаточно малом интервале (x0 - h, x0 + h) вторая производная положительна: f ''(x) > 0. Это означает, что f '(x) возрастает в этом интервале. Так как при этом f '(x0 )=0, то f '(x)<0 в интервале (x0 - h, x0 ) и f '(x)>0 в интервале (x0 , x0 + h). Таким образом, функция f(x) убывает в интервале (x0 - h, x0 ) и возрастает в интервале (x0 , x0 + h). Поэтому в точке x0 функция f(x) имеет минимум. Аналогично доказывается достаточность условия существования максимума. На рисунке функция f(x) имеет в точке x1 минимум, в точке x2 - максимум. Второй производной можно воспользоваться при решении задач на отыскание максимума и минимума функции.
51. Экстремумы (достаточное условие существования без док.), схема исследования на экстремум Теорема 1.Если функция f(x) имеет в каждой точке интервала (a, b) неотрицательную производную, то она является неубывающей функцией в этом интервале. Теорема 2. Если функция f(x) в каждой точке интервала (a, b) имеет неположительную производную, то она является невозрастающей функцией в этом интервале. Теорема 3. (первый достаточный признак экстремума). Если производная f '(x) функции f(x) обращается в нуль в точке x0 или не существует и при переходе через x0 меняет свой знак, то функция f(x) имеет в этой точке экстремум (максимум, если знак меняется с "+" на "-", и минимум, если знак меняется с "-" на "+"). Теорема 4. (второй достаточный признак существования экстремума функции). Если в точке x0 первая производная f '(x) функции f(x) обращается в нуль, а её вторая производная f ''(x) отлична от нуля, то в точке x0 функция f(x) достигает экстремума (минимума, если f ''(x) > 0, и максимума, если f ''(x) < 0). Предполагается, что f ''(x) непрерывна в точке x0 и ее окрестности. Алгоритм исследования функции на экстремум: 1)Найти производную функции. 2)Найти критические точки, т.е. точки, в которых функция непрерывна, а производная равна нулю или не существует. 3)Рассмотреть окрестность каждой из точек, и исследовать знак производной слева и справа от этой точки. 4)Определить координаты экстремальных точек, для этого значения критических точек подставить в данную функцию. Используя достаточные условия экстремума, сделать соответствующие выводы. 52. Интервалы выпуклости и вогнутости, точки перегиба.
График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале. График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале. Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый. Теорема. Пусть кривая определяется уравнением y = f(x). Если f ''(x0) = 0 или f ''(x0) не существует и при переходе через значение x = x0 производная f ''(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба.
53. Асимптоты. Прямая называется асимптотой графика функции y = f(x), если расстояние от переменной точки M графика до этой прямой при удалении точки M в бесконечность стремится к нулю, т.е. точка графика функции при своем стремлении в бесконечность должна неограниченно приближаться к асимптоте. вертикальной асимптотой графика функции y = f(x) называется прямая, если f(x) → ∞ хотя бы при одном из условий x→ x0 – 0 или x → x0 + 0, x = x0 Следовательно, для отыскания вертикальных асимптот графика функции y = f(x) нужно найти те значения x = x0, при которых функция обращается в бесконечность (терпит бесконечный разрыв). Тогда вертикальная асимптота имеет уравнение x = x0.
Теорема.
Прямая y = kx + b служит
наклонной
асимптотой
при x →
+∞ для графика функции y = f(x) тогда
и только тогда, когда 54.Формула Тейлора:
(Rn(x) - остаточный член формулы Тейлора). Многочлен Тейлора порядка n:
Остаточный член формулы Тейлора В форме Лагранжа:
В форме Коши:
В форме Пеано:
В интегральной форме:
55. Формула Тейлора для любой функции, разложение функций ex, sinx. Основные разложения в ряд Тейлора
56. Функции многих переменных: способы задания, область определения, непрерывность и разрывы.
1. Обозначим через D некоторое множество точек в п-мерном пространстве. Если задан закон f , в силу которого каждой точке М(х;...;х) D ставится в соответствие число и, то говорят, что на множестве D определена функция и= f(х;...;х). Множество точек М(х;...;х), для которых функция и= f(х;...;х) определена, называют областью определения этой функции и обозначают D(f). Функции многих переменных можно обозначать одним символом и=f(М), указывая размерность пространства, которому принадлежит точка М. Функции двух переменных можно изобразить графически в виде некоторой поверхности. Графиком функции двух переменных z=f(х;у) в прямоугольной системе координат Оху называется геометрическое место точек в трехмерном пространстве, координаты которых (х;у;z) удовлетворяют уравнению z=f(х;у). Функция и=f(М) называется непрерывной в точке М, если = f(М). Функция и=f(М) называется непрерывной на множестве D, если она непрерывна в каждой точке МD. Точки, в которых непрерывность функции нарушается, называются точками разрыва функция. Точки разрыва могут быть изолированными, создавать линии разрыва, поверхности разрыва и т. д. Например, функция z= имеет разрыв в точке (0;0), а функция z= имеет разрыв на параболе
57. Частные производные, геометрический смысл.
Частной
производной функции
z=z(x, y) по аргументe x называется
производная этой функции по x при
постоянном y. Аналогично, частной
производной функции z=z(x, y) по аргументу
y называется производная этой
функции по y при постоянном x. Частные
производные обозначаются следующим
образом:
Геометрически дифференцируемость функции в точке означает наличие определённой касательной в точке. 58. Полный дифференциал, его применение для приближенных вычислений.
Теорема об инвариантности полного дифференциала (инвариантность формы полного дифференциала).
Форма
дифференциала не изменится,
если x и y будут функциями
новых переменных U и V:
Полный
дифференциал,
функции f (x,
у, z,...)
нескольких независимых переменных
— выражение
59. Дифференцирование сложной функции.
Правило дифференцирования сложной функции
Сложная
функция (композиция
функций, суперпозиция
функций)
обозначается Производная композиции равна:
Если необходимо взять производную от композиции трех и более функций, то последовательно применяем указанное выше правило. Например,
60. Дифференцирование неявных функций. Дифференцирование неявной функции Функция z = ƒ (х; у) называется неявной, если она задается уравнением
неразрешенным
относительно z. Найдем частные
производные
откуда
61. Экстремум функции двух переменных
Говорят,
что функция
Говорят,
что функция
имеет минимум в
точке
,
т.е. при
,
если Максимум и минимум функции называются экстремумами функции.
Теорема (необходимое
условие экстремума функции двух
переменных). Если функция
достигает
экстремума при
,
то каждая частная производная первого
порядка от
Теорема (достаточное
условие экстремума функции двух
переменных). Пусть в некоторой области,
содержащей точку
функция
имеет
непрерывные частные производные до
третьего порядка включительно. Пусть,
кроме того, точка
является
критической точкой функции 62. Метод наименьших квадратов. Такая модель в общем виде может быть представлена уравнением (1.2): yt = a0 + a1 х1t +...+ an хnt + εt . Исходными данными при оценке параметров a0 , a1 ,..., an является вектор значений зависимой переменной y = (y1 , y2 , ... , yT)' и матрица значений независимых переменных
в
которой первый столбец, состоящий из
единиц, соответствует коэффициенту
модели Название свое метод наименьших квадратов получил, исходя из основного принципа, которому должны удовлетворять полученные на его основе оценки параметров: сумма квадратов ошибки модели должна быть минимальной.
|
|
|||||||||||||||||||||||

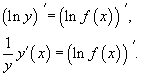 Отсюда
видно, что искомая производная равна
Отсюда
видно, что искомая производная равна
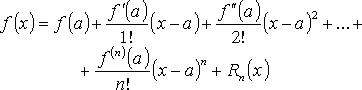

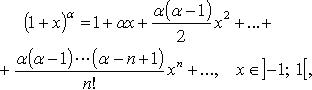



 ,
тогда
при
:
1)
имеет
максимум, если дискриминант
,
тогда
при
:
1)
имеет
максимум, если дискриминант  ;
2)
имеет
минимум, если дискриминант
и
;
2)
имеет
минимум, если дискриминант
и 