31. Бесконечно малые функции.
Определение.
Функция f(x)
называется бесконечно
малой при
ха,
где а может быть числом или одной из
величин ,
+ или
-,
если 
.
Бесконечно малой функция может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет.
Пример. Функция f(x)
= xn является
бесконечно малой при х0
и не является бесконечно малой при х1,
т.к. 
.
Теорема. Для того, чтобы функция f(x) при ха имела предел, равный А, необходимо и достаточно, чтобы вблизи точки х = а выполнялось условие
f(x) = A + (x),
где (х) – бесконечно малая при х а ((х)0 при х а).
Свойства бесконечно малых функций:
Сумма фиксированного числа бесконечно малых функций при ха тоже бесконечно
малая функция при ха.
2) Произведение фиксированного числа бесконечно малых функций при ха тоже бесконечно малая функция при ха.
3) Произведение бесконечно малой функции на функцию, ограниченную вблизи точки х = а является бесконечно малой функцией при ха.
4) Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю есть величина бесконечно малая.
32 Основные теоремы о пределах.
.
Теорема 2. Если
функции f(x)
и g(x)
имеют пределы в точке 
,
то:
1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.
(2)
2) предел произведения функций равен произведению пределов сомножителей, т.е.
(3)
3)предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.е.
(4)
Замечание. Формулы (2) и (3) справедливы для любого конечного числа функций.
Следствие
1. Предел
постоянной равен самой постоянной,
т.е.
Следствие
2. Постоянный
множитель можно выносить за знак предела,
т.е.
Теорема
3 (о
пределе сложной функции). Если
существует конечный предел
а
функция f(u) непрерывна в точке 
,
то
Другими словами, для непрерывных функций символы предела и функции можно поменять местами.
33. Первый замечательный предел (с выводом).
Первый замечательный предел: Главное, что Х стремится к 0.
Следствия
Из первого замечательного предела следует эквивалентность при х →0 следующих бесконечно малых величин: ах, sinax; tgax; arcsinax; arctgax. Это означает, что предел отношения двух любых из этих функций при х →0 равен 1.
С помощью этого соотношения можно вычислить массу других неопределенностей, которые без применения первого замечательного предела вычислялись бы сложнее.
34. Второй замечательный предел.
Второй замечательный предел: Главное, что Х стремится к бесконечности.
или
Следствия:
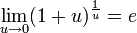
для 
, 
35. Сравнение бесконечно малых, эквивалентные б.м.
Определение
1.
Функции 
и 
называются
бесконечно малыми величинами одного
порядка малости, если 
.
Определение
2. Функция
называется
бесконечно малой величиной более
высокого порядка малости, чем
,
если 
.
Определение
3.
Функция
называется
бесконечно малой величиной более низкого
порядка малости, чем
,
если 
.
Тот
факт, что
,
например, имеет более высокий порядок
малости, чем
,
можно обозначить следующим образом: 
.
Определение
4.Функции
и
называются
несравнимыми бесконечно малыми
величинами, если 
не
существует и не равен 
.
Если 
то
α и ß называются эквивалентными
бесконечно малыми (при
х→x0);
это обозначается так: α~ß.
Теорема 1. Предел отношения двух бесконечно малых функций не изменится, если каждую или одну из них заменить эквивалентной ей бесконечно малой.
Теорема 2. Разность двух эквивалентных бесконечно малых функций есть бесконечно малая более высокого порядка, чем каждая из них.
Справедливо и обратное утверждение: если разность б.м.ф. α и ß есть бесконечно малая высшего порядка, чем α или ß, то α и ß — эквивалентные бесконечно малые.
Теорема 3. Сумма конечного числа бесконечно малых функций разных порядков эквивалентна слагаемому низшего порядка.
Замена суммы б.м.ф. ее главной частью называется отбрасыванием бесконечно малых высшего порядка.