
- •6. Работа, мощность, энергия
- •7. Кинетическая и потенциальная энергия
- •Формы записи закона сохранения энергии в классической физике
- •Расширенная форма записи закона сохранения энергии
- •9. Закон сохранения импульса.
- •11. Удар абсолютно упругих и неупругих тел
- •12. Момент импульса
- •14. Момент инерции
- •14.1 Теорема Штейнера
- •15. Кинетическая энергия вращения
- •16. Момент импульса. Тензор инерции.
- •17. Свободные оси. Гироскоп
- •18. Деформация твердого тела
- •19. Неинерциальные системы отсчета и силы инерции
15. Кинетическая энергия вращения
Возьмем абсолютно твердое тело, вращающееся около неподвижной оси z, проходящей через него (рис. 1). Разобьем тело на маленькие объемы с элементарными массами m1, m2,..., mn , находящиеся на расстоянии r1, r2,..., rn от оси.
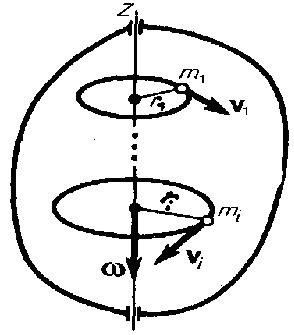
Рис.1
При
вращении твердого тела относительно
неподвижной оси каждый из его элементарных
объемов массами mi опишет
окружность соответствующих радиусов
ri;
при этом объем будет иметь соответствующую
линейную скорость vi.
Но так как мы рассматриваем абсолютно
твердое тело, то угловая скорость
вращения этих объемов
одинакова: ![]() (1) Кинетическую
энергию вращающегося тела найдем как
сумму кинетических энергий его
элементарных объемов:
(1) Кинетическую
энергию вращающегося тела найдем как
сумму кинетических энергий его
элементарных объемов:  или
Используя
выражение (1), получаем
или
Используя
выражение (1), получаем ![]() где
Jz -
момент инерции тела относительно оси
z. Таким образом, кинетическая энергия
вращающегося тела
где
Jz -
момент инерции тела относительно оси
z. Таким образом, кинетическая энергия
вращающегося тела ![]() (2) Из
сравнения формулы (2) с выражением для
кинетической энергии поступательно
движущегося тела (T=mv2/2),
мы видим, что момент инерции является
мерой инертности тела при вращательном
движении. Формула (2) справедлива для
тела вращающегося вокруг неподвижной
оси.В качеcтве примера напишем формулу
для плоского движения тела, например
цилиндра, скатывающегося с наклонной
плоскости без скольжения. Его энергия
движения складывается из энергии
поступательного движения и энергии
вращения:
(2) Из
сравнения формулы (2) с выражением для
кинетической энергии поступательно
движущегося тела (T=mv2/2),
мы видим, что момент инерции является
мерой инертности тела при вращательном
движении. Формула (2) справедлива для
тела вращающегося вокруг неподвижной
оси.В качеcтве примера напишем формулу
для плоского движения тела, например
цилиндра, скатывающегося с наклонной
плоскости без скольжения. Его энергия
движения складывается из энергии
поступательного движения и энергии
вращения: ![]() где
m - масса катящегося тела; vc -
скорость центра масс тела; Jc -
момент инерции тела относительно оси,
проходящей через его центр масс; ω -
угловая скорость тела.
где
m - масса катящегося тела; vc -
скорость центра масс тела; Jc -
момент инерции тела относительно оси,
проходящей через его центр масс; ω -
угловая скорость тела.
16. Момент импульса. Тензор инерции.
Момент импульса тела
относительно неподвижной точки -
важнейшее понятие в динамике вращательного
движения твердого тела. Он определяется
так же, как и для системы материальных
точек:
![]() (2.1)
Здесь
(2.1)
Здесь ![]() -
импульс элементарной
-
импульс элементарной ![]() в
лабораторной системе XYZ, а
в
лабораторной системе XYZ, а ![]() -
радиус-вектор массы
с
началом в той неподвижной точке,
относительно которой вычисляется
момент импульса тела.С учетом постоянства
расстояний между точками абсолютно
твердого тела вектор момента
импульса L удается
связать с вектором угловой
скорости
-
радиус-вектор массы
с
началом в той неподвижной точке,
относительно которой вычисляется
момент импульса тела.С учетом постоянства
расстояний между точками абсолютно
твердого тела вектор момента
импульса L удается
связать с вектором угловой
скорости ![]() Рассмотрим,
к примеру, две одинаковые точечные
массы
Рассмотрим,
к примеру, две одинаковые точечные
массы ![]() укрепленные
на концах невесомого стержня АВ (рис.
2.В). Стержень с массами вращается с
угловой скоростью
укрепленные
на концах невесомого стержня АВ (рис.
2.В). Стержень с массами вращается с
угловой скоростью ![]() вокруг
вертикальной оси, проходящей через
середину стержня и перпендикулярной
ему. В этом случае
вокруг
вертикальной оси, проходящей через
середину стержня и перпендикулярной
ему. В этом случае![]() (2.2)Здесь
учтено, что
(2.2)Здесь
учтено, что ![]() а
а ![]()
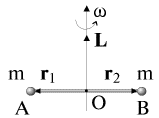 Рис. 2.3.Существенно,
что в этом примере вектор L,
направлен так же, как и
К
сожалению, так бывает не всегда. В этом
можно убедиться на примере, показанном
на рис. 2.4. Здесь невесомый стержень АВ
с двумя массами
Рис. 2.3.Существенно,
что в этом примере вектор L,
направлен так же, как и
К
сожалению, так бывает не всегда. В этом
можно убедиться на примере, показанном
на рис. 2.4. Здесь невесомый стержень АВ
с двумя массами ![]() на
концах жестко закреплен на вертикальной
оси (в точке О) под некоторым углом
на
концах жестко закреплен на вертикальной
оси (в точке О) под некоторым углом ![]() к
ней и лежит в плоскости Oyz. При вращении
стержня вокруг вертикальной оси с
угловой скоростью
вектор L,
определенный по (2.1), будет находиться
в плоскости Oyz и составит угол
к
ней и лежит в плоскости Oyz. При вращении
стержня вокруг вертикальной оси с
угловой скоростью
вектор L,
определенный по (2.1), будет находиться
в плоскости Oyz и составит угол ![]() с
осью z. Система xyz, введенная в начале
лекции 1, жестко связана со стержнем и
поворачивается вместе с ним. При этом
вектор Lостается
в плоскости Oyz, а в лабораторной системе
движется по конической поверхности с
углом полураствора
с
осью z. Система xyz, введенная в начале
лекции 1, жестко связана со стержнем и
поворачивается вместе с ним. При этом
вектор Lостается
в плоскости Oyz, а в лабораторной системе
движется по конической поверхности с
углом полураствора
 Рис. 2.4.Получим
выражение для L в
случае твердого тела произвольной
формы, закрепленного в некоторой точке
О.Пусть
-
радиус-вектор элементарной массы
твердого
тела, а
-
угловая скорость. Тогда
Рис. 2.4.Получим
выражение для L в
случае твердого тела произвольной
формы, закрепленного в некоторой точке
О.Пусть
-
радиус-вектор элементарной массы
твердого
тела, а
-
угловая скорость. Тогда
 (2.3)
(2.3)
Векторы ![]() и L можно
проектировать как на оси лабораторной
системы XYZ, так и на оси системы xyz, жестко
связанной с твердым телом (поскольку
точка О неподвижна, начала обеих систем
можно совместить). Преимущество системы
xyz заключается в том, что в ней
проекции
являются
постоянными величинами (в системе XYZ
они зависят от времени), и выражения
для компонент L,
оказываются проще.
и L можно
проектировать как на оси лабораторной
системы XYZ, так и на оси системы xyz, жестко
связанной с твердым телом (поскольку
точка О неподвижна, начала обеих систем
можно совместить). Преимущество системы
xyz заключается в том, что в ней
проекции
являются
постоянными величинами (в системе XYZ
они зависят от времени), и выражения
для компонент L,
оказываются проще.
Итак, в системе xyz![]() (2.4)Тогда,
продолжая (2.3), можно записать:
(2.4)Тогда,
продолжая (2.3), можно записать:
![]() (2.5)Выражения
для проекций
момента импульса на
оси системы xyz запишем в следующем виде:
(2.5)Выражения
для проекций
момента импульса на
оси системы xyz запишем в следующем виде:
![]() (2.6)
(2.6)
![]() (2.7)
(2.7)
![]() (2.8)
(2.8)
Или
![]() (2.9)
(2.9)
![]() (2.10)
(2.10)
![]() (2.11)
(2.11)
где ![]() -
9 компонент так называемого тензора
инерции
-
9 компонент так называемого тензора
инерции ![]() твердого
тела относительно точки О:
твердого
тела относительно точки О:
 (2.)Диагональные
элементы тензора
(2.)Диагональные
элементы тензора ![]() называются
осевыми моментами инерции, недиагональные
элементы
называются
осевыми моментами инерции, недиагональные
элементы ![]() называются
центробежными моментами инерции.
Обратим внимание, что
называются
центробежными моментами инерции.
Обратим внимание, что ![]() Такой
тензор называют симметричным.
Такой
тензор называют симметричным.
Если
координатам x, y и z присвоить номера 1,
2 и 3 соответственно, то (2.9-2.11) можно
представить в виде (2.13)В
символическом виде можно записать так:
(2.13)В
символическом виде можно записать так:
![]() (2.14)Самое
главное, что стоит за приведенными выше
формулами, заключается в следующем.
Девять величин
(2.14)Самое
главное, что стоит за приведенными выше
формулами, заключается в следующем.
Девять величин ![]() (из
них шесть независимых) определяют
однозначную связь между L и
(из
них шесть независимых) определяют
однозначную связь между L и ![]() причем
оказывается, что L,
вообще говоря, не совпадает по направлению
с
(рис.
2.5)
причем
оказывается, что L,
вообще говоря, не совпадает по направлению
с
(рис.
2.5)
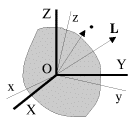 Рис. 2.5.Итак, мы столкнулись
с новым типом величин, имеющим важное
значение в физике - тензором. Если для
задания скалярной величины необходимо
одно число (значение скалярной величины),
векторной - три числа (три проекции
вектора на оси декартовой системы
координат), то для задания тензора
необходимы в общем случае 9 чисел. На
языке математики тензор -
это многокомпонентная величина,
характеризующаяся определенным
поведением при преобразованиях системы
координат (в данном случае компоненты
тензора инерции преобразуются как
произведения соответствующих координат).
Рис. 2.5.Итак, мы столкнулись
с новым типом величин, имеющим важное
значение в физике - тензором. Если для
задания скалярной величины необходимо
одно число (значение скалярной величины),
векторной - три числа (три проекции
вектора на оси декартовой системы
координат), то для задания тензора
необходимы в общем случае 9 чисел. На
языке математики тензор -
это многокомпонентная величина,
характеризующаяся определенным
поведением при преобразованиях системы
координат (в данном случае компоненты
тензора инерции преобразуются как
произведения соответствующих координат).
